Game theory models the behaviors that emerge in situations of conflict, and predicts how rational individuals driven by selfish motivations compete and cooperate. The predicted outcomes can be disappointing. PD, the Prisoner's Dilemma, is a prototypical model in game theory used to demonstrate that the interaction of two rational individuals each attempting to optimize their gains can lead to outcomes that are bad for both participants. So we observe the counterintuitive result of rational individuals knowingly taking decisions that can be predicted to led to poor results.
Countless authors have argued this game-theoretical result being wrong. They challenge the assumption that human beings can be modeled as narrowly rational and selfish individuals. Altruism, evolutionary driven cooperative behaviors, and mystical concepts like super-rationality are put forward as missing features in game theory.
Interestingly, when PD-type results emerge in multiplayer games, such criticism tends to be absent. Silence descends over the 'super-rationality preachers'. The very same people who argue against the outcomes of PD do seem to recognize their own behaviors in the outcomes of what are games that are arguably closer to the reality of situations of conflict and cooperation arising in our societies. Yet, both the multi-player versions and the two-player PD make identical counterintuitive predictions: rational players seek an equilibrium of outcomes that can make every participant being worse off.
What do you do when you recognize your own selfish behaviors in the non-cooperative outcomes of a model, and yet you believe humans capable of behaviors transcending selfishness? Right. You scratch your head and announce you have stumbled on a genuine paradox. So while the two- player game PD is labelled a dilemma, a multiplayer game yielding a similar outcome is labelled a paradox.
Welcome to Braess' paradox, the non-paradoxical multiplayer version of PD.
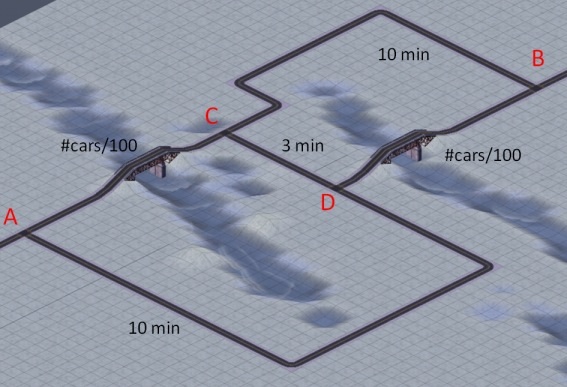
Each morning at rush hour a total of 600 commuters drive their cars from point A to point B. All drivers are rational individuals eager to minimize their own travel time. The road sections AD, CB and CD are so capacious that the travel time on them is independent of the number of cars. The sections AD, and CB always take 10 minutes, and the short stretch CD takes no more than 3 minutes. The bridges, however, cause real bottlenecks, and the time it taken to traverse AC or DB varies in proportion to the number of cars taking that route. If N is the number of cars passing a bridge at rush hour, then the time to cross the section with this bridge is N/100 minutes.
Given all these figures, each morning each individual driver decides on the route to take from A to B. The outcome of all deliberations is a repetitive treadmill like behavior. Each morning all 600 commuters crowd the route ACDB and patiently await the traffic jam at both bridges to resolve. The net result is a total travel time of 600/100 + 3 + 600/100 = 15 minutes for each of them.
Does this make sense?
At this stage you may want to pause and consider the route options. If you would be one of the 600 commuters, would you join the 599 others in following route ACDB?
Of course you would.
Neither you nor any of the other drivers is tempted to take an alternative route like ACB or ADB. These routes would take you 600/100 + 10 = 16 minutes, a full minute longer than the preferred route ACDB.
So each morning you and 599 other commuters travel along route ACDB and patiently queue up at both bridges. Everyone is happy, until one day it is announced that the next day the road stretch CD will be closed for maintenance work. This announcement is the talk of the day. There is no doubt in anyone's mind that this planned closure will create havoc. Would section AD or CB be closed, it would have no impact as these are idle roads. But section CD is used by each and every commuter. Clearly a poorly planned maintenance scheduling, a closure of such a busy section should never coincide with rush hour traffic!
The next morning all 600 commuters enter their cars with a deep sigh, expecting the worst. Each of them randomly selects between the equivalent routes ACB and ADB. The result is that the 600 cars split roughly 50:50 over both routes, and that both bridges carry some 300 cars. Much to everyone's surprise all cars reach point B in no more than 300/100 + 10 = 13 minutes. Two minutes faster than the route ACDB preferred by all drivers.
How can this be? If a group of rational individuals each optimize their own results, how can it be that all of them are better off when their individual choices are being restricted? How can it be that people knowingly make choices that can be predicted to lead to outcomes that are bad for everyone?
Asking these questions is admitting to the wishful thinking that competitive optimization should lead to an optimum. Such is not the case, competitive optimization leads to an equilibrium and not to an optimum. If you think about this, it will become clear there is nothing paradoxical to this assertion. Rather, it would be highly surprising if competitive optimization would invariably lead to optimum outcomes.
A question to test your understanding of the situation: what do you think will happen the day section CD gets opened again? Would all players avoid the section CD and stick to the 50:50 split over routes ACB and ADB, a choice better for all of them?
If all others would do that, that would be great. It would give you the opportunity to follow route ACDB and arrive at B in a record time of about 9 minutes (300/100 + 3 + 301/100 minutes to be precise). But of course all other rational drivers will reason the same. So you will find yourself with 599 others again spending 15 minutes on the route ACDB, without any of you being tempted to select an alternative, yet all of you hoping that damn attractive shortcut between C and D to get closed again.





Comments