The only way around the problem is to use other geometrical shapes to fill in the gaps, a principal used by the builders of mosques as long ago as the 15th century. The complex ornamental structure was "rediscovered“ by mathematicians last century.
Roger Penrose demonstrated a pattern named the Penrose Parquet, which achieves complete coverage following simple rules using two periodically repeating geometrical forms.
Chemists are faced with a similar problem, since, by analogy, molecules with five-fold symmetry cannot completely cover a surface without leaving gaps. Despite this, they strive to pack themselves together in crystals or on surfaces as densely as possible, as do other molecules.
The question is, how do they do it?

Example of the structure of corannulene pentamethyl derivatives: the black atoms show the lattice with regular, six-fold symmetry, between which the molecules with five-fold symmetry “jostle” for space.
Corannulene – bowl-shaped fragments of buckyballs
Researchers from Empa and Zurich University have been looking at the so-called corannulene molecule for answers. This molecule has five-fold symmetry and is shaped like a bowl. It is regarded as a fragment of buckminster-fullerene – popularly know as a buckyball – and for this reason corannulene molecules are also known as buckybowls. The carbon atoms in a corannulene molecule are arranged in five hexagons surrounding a central pentagonal ring.
The hope is that corannulene and its derivatives will play an important part in the development of new material systems, particularly for applications involving photovoltaics and electronics.
In order to observe how molecules with five-fold symmetry form two dimensional crystals on metallic surfaces, Empa scientists used a scanning tunnel microscope. They expected to see either an irregular structure or perfectly oriented molecules with a crystal lattice symmetry whose value was not five. In actual fact the molecules “cheated” – so as to achieve the highest possible packing density on the surface they “tilted” away from fivefold symmetry.
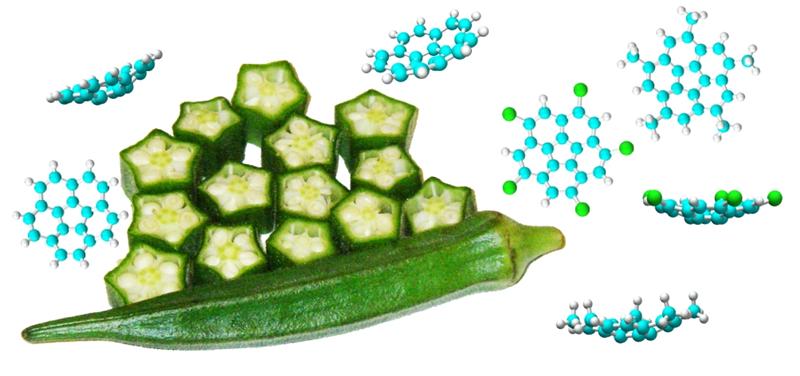
Examples from chemistry and nature: five-fold symmetry is not just found in “buckybowls”, it is also seen in the cross section of an okra pod.
An almost regular crystal lattice
In a further experiment the scientists therefore used molecules with bulky lateral groups which prevented them from tilting and forced five-fold symmetry to be maintained. Even so the molecules packed themselves tightly together. In the two dimensional crystals the molecules aligned themselves with a hexagonal lattice, that is with six-fold symmetry. But in contrast to molecules with six-fold symmetry the individual corannulene molecules differed in their orientation to each other.
This result, which the researchers recently published in the scientific publication Journal of the American Chemical Society, had been predicted both by mathematical simulations as well as by simple mechanical modeling using pentagonal polystyrene and aluminium disks on air beds and shaker tables.
The process by which the symmetry is reduced, that is the way in which the molecules achieve a regular packing structure while departing from five-fold symmetry, offers an insight into the fundamental processes of crystal formation. Monitoring these complicated processes at the molecular level using the scanning tunnel microscope is a valuable aid to understanding the different aspects of how molecules are deposited onto surfaces and how, for example, material systems can be lent new characteristics.
Article: Bauert T., Merz L., Bandera D., Parschau M., Siegel J. S. Ernst K.-H., Building 2D Crystals from 5-Fold-Symmetric Molecules. Journal of the American Chemical Society, 131 (2009) 3460-3461






Comments