Forty years ago, mathematician Mark Kac asked the theoretical question, "Can one hear the shape of a drum?"
If drums of different shapes always produce their own unique sound spectrum, then it should be possible to identify the shape of a specific drum merely by studying its spectrum, thus "hearing" the drum's shape (a procedure analogous to spectroscopy, the way scientists detect the composition of a faraway star by studying its light spectrum).
But what if two drums of different shapes could emit exactly the same sound? If so, it would be impossible to work backward from the spectrum and uniquely surmise the physical structure of the drum, because there would be more than one correct answer to the question.
It took until the 1990s for mathematicians to prove that, in fact, two drums of different shapes could produce the same sound. In other words, you can't hear the shape of a drum. That outcome, which was physically verified in one instance with vibrations on the surface of soap bubbles, raised theoretical questions about spectroscopy.
"This revolutionized our conception of the fundamental connections between shape and sound, but also had profound implications for spectroscopy in general, because it introduced an ambiguity," according to Stanford physicist Hari Manoharan.
For Manoharan, the next step in studying this conundrum was to take the drum question to another level—a much lower level. He and his students investigated the drum question in the quantum realm, where it could have an effect on real nano-electronic systems.
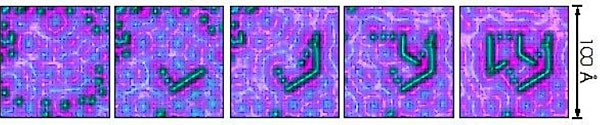
Using a tunneling scanning microscope and two roomfuls of equipment to move around individual carbon monoxide molecules on a copper surface, they built tiny walls only one-molecule high and shaped them into nine-sided enclosures that could resonate like drums (because of the quantum wave/particle duality of the electrons within the enclosure).
Manoharan calls these enclosures quantum drums. Each drum has only 30 or so electrons inside. They are walled in by roughly100 carbon monoxide molecules.
The result? Just as in the normal world, two nanostructures with different shapes can resonate in the same way, a phenomenon known as isospectrality. Manoharan, along with his graduate student Chris Moon and others, published their result in the Feb 8 edition of the journal Science. To reinforce the point, they created a video, complete with two quantum drums beating with the same sound. (The real "sound" is at ultra-high frequencies in the terahertz range; in the video, the sound has been converted to the range of human hearing.)
The practical value of having two different nanostructures with identical properties may lie in the design of ever-smaller computer chip circuits, Manoharan said. Designers of nano-electronic circuits will have two ways to get the same result. "Now your design palette is twice as big," he said.
While the chip industry attempts to shrink existing circuitry, Manoharan is literally coming from the opposite direction. "My research asks, what if you start at the bottom of the ladder? We assemble structures one atom at a time," he said. The unexplored gap between bottom-up research and the industry's shrink-down effort "is where the excitement is," he said.
The work has a natural connection to the problems of quantum computing, he said.
The research may also have connections to string theory, used by cosmologists attempting to understand the structure of the universe, Manoharan said: "There is somehow embedded into the topology of our universe this bizarre spectral ambiguity." String theories describe complex surfaces that are higher-dimensional analogues of these two-dimensional quantum drums.
The drum research has another finding important to the world of quantum mechanics. While it is impossible to directly observe the quantum phase of the wave functions of the electrons inside the drum structure, Manoharan's team has devised a way to extract that information by taking measurements from two isospectral drums and then mathematically combining the information, a process called quantum transplantation.
"We discovered that this extra degree of freedom in geometry provides us with a method to 'cheat' quantum mechanics and obtain normally obscured quantum-mechanical phase information," Manoharan said.
There are other ways to experimentally determine quantum phase information from atoms or molecules in gases, or from quantum dots and rings, all of them relying on a process called interferometry. The addition of a new method, "geometry over interferometry," will benefit researchers, Manoharan said.






Comments