The all electron
full-potential linearized augmented plane wave plus local orbitals method was
utilized to study the structural properties of ZnO (0001) ultra-thin films
(nanosheets). From the calculations, it was observed that in the presence of
oxygen vacancies at the Zn-terminated (0001) surface of the ZnO nanosheets, the
structural phase transformation from the graphite-like structure to wurtzite
lattice occur even if the thickness of the ZnO nanosheet along the c-axis is
less than or equal to 4 atomic graphite-like layers [J. Appl. Phys. 113, 014304 (2013)].
Most of the
synthesized Zinc oxide (ZnO) nanostructures in different geometric
configurations such as nanowires, nanorods, nanobelts and nanosheets
(ultra-thin films) are usually in the wurtzite crystal structure. Cutting of
the ZnO (0001) thin film perpendicular to the [0001] axis always result in a
Zn-terminated (0001) surface and O-terminated (000-1) surface. For these Tasker type III polar surfaces [1],
there are several stabilization mechanisms for the reduction of the divergence
of surface energy such as the charge transfer from the anion surface to the
cation surface [2]. However, it was found from density functional theory
calculations that for ultra-thin films of ZnO, the graphite-like structure was
energetically more favourable as compared to the wurtzite structure [3]. The
stability of this phase transformation of wurtzite lattice to graphite-like
structure of the ZnO nanosheets is only limited to the thickness of about few
Zn-O layers (along the c-axis), beyond which they revert back to the wurtzite
phase, and this was subsequently verified by ZnO nanosheets grown by pulsed
laser deposition [4].
Conversely, the transition from wurtzite to a
graphite-like phase is also observed for ZnO nanostructures under tensile
strain [5]. Due to the special properties of graphene, these graphite-like ZnO
nanosheets have attracted much interest but the influence of oxygen vacancies
on the important transition when the ZnO nanosheets revert back from the
graphite-like phase to the wurtzite structure had been scarcely reported [6].
Hence in this short note, we would like to highlight this important result that
was reported in Ref. [6] (obtained using first-principle calculations), which
will provide useful guidelines for future experimental explorations.
The calculations on the ZnO nanosheets
are carried out using the density functional theory method implemented in the
Wien2k code [7] and utilizing the revised Perdew-Burke-Ernzerholf (PBE)sol
generalized gradient approximation (GGA) parametrization scheme as this
functional is known to provide good results for solids and their surfaces as
compared to hybrid DFT functional which are 2 to 3 orders more expansive
computationally [8]. The ZnO (0001) nanosheets are modelled by supercell slab
(SS) by stacking the bulk unit cell of wurtzite ZnO in the c-axis of hexagonal lattice,
with the Zn (O) atom layer terminating at the basal plane along the [0001] ([000-1]) directions.
In addition, there is a vacuum layer of
several angstroms to eliminate the neighboring interactions between the periodic SS.
The convergence of the optimized SSs are ensured by selecting the appropriate
Monkhorst-Pack [9] k-point mesh and are found to be sufficient to achieve a
self-consistent minimum total energy below 0.1 mRy. For further computational
details, please refer to Ref. [6].
The transition from the bulk-like
wurtzite structure to the graphite-like structure for the nanosheets of
different sizes is due to a number of different factors. One of the important
factors is due to the competition between the bonding energy and the
electrostatic energy that finally triggers a structural phase transformation
from wurtzite structure to graphite-like structure when the thickness of the nanosheet
is lesser than a certain number of Zn – O layers along the [0001] direction [6].
The extreme surface Zn and O atoms of the smaller nanosheets have already lost
one of the four bonds due to the surface termination as compared to bulk ZnO, a
larger surface to volume ratio for these smaller nanosheets ensures that they
are unable to compensate for these broken surface bonds together with the
stronger Coulomb’s attraction from the interior atomic layers.
This then
triggers a collapse of surface atomic layers towards the interior of the
nanosheets and thus results in flattening of the atomic layers and hence a
phase transformation from the wurtzite lattice to graphite-like lattice for the
thinner ZnO nanosheets [6]. In addition, the nature of the bond and energy due to
the macroscopic electric field in the [0001] direction are also contributory
factors to the phase transformation. Importantly, the creation of surface
O-vacancy at the Zn-terminated (0001) surface of the ZnO (0001) nanosheets as
depicted in Fig. 4 of Ref. [6] results in the removal of the stronger Coulomb’s
attraction at the Zn-terminated (0001) surface.
Furthermore, (after the
introduction of oxygen vacancies at the Zn-terminated (0001) surface of the ZnO
(0001) nanosheets,) the reverting of the
structural phase transformation from the graphite-like structure back to the wurtzite
lattice occur even if the thickness of the ZnO nanosheet along the c-axis is
less than or equal to 4 atomic graphite-like layers. This can be observed in
Fig. 4(a) (top panel corresponding to the perfect ZnO nanosheets) as compared
to the defective ZnO nanosheet [bottom panel of Fig. 4(a)] in Ref. [6]. Alternatively, the phase transformation of the defective ZnO nanosheet could also be observed in the figure below. 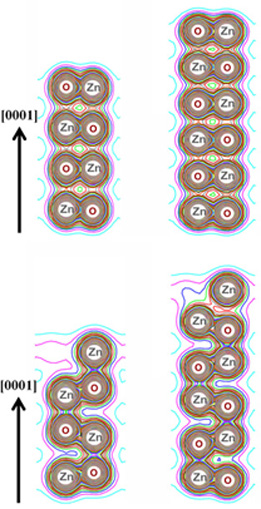
Top panel – Perfect ZnO nanosheet in the graphite-like structure and Bottom panel – Phase Transformation of the defective ZnO nanosheet from the graphite-like structure to the wurtzite structure with oxygen vacancies at the Zn-terminated (0001) surface
Therefore
the presence of oxygen vacancies results in eliminating the size-dependent
graphite-like structural phase transformation for the defective ZnO nanosheets
[6].
For further details on the effect of the
oxygen vacancies on the defect formation energy, charge density and electronic
band structure of the ZnO (0001) nanosheets of different sizes at the
Zn-terminated and O-terminated surfaces, the reader is referred to pages 6-8 in
Ref. [6] One important effect on the creation of the oxygen vacancies is
enhancement of the surface metallization of the defective ZnO nanosheets [6].
The graphitic ZnO thin films are structurally similar to the multilayer of
graphite and are expected to have interesting mechanical and electronic
properties for potential nanoscale applications.
References
[1] P. W. Tasker, J. Phys. C: Solid State 12, 4977 (1979).
[2] A. Wander, F. Schedin, P. Steadman, A. Norris, R. McGrath, T. S. Turner, G. Thornton, and N. M. Harrison, Phys. Rev. Lett. 86, 3811 (2001).
[3] Z. C. Tu, and X. Hu, Phys. Rev. B, 74, 035434 (2006).
[4] C. Tusche, H. L. Meyerheim, and J. Kirschner, Phys. Rev. Lett., 99, 026102 (2007).
[5] A. J. Kulkarni, M. Zhou, K. Sarasamak, and S. Limpijumnong, Phys. Rev. Lett., 97, 105502 (2006).
[6] K. M. Wong, S. M. Alay-e-Abbas, A. Shaukat, Y. Fang, and Y. Lei, J. Appl. Phys., 113, 014304 (2013). This is an open access article which can be freely downloadable at:
http://jap.aip.org/resource/1/japiau/v113/i1/p014304_s1?bypassSSO=1
[7] P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, and J. Luitz, WIEN2K, an Augmented Plane Wave p Local Orbitals Program for Calculating Crystal Properties (Karlheinz Schwarz, Techn. Universit€at Wien, Austria, 2001).
[8] J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou, and K. Burke, Phys. Rev. Lett. 100, 136406 (2008).
[9] H. J. Monkhorst and J. D. Pack, Phys. Rev. B 13, 5188 (1976).





Comments