The topic of today is in fact potentially explosive - how experiments perform their blind searches and the potential bias that results from the detailed procedures they employ. However, you will be disappointed by reading this article if you search for scandal and flame: I am going to explain why CMS does excellent science.
The starting point is Philip Gibbs blog entry of yesterday, which in turn is triggered by the release of a video by the CMS collaboration, where small clips of internal meetings are shown. The meetings in question are ones held in mid June last year, when the collaboration was seeing for the first time the results of Higgs boson searches in the most sensitive low-mass channel, the decay to photon pairs which eventually was the backbone of the discovery claim that both ATLAS and CMS were able to put forth on July 4th.
Philip argues that the procedure of unblinding the data and then doing a top-up of a part of the statistics is not exactly one which makes the results totally unbiased. Although I believe Phil cannot infer the full story about the real procedures in CMS from the voluntarily short and fragmented video, he is at least in principle correct on the issue of the bias. However, in his post he prefers to not explain (I am sure he knows, because he is a quite smart guy) that bias is not the full story in a measurement.
I would be tempted to make a digression here, discussing the tradeoff between bias and variance in specific statistical procedures (e.g. unfolding), but I will save your and my time today, and get to the heart of the matter.
Let me also leave totally aside the issue of how a bias could arise, in principle, from the exact procedure used by CMS in the case at hand, and discuss instead a generalized procedure that is common to many particle physics experiments nowadays when they perform blind analyses. This will allow us to focus on the important points without being distracted by accidental details.
How a bias may arise from your procedure
You perform a measurement, obtaining your final result by doing some statistical analysis on the data. This analysis is complex, so there are dozens of assumptions, estimates of ancillary quantities that enter the calculation, etcetera. In the course of your analysis you might have done mistakes of all kinds. You were careful to cross-check each ingredient, of course, and only upon being convinced that you did everything well do you proceed to "turn the crank" and produce the actual result. This is what we call a "blind analysis" in HEP: it is blind in the sense that you take some precautions to avoid biasing yourself into taking decisions on the method you apply based on the knowledge of what effect those decisions might have on the result -its moving away from the range of values you subjectively consider most likely for the physical quantity you are measuring, for instance. In other words, you do not know what the result will be until you obtain it.
When you "open the box" and stare at the result, most of the times that will be the end of the story as far as you, as analyst, are concerned: you are ready to present it as a preliminary result. Indeed, a blind analysis should be published as is upon unblinding, in order to avoid the biasing effect you wanted to remove in the first place, right ?
Well, in principle that is correct: if, upon observing that your result is way off what you consider the "right" answer, you were to delay publication and go back to a complete re-check of the whole analysis chain, with the potential of finding new improvements and changing things here and there, the philosophy of the blind analysis would be spoiled, at least in part. In an ensemble of physics results performed with such a technique, those results falling off the previously known value of the measured quantity would be depleted. This is what is called a selection bias.
Why it is not such a bad thing
What experimenters do, however, is not to dread bias as a completely evil thing. Sometimes, one accepts bias in order to reduce the variance of the measurement. Statisticians explain that the mean square error - the expectation value of the square of the difference between the observed value and the true value of a quantity you are measuring - is the sum of two terms: squared bias, and variance. Variance is determined by the precision of your measurement; bias is connected to the accuracy, as is well explained by the graph on the right, courtesy wikipedia.MSE = b^2 + σ^2
where b is bias and σ^2 is the variance. Note that what we really want from our measurement is to make as small as we can is the mean square error, not individually b or σ! Now, imagine that our procedure of re-checking "weird" results produces a bias b. If, however, the re-checking of those weird results (which, crucially, are the ones which are the most likely to be affected by a mistake, and thus are most likely to have a large variance σ!) you are able to reduce their variance -by correcting any mistake you may find out you have made-, then you may end up winning: you accept some bias but reduce the variance, and the MSE may be smaller.
Testing the claim: a prototypical experiment
In order to convince you that this is not just a theoretical wishful thinking but the reality of things, let us imagine that we are measuring a quantity which we believe to be zero with an instrument whose precision is 1. Sometimes, however -say 3% of the times- we make a mistake, and we add a contribution to the total error which is five times as large. So the "normal" variance for the cases when we do not commit a mistake is 1, and the "screwed-up" variance is 25+1=26. This may appear as an extreme situation, but our conclusions will not depend much on the magnitude of the chosen numbers.
Now, what we do is to study the two possible behaviours: A) we accept the result regardless of the value we get; B) we scrutinize more carefully those results which are more than two standard deviations away from our "preferred" value of x=0. Here "standard deviation" means the error we think we are making (σ=1), not the one we may sometimes be making (σ=sqrt(26)).
In B), we suppose we always end up correcting for the mistake, but our intervention results in modifying the measurement, such that we re-determine x (with σ=1).
This procedure can be tested with pseudoexperiments. What I show below is, as a value of the true x ranging from -10 to +10, the mean square error (i.e. the average of the square of the deviation between our final measurement and the true value of x) we may expect depending on our chosen measurement strategy, A (in black) or B (in red).
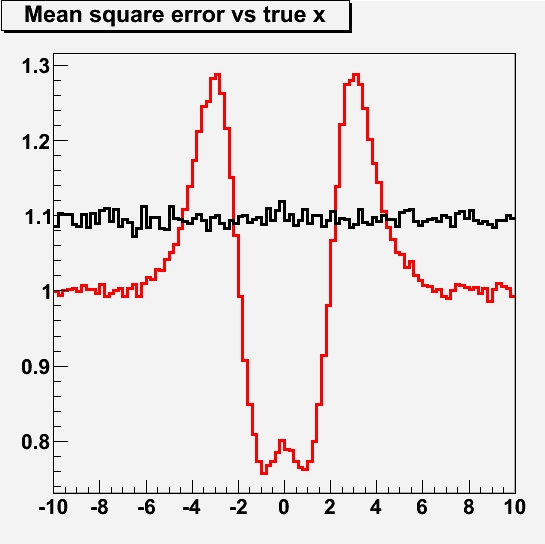
As you can see, the MSE for case A lies mostly a bit above 1: that is because our standard error (which is indeed 1) gets "polluted" with the small percentage of cases when there was an additional large source of uncertainty. Also, you observe no dependence of the true MSE on the true value of the quantity being measured: the distribution is flat, as it should be -you take no action depending on the returned value of your measurement, and the experiment is truly "blind".
In case B we have a more interesting behaviour: you first of all observe that asymptotically -when the true value is large, that is at the very left and very right of the graph- it pays to have corrected our mistakes: by finding a large measured x, we have reduced the error to what our measurement device provides in the absence of further smearing, i.e. σ=1.
Then, you also see that for true values of x close to zero, your idea of re-checking results which are far from zero also pays off: you are then likely to spot the measurements affected by the extra uncertainty, and removing it allows you to reduce the total MSE. Note that, by virtue of doing this for the cases when x is large, your total MSE ends up being smaller than 1! That is due to your accepting small results when the true x is small.
The most interesting feature of the red curve is however the spikes at +-3. These are due to the procedure as well: when x=3, for instance, there is a significant chance that you get a measured value close to 3, in the absence of additional mistakes in your measurement. Such a value is flagged by procedure B) as faulty, and you end up scrutinizing it more carefully, eventually finding nothing but in the meantime changing things here and there, and ending up with a different measurement, which has a sizable chance to be farther from the true value than it used to be: that is the cause of the increased mean square error!
I find this example instructive, and actually I myself learned something from carrying it out (writing the macro that produced that graph took me a small fraction of the time of writing this article!). What is the message to carry home ? I think the message is: don't be obsessed with bias alone, and always consider what the mean-square-error of your measurement procedure is. However, if you insist that the coverage properties of your measurement are fully independent on the true value of the quantity being measured, then you should consider a truly blind approach, i.e. one which reports whatever value you get regardless of your prior beliefs on the likely values of the physical constant you are determining.
Note also that the pseudoexperiments above describe a very unfortunate case for the experimenter: we have given much more weight to x being different from zero than to x being compatible with zero! In reality, we have reasons to assign a larger weight to our theory being correct (x=0 in this case), so if we are Bayesians we may like the kind of approach provided by procedure B)!
Comments