In a paper appeared a few days ago on the Cornell Arxiv Campbell, Ellis and Williams discuss how the LHC experiments have a chance to obtain information on the Higgs boson width by studying four-lepton events at masses much above the 126 GeV region where they cluster when produced by Higgs boson decays. Here I am going to show the graph that is at the source of this idea, and the general conclusions that the theorists reach on the precision that ATLAS and CMS can obtain on that parameter.

First of all let me explain to outsiders what is the Higgs boson width. In order to do so I need to make a short digression.

Elementary particles are characterized by several parameters that define their behaviour. Some of these, like the spin, are the same for every one we produce: the Higgs spin is zero, and it is identically so for all Higgs particles we observe. Mass, on the other hand, is different for each one of them. This is due to their very short lifetime: like a low-pitch string kept vibrating for a time so short that we cannot determine the exact pitch, a short-lifetime particle has an associated uncertainty in the mass. If we had an infinite-precision measuring device, and we histogrammed the observed mass of a large number of Higgs bosons, we would find that this is a characteristic "resonance" shape, a Breit-Wigner (aka Lorenzian) shape: a peaked structure, with peak equal to the nominal particle mass, with long tails extending indefinitely.

Because of the Lorenzian shape of the resonance, we can sometimes observe particles with a mass quite different from their nominal value. In some cases, the study of the resulting distribution of masses allows us to directly measure the intrinsic width of the resonance curve: this is another fundamental parameter of the particle, and one capable of discriminating its nature. For the Higgs, a precise measurement of the width would allow us to distinguish different new physics models. New physics alters the width because the possibility of the Higgs to decay to some hypothetical new particle would provide extra chances of decay, thus making the lifetime shorter and the width consequently larger (lifetime and width are inversely proportional).

The problem with the Higgs boson is that its lifetime, while fantastically short in absolute terms, is rather long with respect to those of other particles of similar mass: the top quark, for instance, is 40% heavier and has a much shorter lifetime, and a consequently much larger width (1.5 GeV); the Z boson, which is instead 30% leaner, has a 2.5 GeV width (and is thus the shortest-lifetime particle we know). The Higgs boson has a width of just 4 MeV or so. Measuring such a small width is impossible by direct means, because the experimental uncertainty on the observable invariant mass of e.g. two photons produced in Higgs decay, or four charged leptons from the H->ZZ->4l decay chain, is three order of magnitude larger. It is like you tried to determine the weight of an ant using your body weight scale as a measuring instrument.

But there are workarounds. The quantum world is quite a bit more complicated than we can usually describe in simple terms, and in fact when I told you above that the mass distribution of Higgs bosons is a Lorenzian I, stricly speaking, lied. Theorists in fact computed interference effects and other complex mechanisms, and they came up with a shape which is quite more featureful than a simple resonance shape, as you can see below.


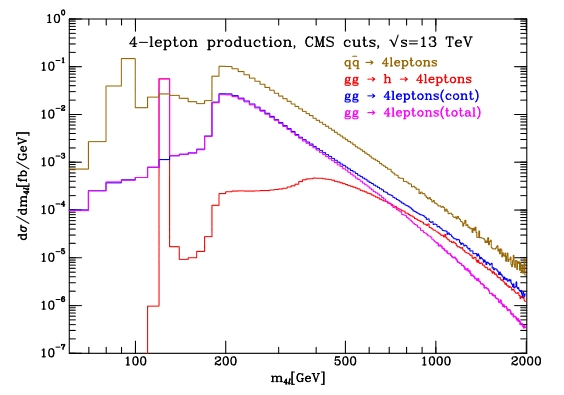
The Higgs-induced four-lepton mass distribution is in red, and is compared to the main backgrounds (in blue, brown, and purple). As you can see the peaking structure at 126 GeV is accompanied by a funny tail at high mass, which takes its shape from the "opening" of the decay to pairs of real Z bosons (at 182 GeV) and to the increase in cross section of virtual Higgs bosons by the intervention of initial states involving pairs of real top quarks (at 350 GeV).

The hope that a measurement of some detectable features of the complicated red shape in the graph above can produce a direct inference on the value of the Higgs boson width is reasonable. With the 2015 run the LHC will provide to ATLAS and CMS collisions at 13 and then 14 TeV, and a much larger integrated luminosity. This will mean more Higgs events, and hopefully some tight upper limits on the Higgs width, which will tell us more about the true nature of the goddamn particle. But already with the data collected this far the exercise is possible; the result is that the width cannot be larger than a few tens of times what the Standard Model predicts. Not very informative, but still a beginning in this difficult field of investigation.

UPDATE: I was asked to mention that the first paper discussing the funny shape of the distribution, and its implications, belong to a paper by G.Passarino and N.Kauer.