But why bother ? Well, of course because there is a real challenge on: bookmakers need to tune the odds they offer!
Fermilab versus CERN
The hunt for the Higgs boson has been a hot topic in high-energy particle physics for decades now, but the excitement has arguably never been higher. The reason is that to the burning importance of the issue of the existence of the Higgs boson, the gasoline of a new chapter in the decades-long rivalry between America and Europe in particle physics is being thrown in. The stake is high!
In the past the Fermilab versus CERN challenge was largely an indirect one: after the early seventies, when neutral currents were sought with similar means on both sides of the Atlantic, the two laboratories started to pursue different goals, with different means. This differentiation has its roots in the increase of size, and budget, of the experimental facilities required to dig deeper and deeper in the structure of matter: particle physics turned global, and it suddenly became evident that it was illogical to duplicate efforts, at least the biggest ones.
At the recent Chamonix workshop CERN decided that the LHC will run without shutdowns for the next two years at the reduced center-of-mass energy of 7 TeV, collecting a foreseen total of one inverse femtobarn of proton-proton collisions. In the light of that, the overlap in discovery or exclusion prospects for the Higgs boson of the Tevatron and LHC experiments is quite large. It will be a fierce competition!
Learning from the past
So the above explains why it is not a vacuous exercise to try and gauge the future potential of CDF and DZERO in the hunt for the Higgs boson. What I have done in the past, and I will offer in a updated version today, is a comparison between the 1999 predictions and the most recent results on the ratio between observed and standard-model-predicted cross section of Higgs production. Let me explain better.
Once a mass for the Higgs boson is hypothesized, the standard model can be used to predict how many Higgs events, N, we should see in a given amount of data. If then the experiments manage to exclude that the data contains M or more events, one can say that Higgs production has certainly a rate that is less than R=M/N times the standard model predicted rate. If R is less than 1, the corresponding mass hypothesis has to be rejected.
11 years ago, before any data were collected by the CDF and DZERO experiments in Run II, the SUSY-Higgs 1999 Tevatron working group produced the graph shown below.
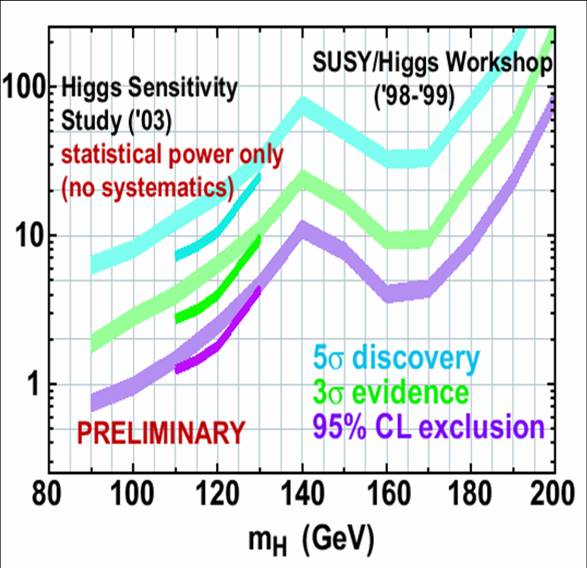
Let us consider only the purple band: it shows, as a function of higgs mass, the amount of data (in inverse femtobarns, on the vertical axis) that, if collected by CDF and DZERO, could be predicted to yield an exclusion of the corresponding mass (on the horizontal axis), at 95% confidence level: id est, a limit R<1. We can take that luminosity and compare it to the luminosity used by CDF to obtain their latest Higgs limits combination -that of November 2009, which is shown below.
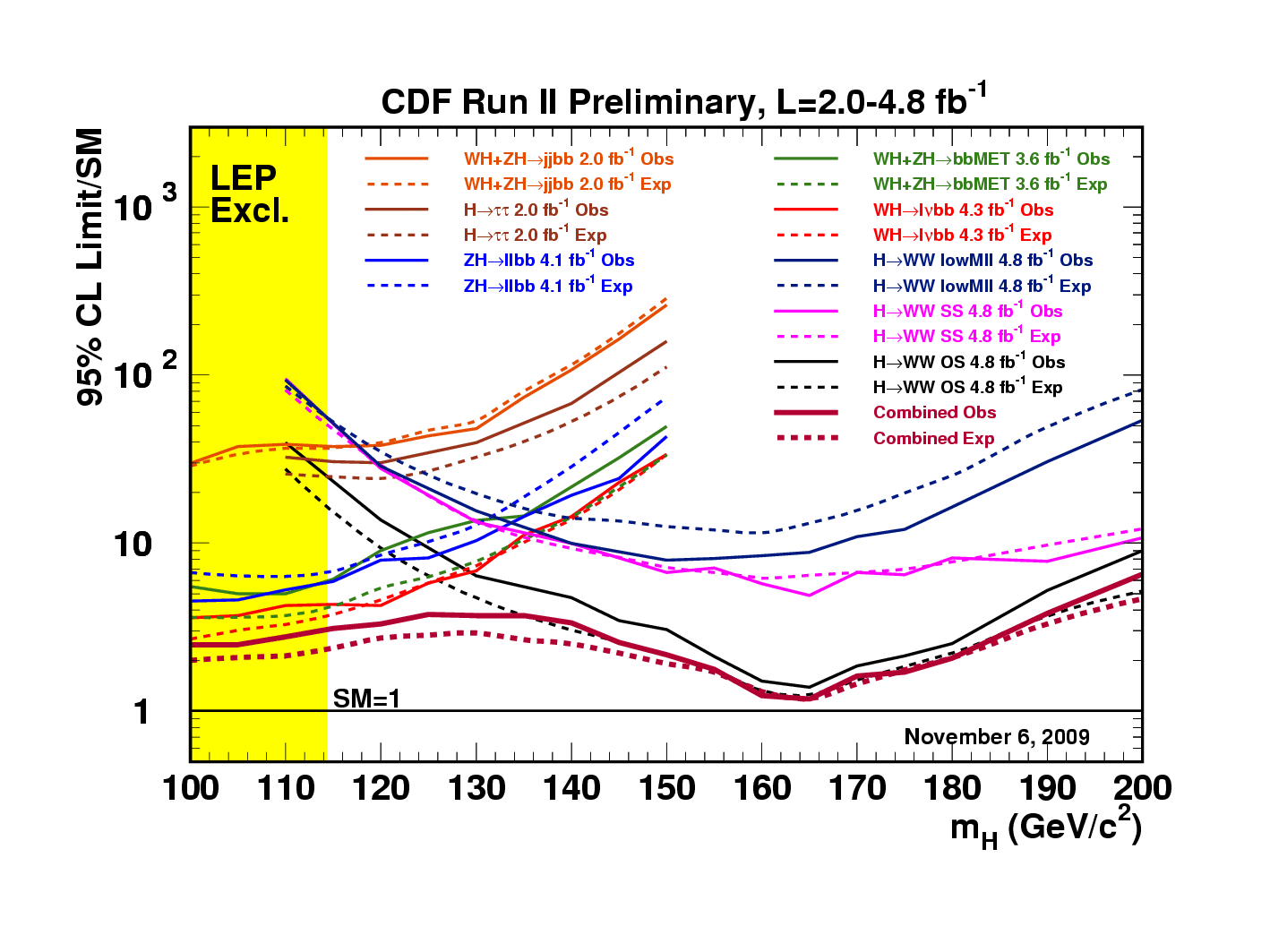
In this very crowded graph you see the R limits as a function of Higgs mass, obtained by each of several different analyses. Their combination is the lowest-lying, thick red curve. At low mass, the game is dominated by searches involving the associated production of Higgs and vector boson -WH and ZH, in red and blue- and the decay of the Higgs to pairs of b-quarks. At high mass, the Higgs most readily decays into pairs of W bosons, and so the corresponding search (whose limit line is in black) is the one which drives the combined limit.
How to relate the 1999 predictions -which tell of a luminosity to reach R=1- with the CDF 2009 results -which tell the R limit with a given luminosity ? It is not that difficult, but it entails a couple of assumptions and a few square roots.
First, we assume that CDF+DZERO = 2 x CDF, that is that the two experiments have similar sensitivities: we need to do that if we want to take as a basis the above CDF results; besides, the 1999 predictions also used a "standardized Tevatron detector" as a basis, trying to average the capabilities of the design of the two experiments. Then, we assume that limits scale with the square root of the available data -a well-tested fact that basically rests on the known Poisson behavior of the uncertainty in the number of events that the experiments observe when they search for a particle.
From those two assumptions it follows that if we see a ratio R=2 limited by CDF, we must assume that, once the same size of data from DZERO is added, a combined limit of R'=2/(sqrt(2))= 1.4 can be obtained. That is step zero in our conversion from 1999 to 2009.
Then we need to obtain a "weighted average" of the luminosity actually employed by CDF at each mass value to obtain the limit shown in the figure above. That is because different analyses employed different amounts of data to obtain the limits shown. We must weight the luminosity by the inverse of the squares of the R ratio limits that the different analyses expected to place -the "strength" of the different searches, that is. Why the square ? Because the sensitivity on R goes with the square root of the luminosity, as noted above.
Once for each mass value we have the equivalent luminosity L_eq, we can determine the R limit that CDF was expected to obtain with it as R'=sqrt(2*L(R=1)/L_eq). This amounts to saying: if with luminosity L(R=1) in 1999 they expected to obtain R=1, that means they foresaw a limit R' with luminosity L_eq. The square root, again, takes care of the connection between R reach and data size. The factor of 2 instead takes care of considering that CDF is only one experiment, so R' is sqrt(2) times larger.
Fine, so now we have a set of R' values, one per each Higgs mass: they represent the prediction of 1999. We may compare them with the R-values actually excluded by CDF in November 1999. To do so, we further take the ratio of the latter divided by the former, to obtain a number which says how much worse CDF is doing with respect to 1999 predictions! Values larger than 1 mean that the predictions were overoptimistic; values around 1 mean that they were right on the money. This is shown below.
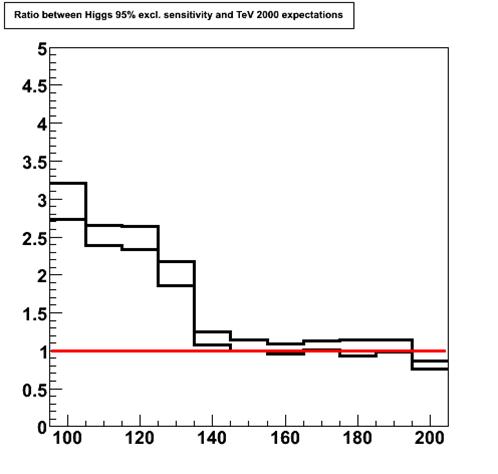
The black histograms "frame" the ratio between actual 2009 sensitivity and 1999 predictions, while the red line highlights where the ratio is one. It clearly looks like the predictions were 2.5 times overoptimistic for low Higgs mass values, and perfect for masses above 135 GeV. This is both surprising and not surprising.
It is not surprising to see that the 1999 predictions for the reach at low mass were overestimated! In fact, they were computed by taking in account the potentiality of a silicon detector upgrade that was not funded. And the silicon detector is the critical component for the detection of the b-quark jets into which a low-mass Higgs boson decays: less silicon, lower efficiency for low-mass Higgs decays, and worse reach in the Higgs search. A small part of the overestimate is also due to optimism in my humble opinion (I was one of the authors of the 1999 study, and I am well-known for my optimism despite my bleak predictions for SUSY discoveries at the LHC...).
It is instead surprising, at least to me, to see how closely the high-mass sensitivity was foreseen to be in 1999! It looks like an act of divination. Please recall that for the 1999 study we could use the already analyzed Tevatron Run I data and the acquired knowledge on the tools that were at hand at the time, but we could only make educated guesses on the tools that were not yet developed to increase the purity of leptons selection, background separation, increase the trigger efficiency, etcetera, etcetera, etcetera. And those guesses now appear to have been really, really well-educated!
The future from the past
So we learn the following lesson: the high-mass reach extrapolations of 1999 are quite trustable. The low-mass reach was harder to estimate back then, especially since we were basing our extrapolations on a detector that would never be funded to build. And now let us turn to the present extrapolations, again produced by CDF.
The plot below shows the exclusion in R that CDF could achieve, for a Higgs boson mass of 115 GeV, as a function of the integrated luminosity employed by the analyses. Besides noting the incredible progress that has been achieved from the early analyses to the more refined recent ones -a downward trend that signifies an increase in effective luminosity by a factor of 5-, one sees that the 115 GeV Higgs boson might be excluded by CDF with a luminosity of the order of 15-20 inverse femtobarns (the graph stops at 14/fb, but you can sort of eyeball these numbers anyway, by guessing where the light-brown band goes below the line at R=1). Or by CDF and DZERO with 7.5-10 inverse femtobarns each.
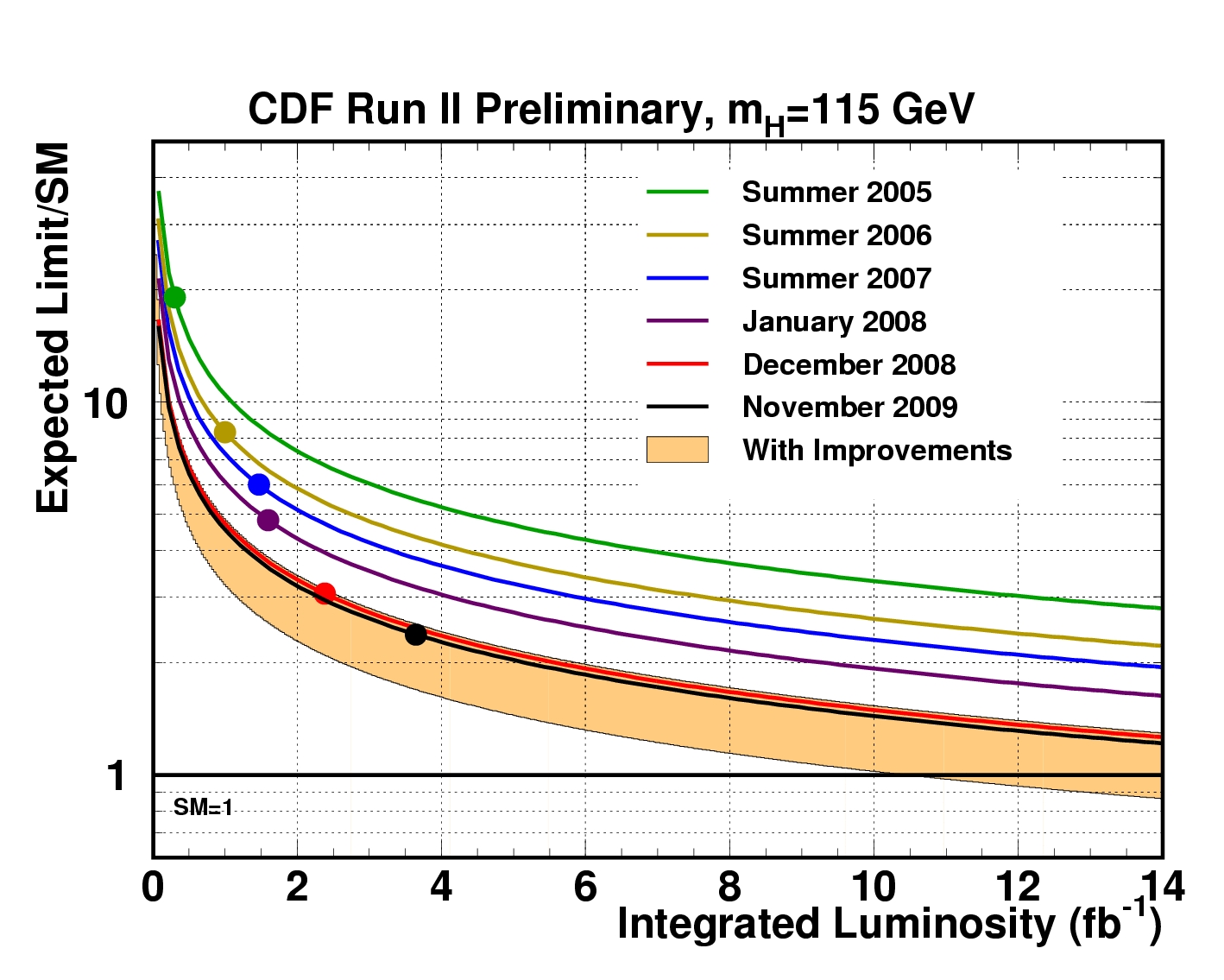
Now, with the help of the first figure above (the 1999 predictions), we see that 10 inverse femtobarns collected by the two Tevatron experiments might be enough to exclude a Higgs mass range all the way from 115 GeV (the LEP II limit, below which no standard model Higgs boson can be thought to exist) to 180 GeV: the high-mass reach is trustworthy, as noted above. And 10 inverse femtobarns per experiment are a quite credible possibility for CDF and DZERO to have bagged by the time 2011 ends!
As you will have noticed by now, I am only talking about excluding the Higgs boson, and not discovering a signal. I believe that the Higgs boson is light: probably in the 115 to 130 GeV range. In this range neither the Tevatron nor the LHC experiments will have a sizable chance of seeing a clear signal. However, if a 120 GeV Higgs were there, the Tevatron limits at 120 GeV could be insufficient to rule it out there -somehow diminishing the achievable result!
Conclusions
The LHC experiments will be unable, in my opinion, to make up in two years of data taking, and with the 3.5 times larger energy, for the 8-year advantage in running time of the Tevatron. The Higgs boson will be unlikely to be discovered before 2013, and it will probably be a sole LHC business; however, until then the Tevatron will retain the better results as far as the mass exclusion range is concerned.
A couple of links
John Conway, who incidentally was the head of the Higgs 1999 prediction effort, wrote about the outcome of the Chamonix workshop at Cosmic variance; Resonaances has a recent post where he discusses integrated luminosity in the same context; Peter Woit also discusses the outcome of Chamonix. Matthew Chalmers has a nice plain-English overview here.
A due disclaimer at the end of a rather speculative article: Beware -the above extrapolations are my own cooking, and the views expressed in this post do not reflect in any way those of the experiments and the laboratories involved.




Comments