Baseball, more so than any other sport, lends itself to numerical analysis because virtually everything except defense is rigorously quantifiable. There are some details, such as an umpire who might call a wider strike zone than another, but at least from a rules perspective the strike zone is what it is.
Numerical models have long been used to analyze the past and therefore make educated predictions about the future performance of players - a player can be expected to decline in his 30s, and certainly in his 40s, but there is no hard rule on that progression and team predictions are another issue entirely; the ability of objective math to beat out experts remains a topic of some debate. It's steel drivin' man John Henry versus the steam drill, except the modern technology is a computer.
Johnny Cash does John Henry.
Knowing that, I have no problem jumping into the debate. First, let's lay out the intellectual battlefield.
The Giants have 'home field' advantage and, if such a thing exists, it is a substantial matter - but first let's explain some terms, like 'pull' hitting and 'opposite field' hitting. A right-handed pull hitter means he will be inclined to hit the ball to his left, which is left field. An opposite field hitter means a right-handed batter hits the ball to right field. I know that isn't intuitive because a right handed guy hitting to right field doesn't sound like it would be opposite but it just is. Pull hitting generally means more home runs.
AT&T Park measures 339 feet down the left-field line and 309 down the right but it has 25-foot-tall brick wall and a breeze blowing in off McCovey Cove against left-handed pull hitters. Right-handed hitters have a 382-foot power alley in left-center field but left-handed hitters have a harder time pulling the ball out to right. The deepest part of the park is in right-center field -- 421 foot from home plate under an 18 foot high wall. Barry Bonds is the only left-handed power hitter with a meaningful number of home runs in right field in the park's short history(1).
That's a pitcher's park, folks.
Why do I say 'if such a thing exists' then? Since players are in their home field for 81 games per year, a poor hitter's park also impacts the home team's hitting - a great offensive player who can earn the same money in a park where his skill is more obvious (for example, he gets more home runs) will not go to a team with a great hitter's park, usually leaving such a team to either overpay a great hitter or sign players who have no other choices because they are not that good. That means the home field advantage evens out and statistics bear with me on that, even though the home team has won 58% of the World Series. Why? Teams that won the first game but lost the second only won 45% of World Series but teams that lost the first and won the second brought the trophy home 71% of the time. The home field advantage, if it exists, is psychological and not actually a park effect.
But psychology matters too, and the Giants have a strong pitching roster, having defeated the Braves (predicted in Science Of Baseball Playoffs: Giants To Win LDS, But Don't Bet The House) and, more surprisingly, the Phillies, which has been a confidence boost.
But despite having terrific pitching in a pitcher's park and having beaten a team with superior hitting, fielding and baserunning, the math still says the Texas Rangers have a 65.1% chance of winning the World Series. How can that be?
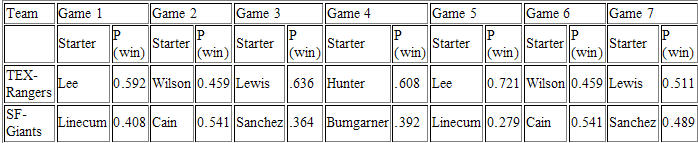
It's because some stats have meaning and some do not. A meaningless statistic is, for example, that the Rangers have lost 7 consecutive games to the Giants in interleague play. A meaningful statistic is that Josh Hamilton has channeled Lou Gehrig of the 'Murderer's Row' New Yankees and hit .359 with 30 home runs and 100 RBIs. No one on the Giants even has 90 RBIs which means they are a rather anemic offense by comparison.
But perhaps our good friend Thomas Bayes can make sense of the chaos of statistics, or at least make mathematical probability out of epistemological uncertainty. First, a few words on Bayes because, like 'opposite field' hitting meaning the same field as hand you bat with, it is counter-intuitive.
Bayes theorem is the conditional probability of a Hypothesis (H), its probability after Evidence (E) is observed in terms of the prior probability of H, the prior probability of E, and the conditional probability of E given H. That's a little messy but it basically means the probability of an event like a homerun (HR) given an event FB (a fastball pitched) depends not only on the relationship between events HR and FB (such as how often the player hits fastballs for homeruns) but on the marginal probability (or "simple probability") of occurrence of fastballs and homeruns.
Using Bayes rules, our favorite baseball mathematician, New Jersey Institute of Technology associate math professor Bruce Bukiet, says that the Rangers are going to win 65.1% of the time but probability is an index of subjective confidence.
So bet on the Rangers, right? Well, no, that is not how it works because there are two teams and each can only win or lose. Like flipping a coin, 50 times out of 100 you would expect heads but how much would you bet that on 7 flips it would be heads 4 times if the percentage of that occurring was 65.1%? Thus, you see how Bayes can often be misused (read: by sociologists) and misunderstood (read: by most everyone) when it suits them. It takes "Lies, damn lies and statistics" to a whole different level.
In reality, the Giants don't need to win 34.9 games out of 100, they only need to win 4 - tossing heads 4 times out of 7 is not all that uncommon and four times in a row is less common but almost everyone has done it. So where does that leave us?
Bukiet was quite accurate overall this season, getting 6 out of 8 playoff teams correct - but that is using thousands of games over a 162 game season. On the details, like the National League West, he was completely wrong, predicting the Dodgers to win the division (they ended with a losing record instead) and the Giants to finish fourth and the Padres to finish last. In reality, those two teams were in contention until the final day of the season.
What changed? Circumstances, in the form of E based on the prior probability of H. The April roster used for predictions was a snapshot in time and some teams had acquisitions that were better than expectations and some teams had players who did far worse than predictions. And the math was not the only thing incorrect; among the experts at Sports Illustrated who presumably used no math but a lot of experience, only one picked the Giants to win their division and the other columnists were probably making goat noises at Ted Keith for doing so.
In the post-season, statistical anomalies occur more for hitters than for pitchers because the defense has the ball, so it is one batter against 9 fielders - thus, someone who bats .300 for a season of 500 plus At Bats may have a run of 20 bad At Bats and do nothing but a pitcher, even with a poor night, still has other players to help. That means that in a 7-game series pitching should make the difference. Am I bucking the odds and predicting a World Series win for the Giants despite a comparatively poor offense compared to their opponents? As I mentioned in the home field advantage section, psychology is a large part of sports. Another light-hitting team, the 1988 Dodgers, went up against an offensive juggernaut in the Oakland Athletics in the World Series and one crippled player came off the bench and changed the mentality of everyone there:
The Phillies should be in the World Series, according to the math, but that is why they have to play the games. Go Giants!
NOTES:
(1). Though Aubrey Huff hit 12 of his 26 homeruns at his home park, which would not exactly make Barry Bonds feel like Wally Pipp, had they played together, but puts him at number two all-time as a left-handed hitter.




Comments