Snarky puzzle
Figure out how to represent any quaternion using 3D rotations and one complex number.
Background
Complex numbers are critical in quantum mechanics. Quaternions are the union of three complex numbers that share the same real. I find it fun to play with different interpretations of quaternions. And that is all it is at this point, play.
Answer
Start with a randomly chosen quaternion:
That has a norm of:
Pick a different quaternion that has 2 properties. First it is complex number and second it has a norm equal to the quaternion:
and
The complex number z points along the x axis. I really should do this in far more general coordinates, a fine point for a technical paper, but unnecessarily complex for a little blog post. The last step is to rotate z to point in the direction of q, to find a U such that:
where ||U|| = 1
This is the one trick wonder quaternions are known for, doing rotations in 3D space.
Discussion
The quaternions that do the rotations happen to be elements of SU(2), the unit quaternions. I make no claims about that observation, I will just file it away.
Dec 13, Spinning the Interaction Story: Spin 2 (2 of 3)
Snarky puzzle
Draw pictures of spin 0, spin 1 and spin 2. If you get stuck, think about a drain for spin 1 and a water balloon for spin 2. Spin 0 is the source for all.
Background
This question arose from simple figures in "Feynman Lectures on Gravitation." I like to quote the man:
The polarizations of a graviton is a tensor quantity. We may visualize this with pictures similar to those we use in describing stresses; we draw arrows indicating the direction to be associated with surfaces normal to the axes. In the plane perpendicular to the direction of propagation we have the two stresses in figure 3.3. These are the only two possible quadrupole stresses: the stresses representable by all arrows pointing towards the origin (or away from the origin) are something like a fluid pressure, which has zero spin. The "stresses" (actually rotation) representable by all arrows pointing in a clockwise (or counter-clockwise) direction correspond to spin 1.
Answer
It is important to take these kinds of simple figures with a cube of salt. While they have some of the flavor of these creatures, they are too simple to "really be" about spin. With those caveats in mind, here are the figures:
Discussion
There are a sub group of physicists who lobby against visualizations. Give such people a piece of charcoal and a nude model, and they wouldn't know what to do. Feynman did do such sketches, and also developed diagrams that bear his name, much to the chagrin of his fellow Nobel prize winner Julian Schwinger. Just don't claim any of these are pictures of spin. Like all our other abstractions, the figures share some properties with spin, but not all.
Jan 2, Spinning the Interaction Story: Attraction and Repulsion (3 of 3)
Snarky puzzle
How would a ruling from the United States Supreme Court that mass had to be treated as -m instead of +m effect you personally or professionally?
Background
There are a few fringe physicists who want to flip the sign of mass. Others want to make it imaginary. Could the highest court in the land pull this off?
Answer
This Supreme Court ruling should be overturned. Since that is not possible under the United States Constitution, what needs to be done is pass a constitutional amendment that courts may not rule on physics laws. There are lots of physics laws that have an odd number of mass terms, so flipping the signs of mass would change how they act, not good.
Discussion
Not a great question, so it goes.
Jan 9, A Limited Toy Model for Classical Gravity
Snarky puzzle
Find a new constant velocity solution to the double O. Henry gravitational force equation. If you presume the same chain rule game, show the analytic solution has a 1/R - not 1/R2 - dependence. Do not share your answer with anyone looking for dark matter. Do share with people building models of stars in motion in galaxies. Don't expect them to be happy as much new programming will be required to test it.
Background
For a thin disk galaxy, the observed velocity profile starts at zero at the center, reaches a peak quickly, then stays flat. After the peak is reached, the velocity is not a function of R. The mass in the galaxy falls off exponentially as one moves radially out from the center (mass density is a function of R). Sounds like a word problem to me.
Answer
This one didn't pan out. A thin disk is not a sphere. One has to include the centripetal force. I think this needs a numerical approach, and I don't have the skill set for that.
Nothing to discuss.
Doug
MIT IAP classes, "Animating New Physics," Jan. 18-20, 3-5pm if a member of the MIT community and in Cambridge, MA. Otherwise, will webcast via Google+, http://gplus.to/sweetser
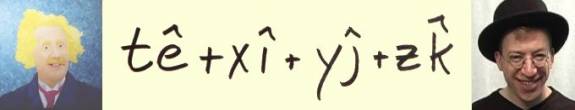



Comments