click or skip a reading of this blog:
April 18 - Higgs? We ain’t got no Higgs
The Snarky Puzzle
Factor B2 - E2. That should remind you of problems back in high school, maybe junior high, maybe first grade if you are Gauss II. Earlier in this post, it was shown how to make a gauge invariant combo of -E + B. When the order of operators flip, only terms with a cross product or curl change signs. Do that here. Crash the two gauge invariant quaternion 3-vectors to make a quaternion and Lorentz invariant scalar. Poynt to the meaning of the resulting quaternion 3-vector.The Back Story
I was preparing to give an Independent Activities Period class at MIT. So long as I could find a sponsor, I could ramble about whatever I wished. I gave a feeble effort to get the physics department to sponsor me, but they said their plate was already full. They suggested I ask the alumni association. Boy, were they great! The alumni association is used to being nice :-) They pointed out that the course should be something freshmen could take.
An MIT freshman will be a top notch high school student who likes math. I worked hard to make sure I didn’t skip any steps, having always hated the phrase “...and the rest is left as an exercise.” My motto: all steps should be small steps. My goal was to show them how to derivative the Maxwell equations from the Lagrange density using only small steps. One of the first ones is at the core of this snarky puzzle.
The Answer
The Discussion
Take the scalar of this term, plug that into the Euler-Lagrange equations, and out pop Gauss’s and Ampere’s laws. If you don’t know how, here are the baby steps and visuals (see “Derive the Maxwell equations and more” as a pdf or 4 half-hour videos).
The Poynting vector is the 3-vector that “just shows up”. On the wiki page, they talk about different people inventing this vector, one of those people being Oliver “I hate quaternions” Heaviside.
There is another Lorentz invariant scalar formed from only E and B fields. In preparing the lectures, I figured out why E.B is invariant. What one does is calculate the length of E-B and E+B, and subtract those two. The lengths of these orthogonal vectors will be the same, so the differences will always be zero. (Question: are E and B only orthogonal if there are no charges? I know I should know that...) Plug E.B into the Euler-Lagrange equation and you get the no monopoles and Faraday laws. I don’t think this is mentioned in Jackson’s “Classical Electromagnetism”, so it is not widely known these days.
The standard road to B2-E2 involves more work. One must know the rules of covariant and contravariant 4-vectors. Then there is the struggle to learn the opposite rules for covariant and contravariant 4-derivatives. Then one must keep track of these differences as a metric is used in the contraction step. In the end, you get a scalar, and you do not get the Poynting vector. Some will argue that it is good not to have the Poynting vector as it is not relevant to the calculation at hand. I prefer a complete story, so if the Poynting vector shows up naturally as part of a calculation. I take that as a good sign.
April 26 - Sexy Standard Model Symmetries
The Snarky Puzzle
Imagine a spacetime wire cube. No don’t, that is too hard. Do something simpler. Draw a square in three complex planes. Now imagine animating that. Got your picture in your head? Good, now Google for 4d wire cube and be honest about if your imagination matched reality.The Back Story
In a classic case of intellectual intimidation, students are told they will never be able to imagine 4D space. Not only is that true, but it is not relevant. We can all watch 3D space+time by being, breathing, and opening our eyes. The world has 3 spatial dimensions while the clock ticks on the wall. Spacetime is ordinary, not extraordinary.
I purchased Andrew J. Hanson’s “Visualizing Quaternions” soon after hearing the title. I realized I was in deep trouble when in chapter 4 “What are quaternions”, he wrote:
Equations 4.1, 4.2, 4.3, and 4.4 form the foundation of all concepts presented in this book
I had found errors of omission in those equations. The equations were not wrong per se, but by accepting the premises, so much visualization would be missed. He decided he had to work with only unit-length quaternions. This is a computer science guy, he should be able to deal with animations! Alas, my one effort to reach him by email got a null result.
He does have a 4D cube up on YouTube. That looks like a fancy piece of crap to me. Look at it spin and morph and change into a ladybug. No. A cube is a cube is a cube. No morphing, no twirling, hard right angles for all.
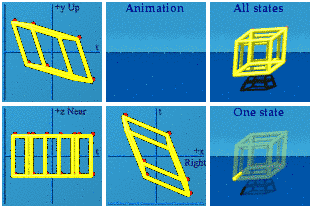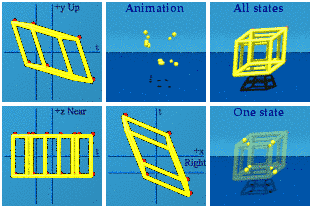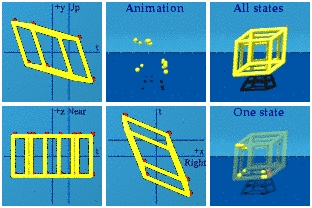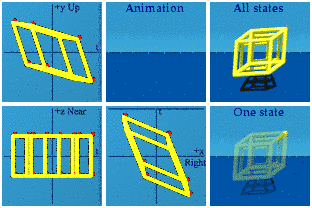
The AnswerThe straight on view:
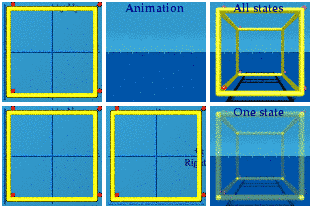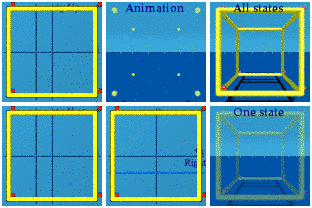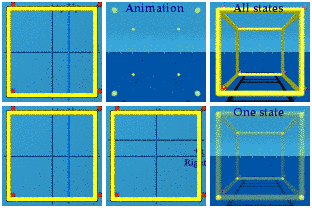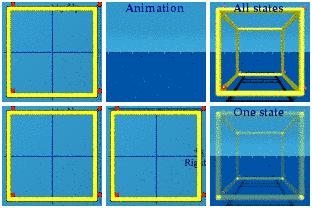Note: the red dots are the vertices, split into 2 groups of 8.After a 3D spatial rotation along the x and z axis:
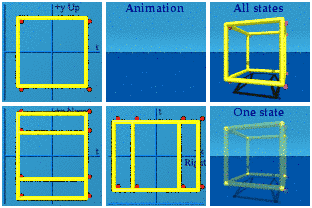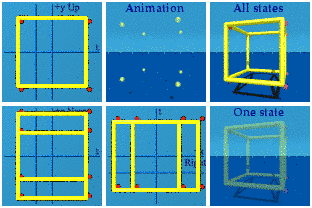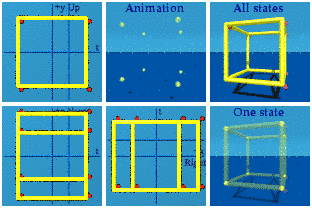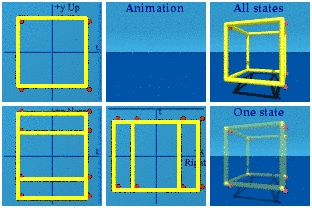
Nothing happens in the y or up-down+time complex plane. Two tennis courts or rectangles appear in the other complex planes. The animation still looks "blinky", the vertices split into 2 groups of 8.
Special relativity will tell the reader I have chosen a particular frame of reference, so that we get two groups of 8. Break up the simultaneity by boosting along x, xy, and then xyz.
boost along x only:
This has 4 sets of 4 vertices, whenever an edge-on square appears.Boost along x&y:
Looking at the zt or near/far+time complex plane indicates that there are 8 pairs of vertices.Boost along x&y&z
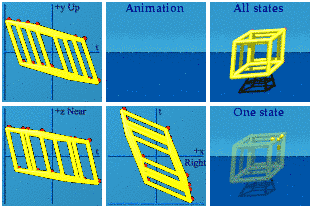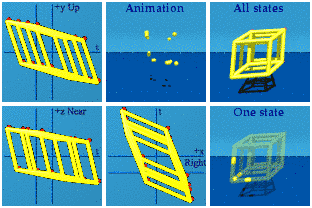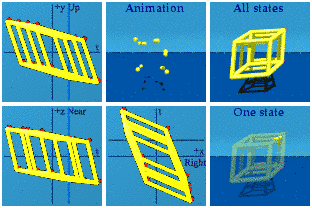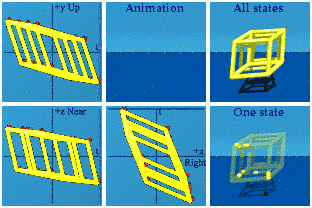Each vertex gets its own place in the Sun. Instead of blinking, this cube is like the spacetime box is being drawn from its -+++ position down to the +---. Different choices for the boost could draw from any corner to its opposite. The lesson here is to not read much into anything that blinks together. That is the sign of simultaneous events, so will be lost by a change in the reference frame.This answer was expanded due to David Halliday's prodding
The Discussion
I told a blind guy who emailed me about this animation I had about a spacetime cube. He corrected me, saying that I had a spacetime wire cube because it is only a wire cube that is mostly empty. Strange to be corrected by a blind man on a visualization, but it happened to me.
Analytic animations are transient. That is the hardest part to accept. The 3D cube we expect to see blinks into existence then disappears at times t=-1 and t=+1. The majority of the animation is spent transporting the eight vertices between those two moments in time. The vertices are traveling in time. The problem with the phrase “traveling in time” is people associate that with spookie stuff like traveling backward in time. We are all traveling forward in time. Flip through a photo album, and you are traveling backward in time: one week, one year, a decade, all depends on how old the photo or video is.
May 3 - Sexy Standard Model Symmetries 2: Experimental Corrections
The Snarky Puzzle
Be a flatlander. Imagine what it looks like if only 2 numbers are varied for the non-zero constant animation. Wear a bow tie to the celebration of your correct answer.The Back Story
I really wanted to find U(1)xSU(2)xSU(3) using only quaternions. This is the ultra conservative part of the ultra conservative fringe: say the things all the pros say. The unit quaternions are sitting in the middle of the standard model, that is the SU(2). I tell people quaternions are three complex numbers that share the same real. The group U(1) is a normalize complex number, so normalize a quaternion and three normalized complex numbers are guaranteed. I spent a few years dreaming about reaching out to the eight-fold way, SU(3).
The Answer
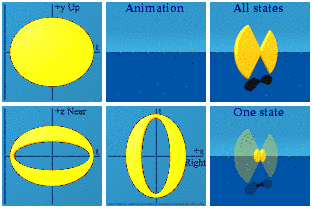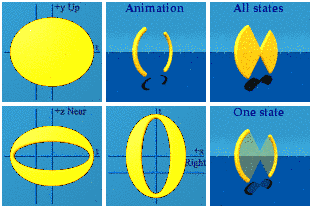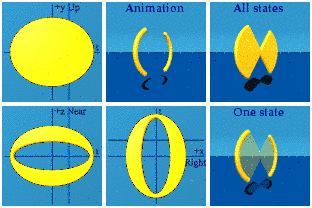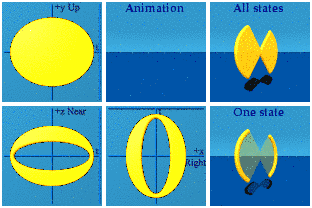
The Discussion
This bow tie is an artifact. It resulted from a limited range of the input: I chose random numbers from -1 to +1, not -infinity to +infinity. Like calculations, pictures can deceive.
What may have a longer term impact on my research was to give up my goal of getting the tensor products of the three groups U(1), SU(2), and SU(3). We know these symmetries must exist in a unified field theory Lagrangian so that electric, weak, and strong changes will all be conserved. What we don’t know about is the “x” in U(1)xSU(2)xSU(3), symbolizing the tensor product of these three groups. That certainly is the most natural assumption to make, but it is an assumption. As is my way, I will tack my sailboat a different way. All I need are the symmetries. So that is all I use. Notice that the group U(1) is a subgroup of SU(2) which is a subgroup of SU(3). If one writes a Lagrangian with SU(3) symmetry, it necessarily will conserve an SU(2) and U(1) charge.
It is understandable for people to dismiss such an observation. We prefer a world with separate buckets, this one for electric charge, this one for the three weak charges, and another for those strong charges. Different things deserve different buckets. The charge to being subgroups would make the charges too intimately related. The only relationship the three groups must have is that all are conserved. If one is conserved, they all are conserved, and they all are. All for one, one for all, as the Three Musketeers would say. This is the anti-E8 hypothesis, monster-minimalism.
May 10 - Gotta Get 16 Gamma Girls
[Update: new working title: Gotta Get 11 Dirac Gamma Girls +5 Doing an Imaginary Twist]
The Snarky Puzzle
At ICC8 in Campinas Brazil, I pitched the quaternions + California ring program to Prof. David Hestenes of Clifford&geometric algebra fame. Being a seasoned vet, this sounded like an old, bad dream to his ear. Quaternions are just a bit player, Cl(0, 2), in the larger sea of Clifford Algebras.[Note: see the answer for a problem with the question.]
The real numbers are Cl(0, 0) and a subgroup of quaternions. The complex numbers are Cl(0, 1) and a subgroup of quaternions. The gamma matrices belong to the Clifford algebra Cl(1, 3). [A transformation similar to gamma matrices can be represented with quaternions]. In an earlier snarky puzzle, I showed how to represent the Lorentz group using real-valued quaternions. Quaternions are intimate friends of 4π rotations needed for spinors.
Please list all the important things quaternions cannot do anymore.
The Back Story
My first international meeting was in Rome, focused on quaternions. I waited in vain for the second one to be announced. Every three years there was one for Clifford Algebras. I decided to go to The 8th International Conference on Clifford Algebras (ICCA8) and their Applications in Mathematical Physics (I am in the second row). I got to talk for a half hour, triple my usual time slot. The big draw was Prof. David Hestenes, the force behind geometric algebra (in the fourth row, a knight move away from me). One conclusion he has reached is that new efforts need to be made to educate students about deep lessons in geometry. I had reached a similar position, one reason for making so many YouTube videos and the command line quaternion animations. ICC9 is set to happen in July, but I cannot go due to responsibilities to the family which fortunately are cute and talkative at this stage.
The Answer
There is a problem with the question as posed.
The gamma matrices belong to the Clifford algebra Cl(1, 3)a fine statement...
and can be represented with quaternions.Not so fine. The Clifford algebra CL(1,3) means one and only one thing. It does not mean the quaternion triple product trick discovered and published by others. Perhaps I should have asked:
"The gamma matrices belong to the Clifford algebra CL(1,3), and their algebraic feats can be accomplished using a quaternion triple product translation table". That question decouples the jargon of the math machinery from what is done with these tools.
The answer to the modified question is a gravity field theory that can integrate with the other three forces of Nature. [Caveat: Mendel Sachs has done work to mesh quaternions and GR]
The Discussion
A metric is symmetric. Changes in a symmetric metric must be symmetric. Quaternions cannot do the job, but perhaps the California ring can.
Hestenes gave a thought provoking talk titled, “The Geometry of the Electron Clock.” It is a revival of an idea by Louis de Broglie. Even though life is hectic, I decided to watch the hour long talk. I was able to travel back in time and space to May, 2008 and hear his talk in Brazil. De Broglie views an electron as a clock. Plug the values in for an electron, and its frequency is a little less than a zepto-second (ten to the minus 21). Such a frequency has been seen in the lab. Hestenes explains it as as a rotating electric dipole. At time 58:13 you can hear me ask the final question about how his work would relate to the Higgs. He knows there is much more work to be done for his model.
In my GEM theory, there are all kinds of dipole solutions to the fully relativistic field equations. I was wondering what to do with the solutions. If an electron can both attract another electron with gravity and repel that same electron with electric charge, then maybe it should be viewed as a point dipole (that is not an oxymoron). If I were to work on the masses of fundamental particles, it would be this variation on de Broglie and Hestenes work.
If anyone is going to the 14th Eastern Gravity Meeting in Princeton, June 2-3, say hi.
Doug
Animation 1: q_graph q_graph -out 4D_wire_cube -box 1.1 -command 'generate_cube -stdout' -color yellow -command 'generate_cube -stdout -match 4 | uniq | q_add .1 .1 .1 .1' -color red -out 1.wire_cube
Animation 2: q_graph q_graph -out 4D_wire_cube_rotated -box 1.4 -command '221 -right "q_x 0 .8 0 .6" -left "q_x 0 -.8 0 -.6" "generate_cube -stdout"' -color yellow -command '221 -right "q_x 0 .8 0 .6" -left "q_x 0 -.8 0 -.6" "generate_cube -stdout -match 4 | uniq | q_add .1 .1 .1 .1"' -color red -out 2.wire_cube_rotated
Animation 3: q_graph q_graph -out wire_cube_boost_x -box 2.4 -command 'generate_cube -stdout | q_boost -vx .4' -color yellow -command 'generate_cube -stdout -match 4 | uniq | q_boost -vx .4 | q_add .1 .1 .1 .1' -color red -out 3.wire_cube_boost_x
Animation 4: q_graph q_graph -out wire_cube_boost_xy -box 2.4 -command 'generate_cube -stdout | q_boost -vx .4 -vy .3' -color yellow -command 'generate_cube -stdout -match 4 | uniq | q_boost -vx .4 -vy .3 | q_add .1 .1 .1 .1' -color red -out 4.wire_cube_boost_xy
Animation 5: q_graph q_graph -out wire_cube_boost_xyz -box 2.4 -command 'generate_cube -stdout | q_boost -vx .4 -vy .3 -vz .2' -color yellow -command 'generate_cube -stdout -match 4 | uniq | q_boost -vx .4 -vy .3 -vz .2 | q_add .1 .1 .1 .1' -color red -out 5.wire_cube_boost_xyz
Next Monday/Tuesday: Argand plane crash
Comments