This is a new title:

Gotta Get 11 Dirac Gamma Girls, Plus 5 Doing an Imaginary Twist

[Note: based on discussions below, I decided to alter the title from "Gotta Get 16 Gamma Girls". The core figure in the blog is not of the 16 gammas in the Dirac basis, but only 11 of them. 5 of them have an extra factor of i. I will have to consult a few articles on the subject to see how they handled this issue.]

I spent a year playing around with gamma or Dirac matrices in a relativistic quantum field theory class at Harvard. It was like being at the World Economic Forum at Davos, Switzerland, and thinking I got no money, no power, what am I doing here, outclassed in so many ways? No, I haven’t been invited to give a talk ever in economics or physics, go figure. I look back at the field theory class and scratch my head, what when on there? Calculations were done that match data to a point, then supercomputers have to take over to churn through all the permutations. Only the smartest of the smartest of the smart kids get it. Makes me wonder if they are bluffing.

By the end of this blog, I hope you can do 3 things. First, from memory, write down all 16 gamma matrices in a quaternion representation. I cannot do that with the standard gamma 0-5 and sigma combinations. Second, collect them into 3 distinct sets. Third, have a visual sense of what they are doing to a pattern of events in spacetime.
[click of skip this reading of the blog.]
Once Minkowski figured out special relativity was about 4D spacetime rotations, people considered quaternions a natural candidate for the job. The easy approach didn’t work, so they all decided to cheat and toss in an extra factor of i on top of the one already in use, but the second i commuted. In my own survey, all work on quaternions before the mid 90s used biquaternions. Yes, I know, they were not really cheating because they defined their rules clearly. I reply with the Knights of NEE, not elegant enough.

Stefano De Leo was working out of Lecce, in the heel of Italy. He wrote a series of papers showing how to use real-valued quaternions to do the heavy lifting of physics. For example, in 1995, he wrote “Quaternions and Special Relativity” http://arxiv.org/abs/hep-th/9508011v1, showing a way to get the job done with real-valued quaternions.While I was able to follow along, I was not able to write code for his proposal, so by the way I work, I didn’t get it. The important message was that it was doable with real-valued quaternions.

There are some advantages to owning quaternions.com. People presume I am a professor and sometimes want to discuss their own efforts in this area (who would do this just for amusement?). José Luis López-Bonilla of Mexico City got his Ph.D. in theoretical physics. He has four kids and now works for a telecom company. He sent me a two page paper. One cannot go in depth in 2 pages, but there was a great table that mapped one way to write the 16 gamma matrices with the one way to write the quaternion representation.

What is the one quaternion way? There are 4 basis vectors for quaternions, 1, i, j, and k. If there is a quaternion you want to go under the gamma-knife, pre- and post- multiply it by the basis vectors. There are 16 ways to do that, no more, no less. I bet you can memorize that because it is so simple.

Here is my rewrite of the critical information in José’s work (in collaboration with L. Rosales-Roldán and A. Zúñiga-Segundo, a translation between the 16 permutations and the sigma and gamma matrices [Note: this form has corrected 6 errors found in the original. Translating can be tricky.][Second correction: a title change and highlighting of the 5 factors of i was added.]
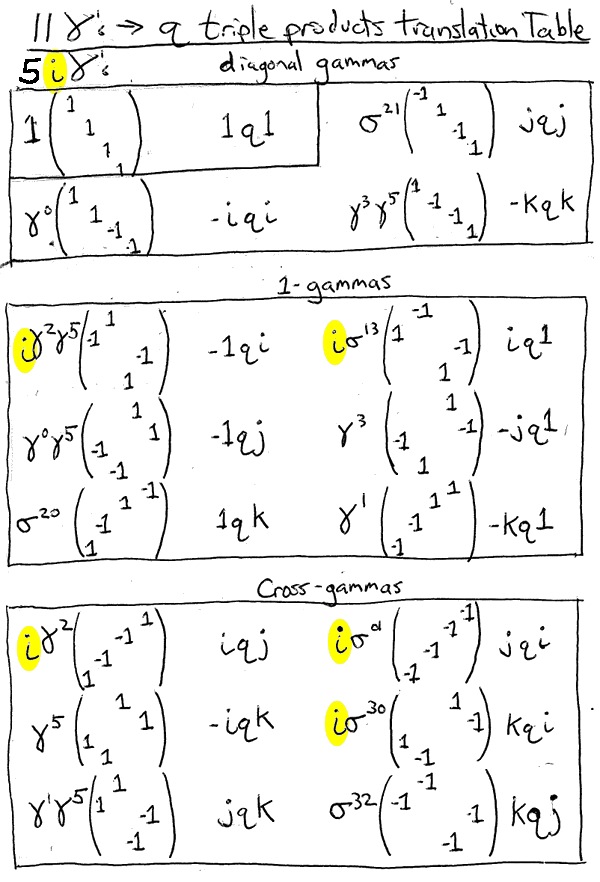
The most important one is 1q1. Classical physics, and classical quantum mechanics only use this one. It doesn’t change a thing. I like that :-)

What would a group like U(1) or SU(2) look like if I hit it on both sides with and of the 16 quaternion gammas? The animation would remain the same. There is a circle, there is a growing and shrinking sphere. I decided to play with members of the group instead of the complete set.

Here is an animation of an inertial observer, generated by adding the same number over and over again.

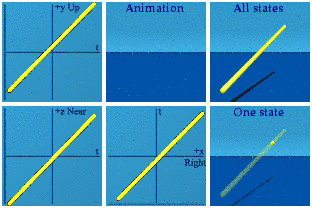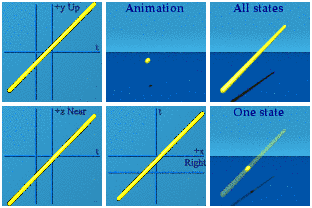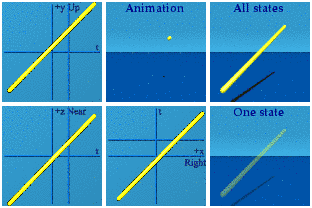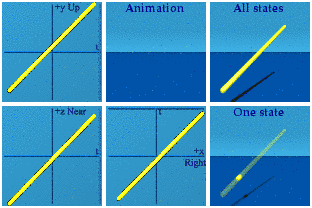
Not too interesting. Gammas come up in the context of the standard model, so I decided to map these straight and narrow events to an animated unit sphere by taking the norm:

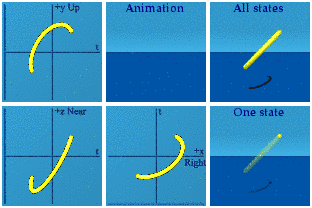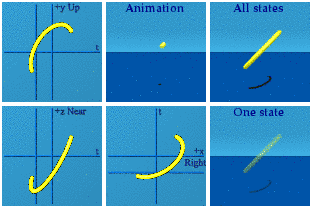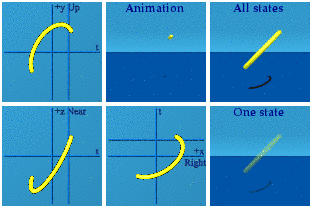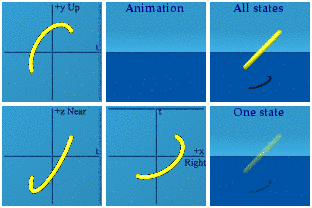
This is more fun. Every event shown has a norm of one. This collection of events starts with a pair running away from each other before one disappears. The long-lived event goes out, stops, and takes a step or two toward the origin before disappearing. The shadow underneath the All States graph shows it follows a curved path in space.

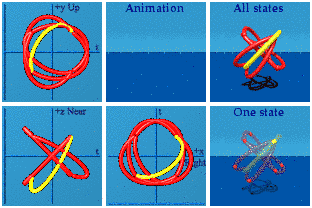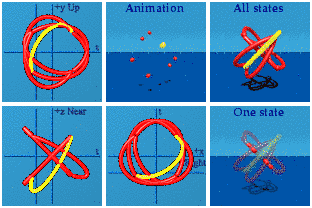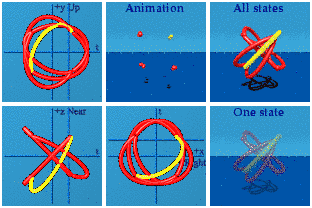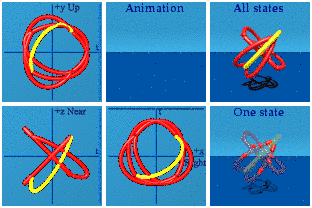
The next gamma quaternion matrices to consider I call the diagonal gammas, iqi, jqj and kqk. These at least put all 4 values back where they belong. For example:
i (t, x, y, z) i = (-t, -x, y, z)
Two terms flip signs, two keep their signs. Here is the animation of the diagonal gammas in orange:

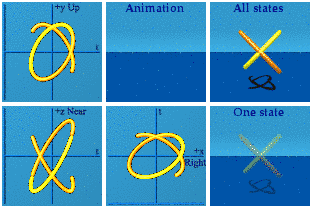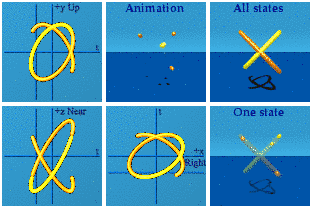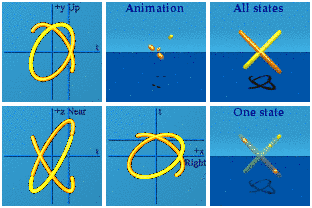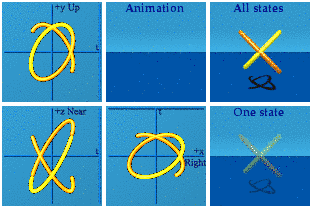
In each of the complex planes, there is one orange line that completes the oval, and another that is the time reversal of the input. If there are "completers", why does the yellow appear to be on her own? The 3 animated points are made up of one completer plus two time reversals:


In the Right/Left+time complex plane for this iqi animation, there is both a conjugate and time reversal. The double reversal completes the circle. In the Up/Down+time and Near/Far+time complex planes, only time flips sign. You can spot the time reversal quality if this is watched carefully. The first thing the yellow does is a 2 particle run-away until gone move. Look for that at the end of the animation of the orange one.

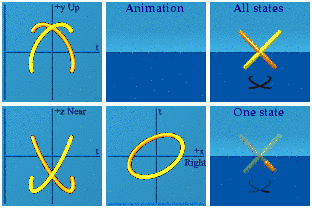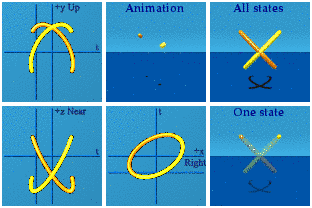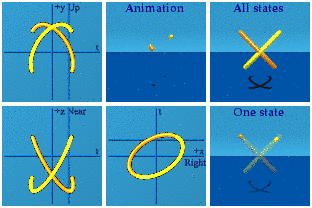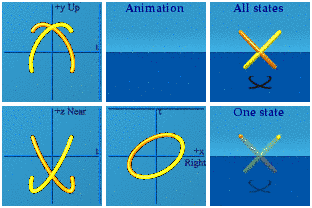
Call the next set the one-gammas. Information is getting systematically scrambled:
1 (t, x, y, z) i = (-x, t, z, -y)
Time and space switch chairs, tossing in a minus sign for the x. The y and z swap too, with y having to flip its sign. Here is the animation in red:

Three pairs are easy enough to spot. What is going on in the complex planes? No wonder the animation is not easy to get.

Call the final set the cross-gammas. These 6 have a pair of different imaginary basis vectors on the outside. 


These have the scrambled look of the one-gammas.

Put it all together:

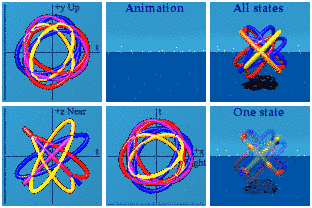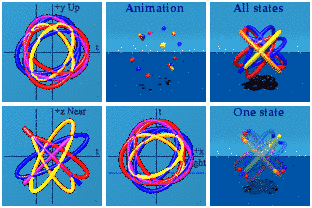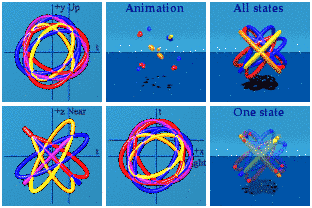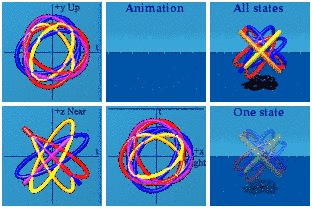
There is something to see here: four groups of four. The 16 gammas can take one path in spacetime and generate 15 other paths of events. The sum of all possible histories may look something like this. The animation has the look of relativistic quantum field theory: many particles at once doing things that I am probably not bright enough to understand.

Have the goals been achieved? First, write out all 16 gammas using quaternions basis vectors in a quaternion triple product. Second, group the 16 as diagonals, ones, and crosses. The visualizations at least provide a hope for meaningful animations in the future.

Doug

Note added in proof:
The initial 16 gammas to quaternion triple products had 6 errors. I had not used the translations in practice. As penance, I created a Mathematica notebook to confirm the data in the translation table. I spotted two missing minus signs on the gamma1 gamma5 matrix representation, but otherwise things were OK. If anyone is interested, the mathematica notebook and pdf are available.

The animations were generated with these commands using the command line quaternions software.

Animation 1: q_graph  -box 2.5 -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000' -color yellow -out 1.linear

Animation 2: q_graph  -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1' -color yellow -out 2.linear_normalized -box 1.2

Animation 3: q_graph  -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1' -color yellow -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1 | gamma -bb ii -bb jj -bb kk' -color orange -out 3.diagonal_gammas -box 1.2

Animation 4: q_graph  -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1' -color yellow -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1 | gamma -bb ii' -color orange -out 4.diagonal_gammas -box 1.2

Animation 5: q_graph  -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1' -color yellow -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1 | gamma -bb ei -bb ej -bb ek -bb ie -bb je -bb ke' -color red -out 5.one_gammas -box 1.2

Animation 6: q_graph  -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1' -color yellow -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1 | gamma -bb ij -bb ik -bb jk -bb ji -bb ki -bb kj' -color blue -out 6.cross_gammas -box 1.2

Animation 7: q_graph  -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1' -color yellow -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1 | gamma -bb ij -bb ik -bb jk -bb ji -bb ki -bb kj' -color blue -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1 | gamma -bb ii -bb jj -bb kk' -color orange -command 'q_add_n 2.9 3.1 3.2 2.8 -0.006 -0.0059 -0.0061 -0.0062 1000 | g_u1_n 1 | gamma -bb ei -bb ej -bb ek -bb ie -bb je -bb ke' -color red -out 7.all_gammas -box 1.2


Snarky puzzle: 
At ICC8 in Campinas Brazil, I pitched the quaternions + California ring program to Prof. David Hestenes of Clifford&geometric algebra fame. Being a seasoned vet, this sounded like an old, bad dream to his ear. Quaternions are just a bit player, Cl(0, 2), in the larger sea of Clifford Algebras.

The real numbers are Cl(0, 0) and a subgroup of quaternions. The complex numbers are Cl(0, 1) and a subgroup of quaternions. The gamma matrices belong to the Clifford algebra Cl(1, 3). [A transformation with properties similar to gamma matrices can be done with quaternions as discussed here.] In an earlier snarky puzzle, I showed how to represent the Lorentz group using real-valued quaternions. Quaternions are intimate friends of 4π rotations needed for spinors.

Please list all the important things quaternions cannot do anymore.


Next Monday/Tuesday:
Snarky puzzle answers 2