I got counter snarked. At the end of my blogs, I include what I call a snarky puzzle. If you can follow along with the technical parts of my blogs, a snarky puzzle is  suppose to be a playful but snide problem with a straightforward answer. David Halliday asked a question of his own which I will present after setting up the context.
click or skip this reading of the blog
My (retitled) post “Gotta Get 11 Dirac Gamma Girls, plus 5 Doing an Imaginary Twist”... stop, retitled? Actually, the software here doesn’t like retitling... [correction: the software did work the second time I tried]. I was reporting on a paper I got that used quaternion triple products to represent the 16 gamma matrices. In the details of the calculations, David spotted an additional factor of i in 5 of the matrices. Those pesky factors of i means that quaternion triple products cannot represent the Dirac gamma matrices. I thought that observation was so important that I put it in the title.

Let’s start over. My (retitled) post “Gotta Get 11 Dirac Gamma Girls, plus 5 Doing an Imaginary Twist” showed how to put quaternion triple products to use. One pre- and post- multiplies a quaternion by one of the four basis vectors. All the triple product permutations makes 16 in all. The most useful one is the one that pre- and post- multiplies by unity. Nothing like staying in place.

There are a few animations of these quaternion triple products in that blog. Since David pointed out the quaternion triple product permutations were not the Dirac gamma matrices, he pondered what might be some of the relationships between the two and Clifford algebras.

P.S.  "Snarky" Puzzle proposition of my own:  Find an isomorphism, if possible, between the matrices of the "translation table" (see Gotta Get 16 Gamma Girls) and either Cl(2,2) or Cl(3,1), or both.
Hint:  One only needs to determine which of the matrices map to basis vectors e0 through e3, such that all these basis vectors anti-commute with one-another, and all the other matrices are given by products of these basis vectors (up to a sign, at least).  Where, for Cl(3,1), the squares of all the basis elements, except e0, must be +1, while the square of e0 is -1.  While, for Cl(2,2), the squares of two of the basis vectors are +1, and the squares of the other two are -1.
If you have the above, then the square of the product of all these basis vectors (e0e1e2e3)2 will be -1 for Cl(3,1), or +1 for Cl(2,2).

My short reply is simple: I don’t know. What I will now do could be called numerology, playing with quaternion triple products, making an observation or two, but missing out on some over-arching theme. Here goes the techno-ramble.

David calculated the 16x16 multiplication table and included it in a comment in the thread. I was impressed! David was smart, he programmed a procedure to get the job done using gammas and sigmas. I wanted one of my own, but with quaternion triple products (no on here should be surprised).

While sitting through a few talks I did not understand at the 14th Eastern Gravity Meeting in Princeton, I was wondering what to do. Sitting in the back row, I could see a favorite option was to read email. Others worked on their own slides. Email is email, slides are slides, what to do, what to do. A 16x16 multiplication table? I realized that I could fold a piece of paper to accurately represent such a matrix. Even numbers are nice. So I folded my paper up neatly horizontally, then vertically. I started to fill in the 256 squares like a Sudoku puzzle. It really is like Sudoku, but with a basis of 16 elements. No one element can be repeated in the same row or column.

I went down the columns 16 times, filling in one triple product at a time, say iqi, written tiny since it was part of a calculation. I went across the rows 16 times, adding the same thing on the ouside, say the jqj row to make jiqij. I visited each of the 256 boxes to multiply out the two basis vectors on the outside, so jiqij becomes -kqk which I wrote larger. If the box had a diagonal gamma (the iqi variety), I left it alone. If the box had a 1-gamma (like kq1), the box was shaded gray. The cross-gammas (like iqj) had backward slants. If the product flipped signs when finding its matching partner over the diagonal, I tried to add an outline both boxes.

Here is the final result.

What was most fun was feeling like I was doing a real physics calculation during talks I would have zoned out on. I was able to summarize a few of the patterns.

David’s investigations used graph theory to look at parts of the structure. I had also done some graph theory with quaternions. The next step will tell you a lot about my background as a scientist. I decided to do the completely labeled graph for the multiplication table. I would not stop until the entire thing was done. Once done, I would then look for simpler patterns.

Here is the final result:

This was done with inkscape, and the svg file is available. It is every bit as dense with information as the multiplication table. The file has more than 25 layers, making it possible to focus on smaller subjects.

Let’s start at the other extreme. Here are the 16 vertices:

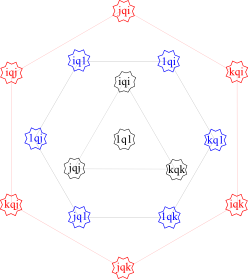
At dead center is the identity triple quaternion, 1q1. Surrounding that are the 3 diagonal gammas, always dressed formally in black. The inner blue ring of six are the 1-gammas because blue ribbons are given for first place. The outer ring are the red cross gammas.

If any of the sixteen are squared, this will result in either a positive or negative identity. The positive ones live in the diagonal and cross gammas.

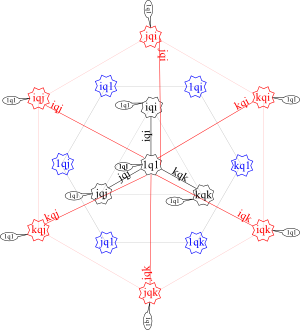
The squares that are negative all live with the 1-gammas.


[Correction: David Halliday pointed out that an earlier version had solid lines, but the correct version needs to have the dashed lines to indicate the sign of the label changes depending on what the start vertex happens to be. Going out from the origin requires the positive label, while going in requires the negative one as happens with quaternions.]
A few technical points. I have represented these as undirectional graphs because the label is the same no matter which way the product is formed (ii’qi’i = i’iqii’ = 1q1). Yet David pointed out that this is still has two directions. I don’t understand what sort of situation where this distinction makes a difference. Anyway, a solid line means a directional graph with identical labels both ways.

I have also included identity bubbles, the little loops with 1q1. That was unfortunate in a way, because without them, I could have called the positive identity graph K_1,9 or S₉. That stands for a complete graph that connects 1 central dot to 9 on the edge (K_1,9), making a star (S₉). The negative identity graph would be K_{1, 6} or S₆. I felt the little loops were necessary because I was using the identity. If one uses the identity, then show it wherever it can come into play. I realize that it is common in graph theory to not include them. The loops can make simple graphs no longer simple. Being complete is more important to me than simple. The big messy graph would be called K₁₆ if I did not include the little identity loops.

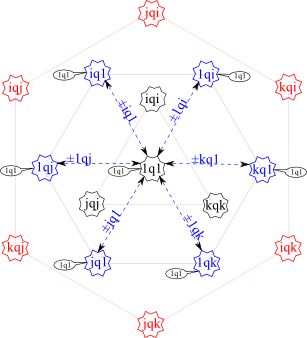
The graph for the diagonals with the identities shocked me.

OK, this won’t shock many, but I wrote a blog about it already, Quaternions For A Third Grader. This is the graph for the Klein group. I did NOT expect it to show up in this exercise. I started to use this graph in a quest to characterize the symmetric metric changes caused by gravity.

[Correction: David Halliday pointed out in the Snarky puzzle 2 blog that while this graph looks the similar to the Klein 4-group, it definitely is not. The reason is that there are 6 distinct labels for this graph, while the Klein 4-group only has 3 distinct labels. I will be researching that difference in the coming weeks and months.]

The next level out are the 1-gammas. Here are the directional graphs with the shared label.

This is the graph K_3,3 which has a name, the utility or Thomsen graph, [Added observation: It took me a while to see K_3,3. I had to ask a question over at http://math.stackexchange.com. Someone pointed out that if I exchanged the left and right most vertices, the resulting graph would look like the standard one written for K_3,3. There is still is something subtle going on once labels are added.]

 The graph is toroidal, meaning it fits nicely on a torus. David had spotted this property in his own explorations.

There are edges where the sign flips going one way versus the other. I used a dashed line and double-headed arrows for those. Here is the anti-symmetric 1-gamma multiplication graph.

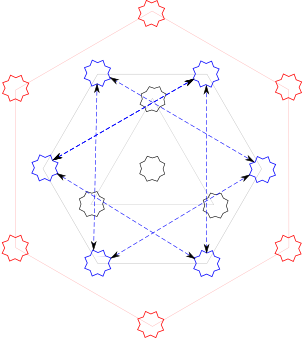
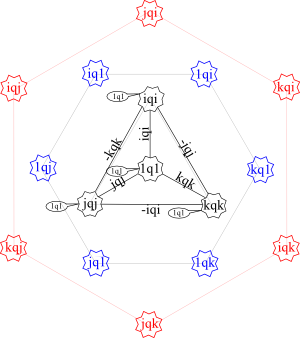
One can see two separate triangles, 2 K₃
[Additional graph suggested by David: combine the 1-gamma antisymmetric with the relevant identities:
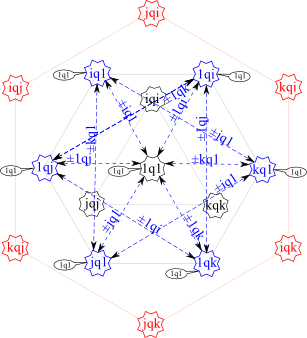
This looks like 2 quaternion graphs to me. That makes sense since one side is the identity.]


Combine the two K₃’s with the K_3,3, and one gets K₆.


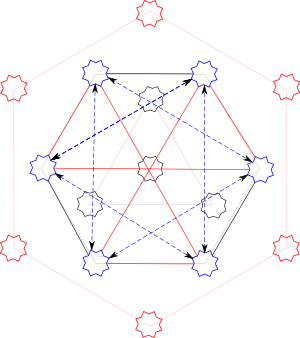
If I had studied any graph theory, I might have known this already.

The cross gammas also have the utility graph, K_3,3. [Correction: While the graph below does have 6 vertices and 9 edges like K_3,3, I do not see how to separate the vertices into two distinct set that all interconnect with the other set, which is the definition of K_3,3. This graph might not have a more familiar name.]


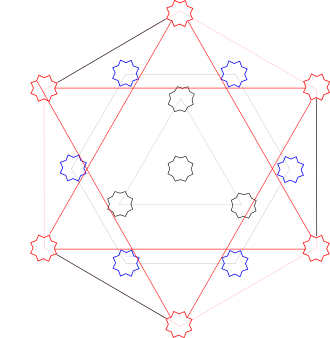
[Additional note: Someone on math.stackexchange.com pointed out this is the prism graph Y₃. I am nor sure of all the implications of that statement.]

The anti-symmetric gamma multiplication graph connects all six.

This graph is called C₆. Some introductory graph theory book probably explains why combining these two makes K₆.

We can form other complete graphs between the diagonals and the 1-gammas.

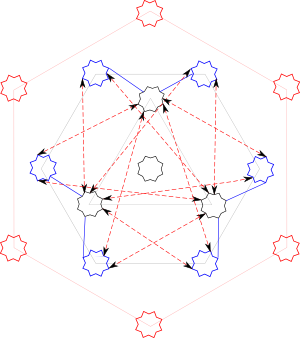
This is K_{3, 6}. Another K_3,6 is between the diagonals and the cross-gammas:

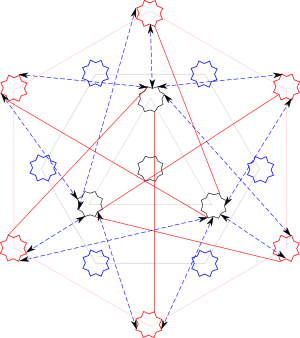
I don’t know if these two are technically different, an issue to address for someone skilled in the graph arts.

Finally, there is a K_6,6 for the 1-gammas and cross-gammas.

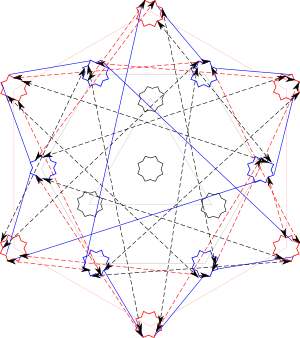
Will stop this numerology exercise there. I plan on repeating this work with clay and pipe cleaners which might take some time.

Doug

Snarky puzzle mystery. Usually I know the answer. This time I don’t. That will make writing the answer harder for me, but I doubt you care. I went way out on a limb to embrace something I have called California numbers. Being from the East Coast, I have trouble doing that. I have a friend who lives out there who is into the barefoot running revival, wearing these “shoes” that have individual places for each toe. In this blog, generated the California number multiplication graph using only quaternions. See if numerically you can show the two are the same: California numbers or quaternion triple products. If this can be done, I can stay on the East Coast with the division algebra quaternions.

Next Monday/Tuesday: Snarky Puzzle Answers 3