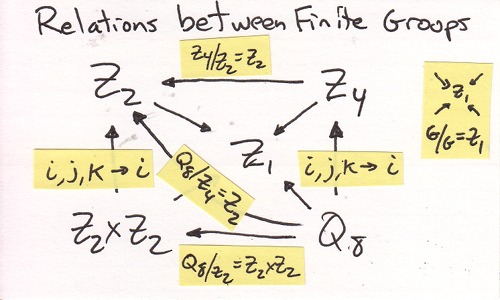
March 20, A Toy Model For Q8
Snarky puzzle
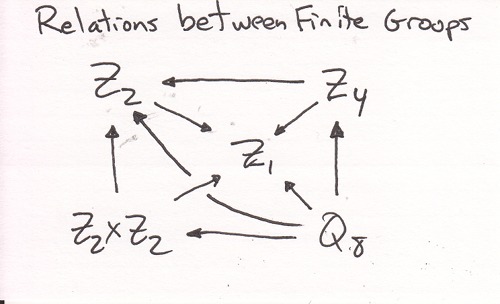
What is required so that a system undergoing change can be described just as accurately by the group Z4 as by Q8?Background
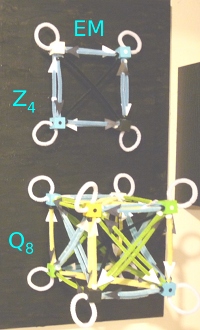
The funny thing I realized by building a pipe cleaner model of Q8 is that is too complicated. There must be a simplifying principle out there...
Answer
There are 6 planes that cut along the diagonals of the faces of the cube. Choose any one plane. Now delete the other four cubes not in the chosen plane along with their pipe cleaners.
[CORRECTION: The plane MUST be of vertices and edges that are all of one color, just like the Z4 image. There are only 3 such planes out of a possible set of 12 planes that have 4 cubes. Z4 and Q8 over the real numbers are the complex numbers and quaternions respectively. A quaternion has 3 complex subgroups.]
Discussion
Three of the planes have the two real vertices, -1 and +1. The other three are cycles of the three imaginary vertices. I hope to file that observation away and use it someday.[Clarification: the ones with -1 and +1 are groups, the others are not.]
March 26, Quaternions, THE Numbers of the Universe
Snarky puzzle
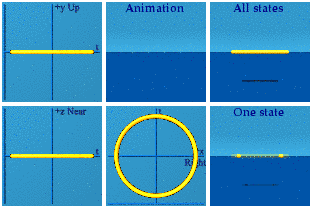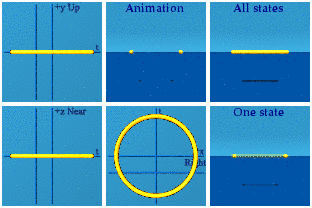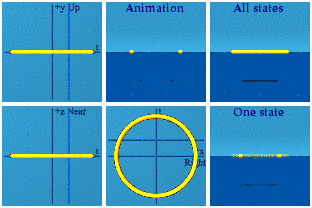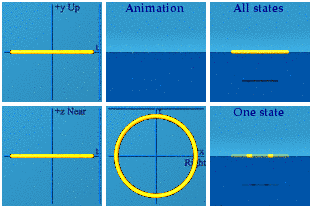
Is an animated circle symmetric in time? Is it symmetric in space?Background
A deep idea in physics is that valid statements should be true no matter the choice of coordinate systems. One fun property of the animations is how they don't reveal what coordinates are being used. In fact, I don't even include any axes in the animation.
Answer
Space reversal is indicated by a pair of points in all places but the origin. A pair of points appears throughout the animation. Time reversal is viable by remembering if how the animation started was how it ended. That is true of the circle animation. The circle is symmetric in time and space.
Discussion
If something is symmetric in time in an action, then it conserves energy. Why? The right answer to give one's grader is a theorem by Noether. The visual answer is if a system ends like it started, that will conserve energy.
[Essential clarification: the circle above does not conserve energy close to the origin. After all, there was nothing, then things moving having both energy and momentum, then back to a state of nothing.]
If something is symmetric in space in an action, then it conserves linear momentum. Why? The right answer is again Noether's theorem. The visual answer is momentum cancelled out the entire time, so never changed.
[Similar clarification: The two particles have momentum where there was none before. Far from the origin, momentum in the system is zero.]
April 2, The Little Gauge that Could
Snarky Puzzle
Fill in as many arrows as you can.Background
One open mystery is how Nature does the four fundamental forces all at once. In the standard model, three of the forces are equals, connected together as tensor products. Sounds like a shallow link, since one can imagine a Universe which used different groups. I dream of the day when our understanding means there are no choices about what is the structure for quantum field theory. A man can dream...
Answer
Discussion
What surprised me in this answer were similar paths for top and bottom, and for left versus right.
April 9, Cycling Around Z2
Snarky puzzle
Redo the Z2 pipe cleaner graph with blue in place of black. Comment on how that difference is trivial. Comment on how the difference is critical. Comment on how hard it will be to sell these two equations to the same buyer:Background
What is in a label: everything and nothing. Physics uses clear contradictions to its advantage. Is it a wave, continuous, or a discrete particle? The complete answer is both.
Answer

Discussion
The color of the pipe cleaners doesn't change any of the algebra. Yet the blue could be all about space. For someone who animates equations, the positive real numbers will be in the future. The negative real numbers are in the past. That is a reasonable way to look at Z2. But Nature is more exhaustive in her complete use of information than that. All it takes is two rules for the square of an imaginary basis vector.
March 12, BFF with HBT (hyperbolic trig)
Snarky puzzle
Show that addition of rapidities is the same as the velocity addition rule with the triple product. Don't ask me for help, I don't know the answer yet, but it sounds like a well-formed question.Sorry, I am too tired to figure this one out.
Doug
Next Monday/Tuesday: 24 Steps to The Precession of the Perihelion of Mercury.





Comments