The idea for this blog was dead simple. In my second blog at Science 2.0, "Quaternions for a Third Grader",  I showed of my clay and pipe cleaner model of quaternion multiplication. A few months ago, David Halliday and I started talking about the finite group Q₈, which over the real numbers becomes the quaternions. David pointed out my tetrahedron was half the cube it needed to be to represent Q₈. That was the idea for the blog: make a cube to represent that finite group.

It was quite the challenge to make the tetrahedron out of clay an pipe cleaners. The structure is rather fragile. A few preliminary sketches of the cube indicated that each of the eight vertices would need 14 holes drilled. Clay was not up to the task. The more precise I could be, the better chance the result would look like a cube. After wandering the aisle at several craft stores, I saw ¾" wood cubes. That could work if I could drill precisely. How does one drill at an angle? Buy an angle clamp at Sears.



When doing an upgrade to a piece, it is not enough to improve materials. There also needs to be a filling out of the concept. What has been most interesting in the discussion are the relationships between Q₈ and the groups Z₂, Z₄, and Z₂xZ₂. I decided to make those too, and include them so one could see the connections between them all.

This one image required I take a vacation day from work, but I do have something new the wall:







[Correction: The initial images had Z₄ with only 2 vertices instead of 4.][This is now version 3, where I was able to find the errors in arrows found in Q₈. The system was direct: do one simple arrow, and the rest follow because they must flow around a plane defined for a given color. Consider the two planes defined by Kelly green pipe cleaners:



The positive k's go one direction, the negative k's go the other. That was an easy data quality system to implement. I made mistakes on 6/48, or 1/8.
I could release a version 4 since I spotted another error. I was wondering what other kinds of checks I could do. One is to count arrow heads going into a cube. Three should be white, three should be black at each of the eight cubes. A 2/4 split indicates an error. That is not a test people on the web can do. Here is another test: for any face, one set of the the two arrow heads on parallel lines must point together, the other two must point apart. On the top, all point together, so there is an error. The yellow (+j) needs to be flipped.]

It became important to me to include the trivial group. Why? When a physicist says: "I am studying foo interacting with bar." What that statement does is define the trivial group. They will start with foobar and end with foobar. Another good reason to keep the trivial group is that it can be seen in all the other groups. Every group has the 1x1=1. I call that the "slacker" operation, the one that keeps going by doing nothing. It is vital to acknowledge the slacker that is mostly a good description of systems.

Another big insight I obtained was to spot the relationship between quaternions and complex numbers. Sure I have known that quaternions have three complex numbers as subgroups. This time I can see the cube getting squished and flattened until Q₈ makes a transition to Z₄. This could happen if only one spatial parameter matters in describing a system. Sure, the other two dimensions are there, but they don't matter in the description of the system.

There is another type of squish, going from Z₄ to Z₂. That represents a move from a directional graph to an undirectional graph. 

[Correction: Z₂ can be seen in Z₄ by deleting two fo Z₄'s elements. Not much of a squish.]

Every representation is flawed. The biggest issue with this is the image is static. I will update this blog Tuesday night with dynamic versions of these graphs.

[animation update]
Do the black pipe cleaners first, those that go from -1 to +1, -i to +i, etc.


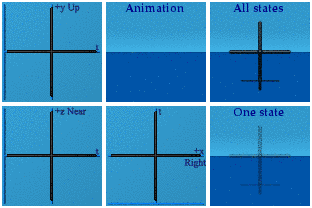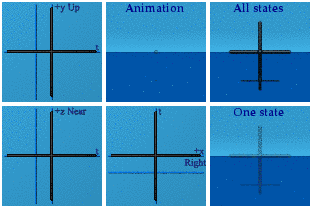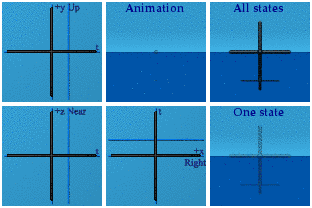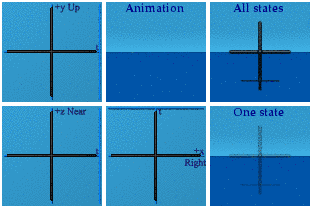
All the points are center stage.

The blue pipe cleaners diversify at least in the tx plane:



A similar pattern holds for yellow and green and their corresponding planes:





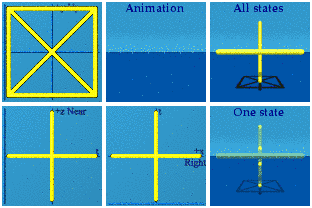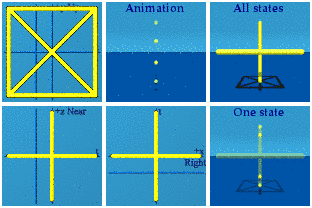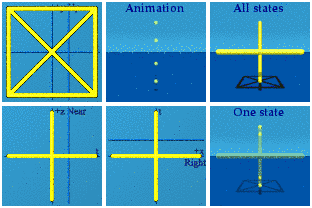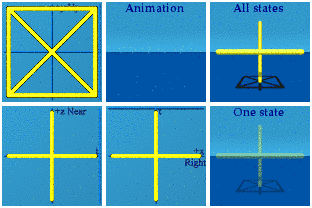
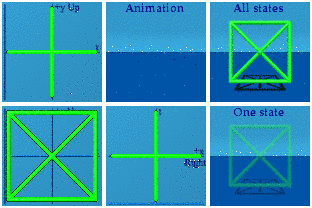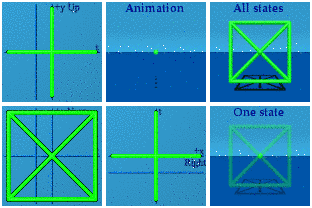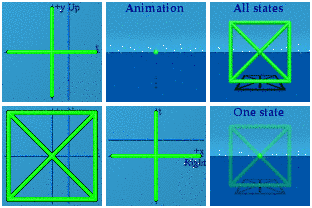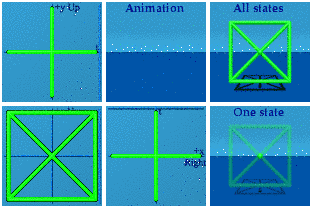
And of course, these can all be combined to make an animated version of Q₈:



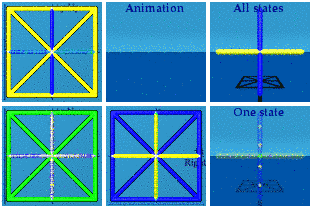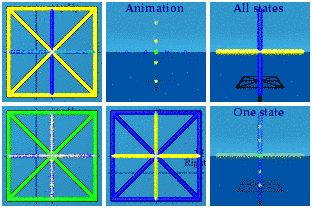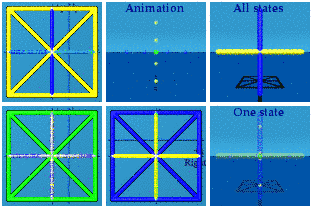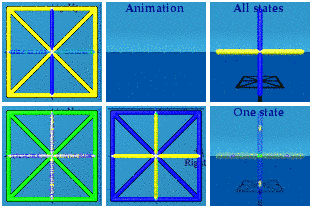
Like the pipe cleaner static model, it is not easy to see what all is going on here since there is much overlap. There are three "blink" times: -1, 0, and +1.
[end update]

Doug

Snarky puzzle: What is required so that a system undergoing change can be described just as accurately by the group Z₄ as by Q₈?

Quaternion Jam session: Saturday, 11AM on Saturday, Google+ Hangout.

Next Monday/Tuesday: Quaternions, THE numbers of the Universe[title for an Ignite Boston talk I will give on Thursday, March 29]