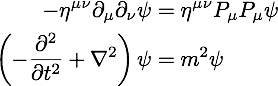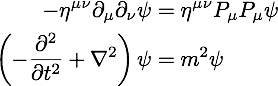 Bell's Future Quantum Mechanics - A Novel Interpretation
Bell's Future Quantum Mechanics - A Novel InterpretationHello! Years and years have gone by without a blog. For reasons I do not understand, I appear to...
 Future Train Wreck: Mine or Modern Physics talk Next Thursday, Jan. 26
Future Train Wreck: Mine or Modern Physics talk Next Thursday, Jan. 26If you are in Cambridge, MA on Thursday, Jan. 26, you can see me live at MIT in room 3-270 from...
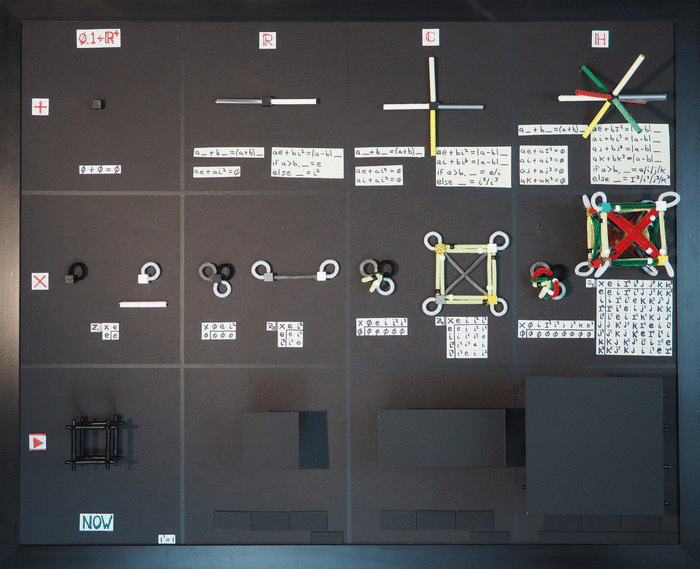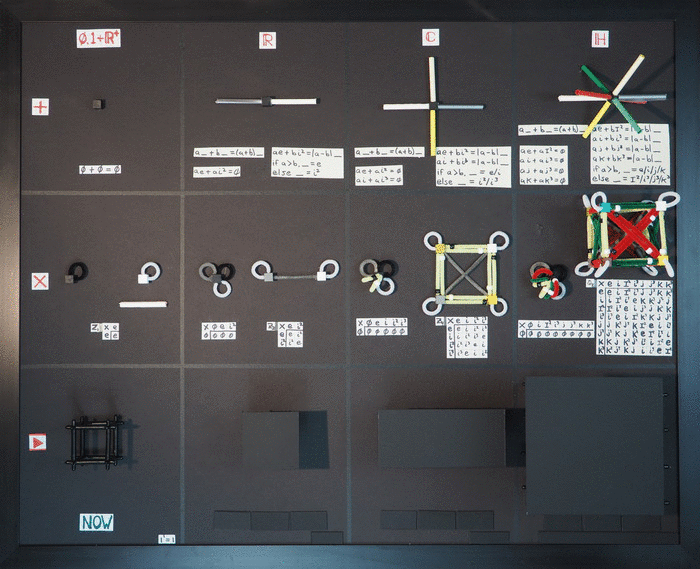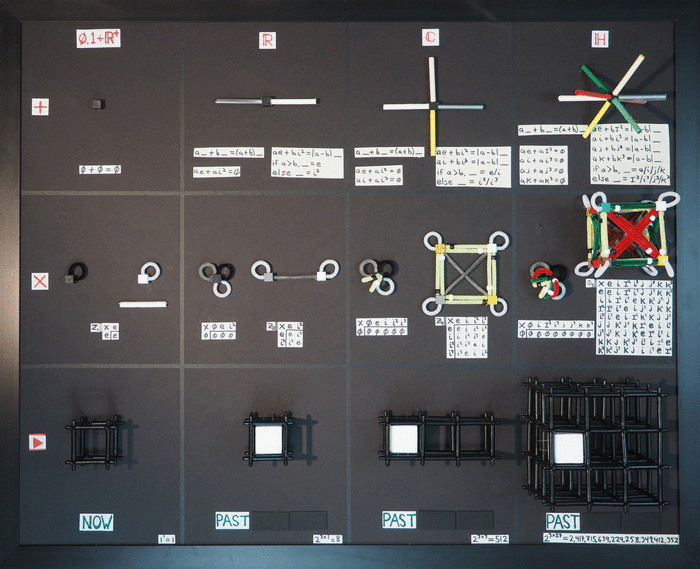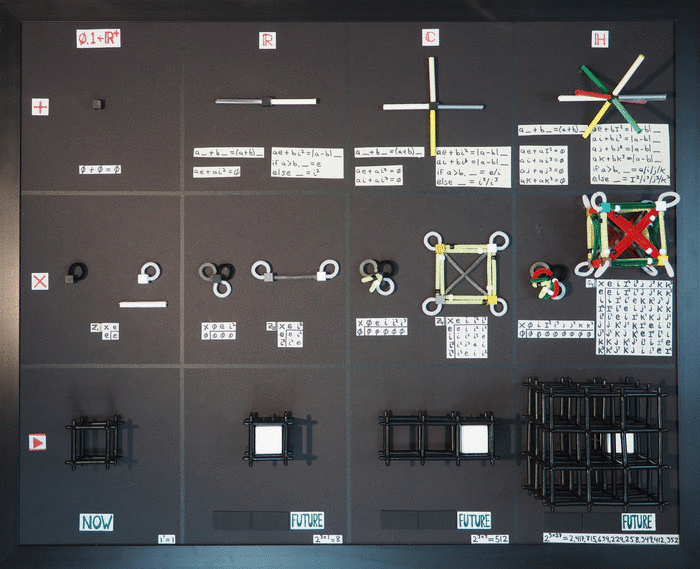
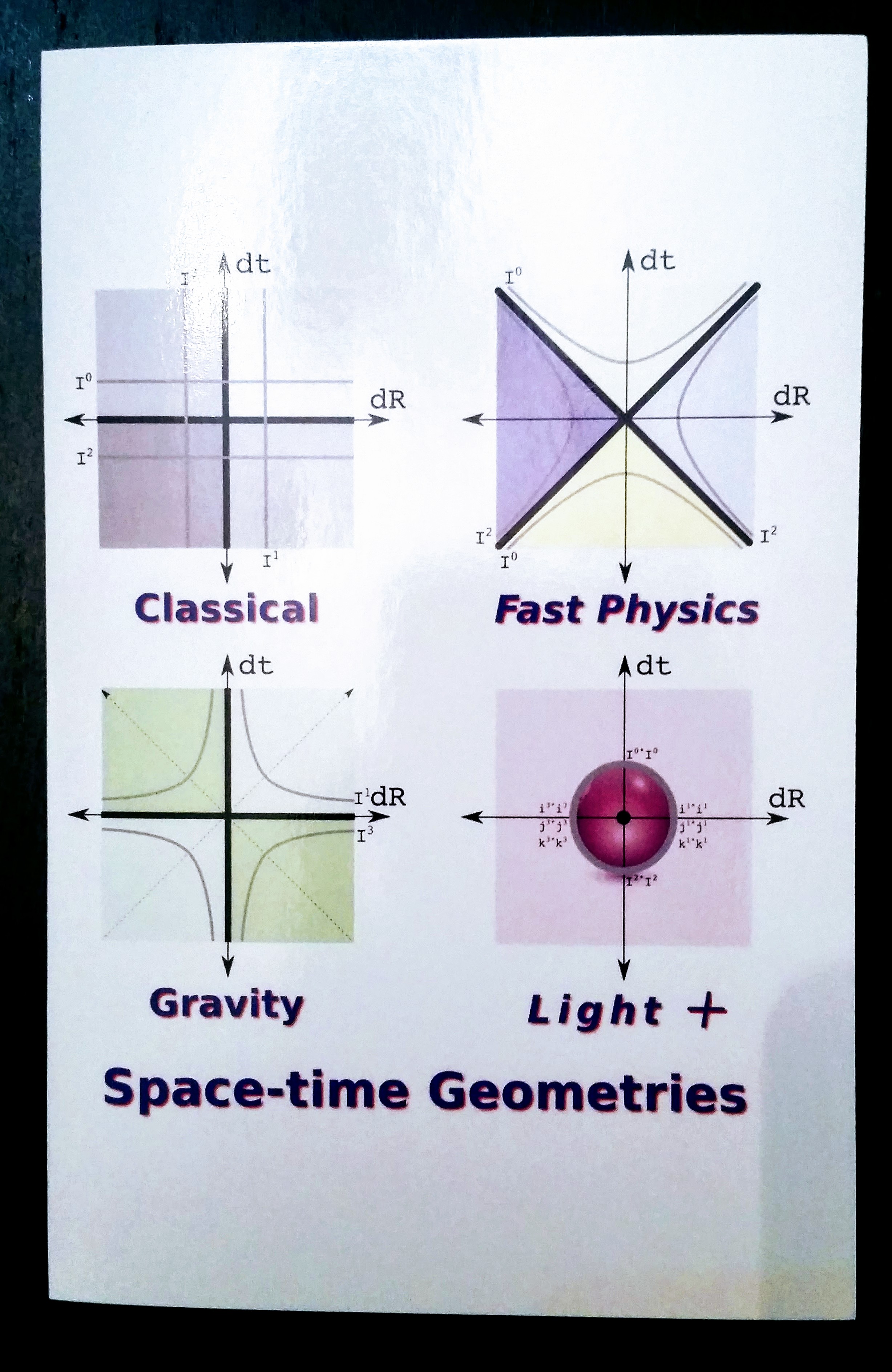 Holiday Physics Card, 2016
Holiday Physics Card, 2016Just put them in the mail on December 24...It was a fun year of thinking, whether the idea is right...
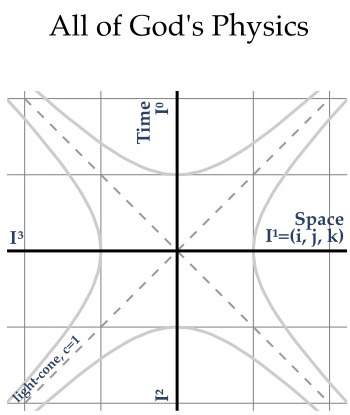
I gave a 15 minute talk at a local Americal Physical Society Meeting. Here is the title and...