[Update: as a commenter pointed out, here is the actual talk.
The title of each slide will be written in bold. I read a book on presentations that recommended most slide titles should be sentences, so this transcription of a future talk is easy, no wormholes needed.
Quaternions, THE Numbers of the Universe. The title may be true someday. I am leading a nascent open science project to see if the title is true.
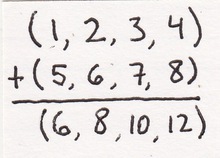Quaternions are numbers with four parts.The numbers can bee added, subtracted, multiplied, or divided. That is both ordinary and a bit odd. Let's find a real-world example of this kind of time and space addition.
We are here now. Add 6 hours and various paths, and all here now will be asleep. Both time and space are added together to make a statement about a future place.
Blame the Greeks with their search for permanent perfection.
This is pre-Euro zone, more like 300 BC. Axioms, postulate, and proofs were both a great advance and a tight straight jacket.
Euclidean lines are straight yet Nature is full of odd lines.
Fractals are the math of rough. It was a tough project to sell the idea of fractals to professional mathematicians, even though Benoit Mandelbrot was every bit the pro.
Geometry is permanent, yet everything is temporary.
We need the math of transience. Time should not be treated as a tacked on parameter. Instead it should be in the center of the algebraic stage. I hope quaternions are up to the task.
Quaternions have a horrible rep that continues to this day.
"Quaternions...though beautifully ingenious, have been an unmixed evil to anyone who have touched them in any way, including Maxwell."Some people today would include me on such a list. I prefer my evil unmixed. Nothing like being bitch slapped from the past.
--Lord Kelvin
Quaternions are a one-trick pony for doing 3D rotations.
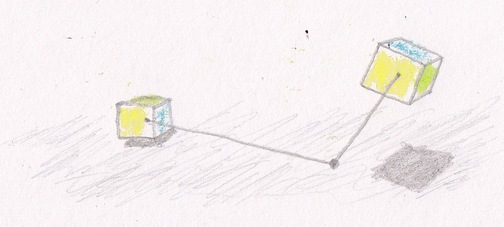
Great for games and rocket science, but they cannot do a Lorenz boost* which is a technically solid reason enough to never use them for a serious calculation in physics.
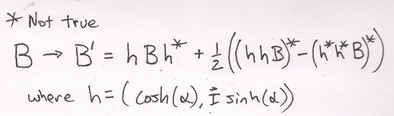
Quaternions are magic math. Square one and sees the square of the invariant interval of special relativity.
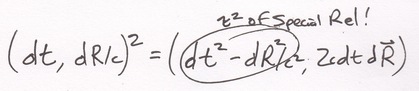
Take a simple derivative and see the fields of EM:
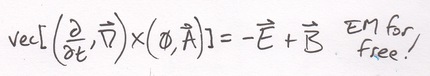
"Get your [interval] for nothing, and the [fields] for free" to misquote Dire Straits.
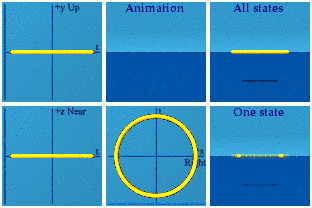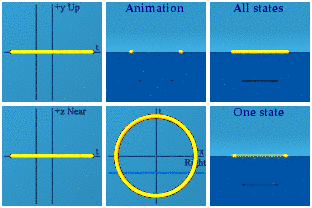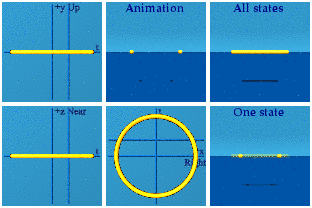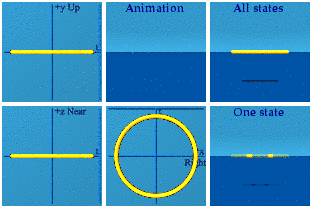
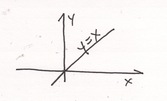Analytic geometry is math making a graph. This is a real simple graph, the venerable straight line. It is a static graph that is exclusively about space.Analytic animations is math making a movie.
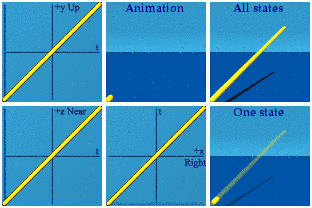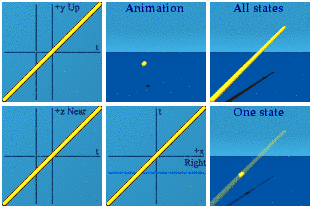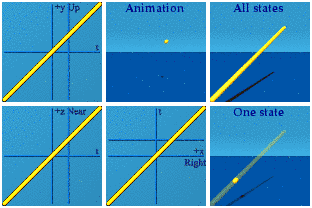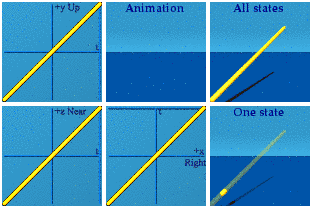
A dull but dynamic image about spacetime.
Time reversal requires one to remember.
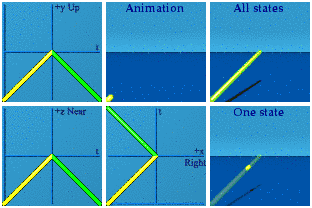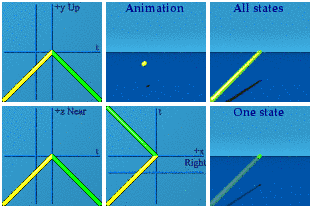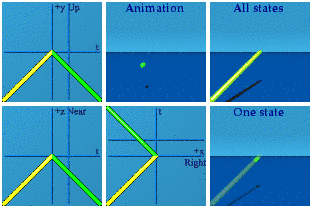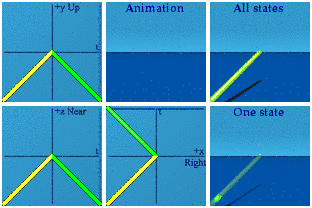
Time sits in the real number position of a quaternion. Real numbers are time in the analytical animation representation.
Space reversal requires a mirror reflection.
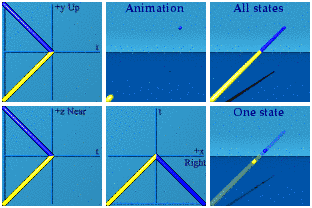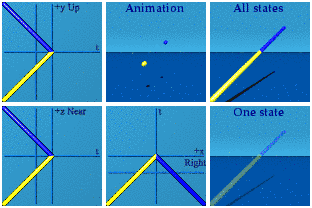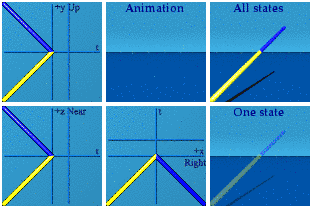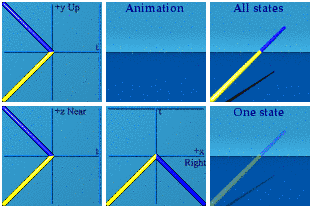
Imaginary numbers are about 3D space.
The difference between real and imaginary numbers makes sense. Compare the two animations above. No more need to reference the square root of -1.* Using one's memory for real number reversal versus a mirror just looks different from the mirrors required for imaginary number sign flips.
* The square root of -1 truism is still true. The Argand plane is still true. I found the 90 degree difference between the real and imaginary axis to be both useful and hollow at the same time. For me, the animation representation of the same algebra makes more sense and feels solid.
Time AND space reversal can look like the future.
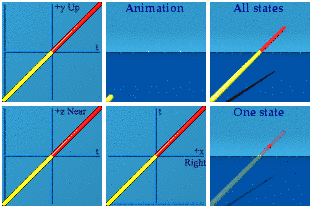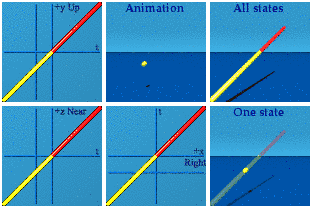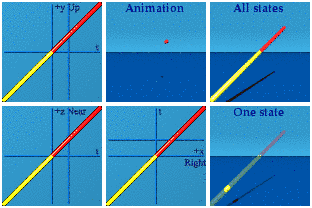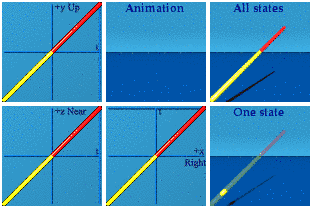
Think about the red line being both a reversal in time and in space of the yellow line while smoking some weed. Please do so under medical supervision.
Most of my time is spent on a new field theory for gravity. I call it a failure in progress :-) I have been able to derive the Maxwell equations using quaternions, something Maxwell himself wanted to do. I still have hope for finding a legal variation on Max.
Blog Monday night on Science20.com. And it usually creeps into Tuesday morning.
The blogs get a thousand reads a week, a factor of 20-100x of the lead bloggers on the site. The work has worth it since it provides a good source for critical feedback.
A small group is working on this topic without funding. They hail from the US, UK, and Australia. The sparse group was recruited from investments I have made on the web. My YouTube videos have generated 235k downloads. Quaternions.com is on the first page of lists for the word for four Roman soldiers as found in the King James Bible. VisualPhysics.org has all the Drupal tools for a community, just not the people.
Quaternion jam sessions are on Saturdays at 11am Eastern Standard Time. It is a Google+ Hangout.
I hope to see some of you there.
And that should do it for the 5 minute talk... It will be interesting to see if I have made it too technical or not, how much info can be shared with such a crowd.
Doug
Snarky puzzle: Is an animated circle symmetric in time? Is it symmetric in space?
Google+ hangout: Saturday, 11AM
Next Monday/Tuesday: The little gauge that could
Talk Report:
The Ignite Boston 9 event was a good way to spend an hour and a half, so long as you don't mind wild shifts in subject. Some have complained about the shifts within my own talk, but in a way that fit with the theme of the evening, which there wasn't one except these were subjects the presenter cared about. The first talk was about history, who owns it. There was a talk about making buildings adjustable for different uses. A cute robot captivated people for five minutes. One person focused on revolution. Naturally there was a talk about using GPS units to map towns in Uganda.
Five or six people gave me positive feedback. That must be taken with a block of salt as negative feedback after a talk is rare unless it is on a cultural flashpoint, which recruiting people to work on quaternions is not.
This talk represented marketing work. I passed out all of 1 business card. I am not a good pitchman since I point out flaws. I still consider it a success because one cannot know what secondary or tertiary conversations might happen because I was one of the dozen or so people who stood up in front and talked for five minutes instead of the two hundred (estimated) in the crowd. The talk was recorded, so will have a web life that is not predictable, but probably will not amount to much.
The moderator kept pitching us to eat the pizza, but there was not much mingling (not that I am good at that either). I did have more conversations about the subject than happens at an early morning APS meeting.
I am keeping the day job, but it was worth the effort.
Comments