Scalars, Vectors, and Quaternion [Scalars and Quaternion Vectors]: Definitions (1 of 2)

More Articles

About Doug

Trying to be a semi-pro amateur physicist (yes I accept special relativity is right!). I _had_ my own effort to unify gravity with other forces in...

View Doug's Profile

Doug Sweetser

[Clarification: I tweaked the title because the focus of this blog was intended to be quite small. While scalars and vectors are used in a dizzying array of areas in many dimensions, quaternions are constrained to work in one plus three dimensions. One could say one plus three equals four, which is true, but I say one plus three because with quaternions, the one has different math properties from the three. What happened in the comments was the first two folks admitted they were looking for a blog with a different subject, one that might have me linking quaternions to objects that transform like 4-vectors. That really is beyond the scope of this blog which doesn't confront how anything transforms. I will edit this blog and my comments to clarify when I mean quaternion scalar and quaternion vector because any and all quaternions are the combination of a quaternion scalar with a quaternion vector. Those words have no implications for how a quaternion transforms.]

Scalars and vectors, dot and cross products, div, grad, curl and all that are old friends, defined in the first steps to more than one spatial dimension. In this blog, those definitions will be reviewed. The familiar will be compared to quaternion products where all of these structures were first seen. Yet the constraint that quaternion products remain quaternions puts an odd slant on our familiar friends.

Scalars are the numbers we first learn about. The numbers of blocks is a scalar, as is one's weight on a scale. A scalar is how big something is. Physicists generalize the idea by using either a real or a complex number. Which one gets used depends on the situation.
[clarification: one can get a bit fancier and define a basis vector for a scalar, call it e₀. It is only in physics graduate school that one entertains values of e₀ other than one. This basis vector only has dimension, but does not have direction. By that I mean nothing happens to its value in a mirror.]
A vector has both a magnitude and a direction. Vectors are pointy. Here one first learns how nuanced definitions can be in mathematics. There is no one right way to point. Instead one provides a basis vector to do the work of pointing. A vector in n dimensions can be defined like so:

$V = v_1 e_1 + v_2 e_2 + … v_n e_n$

Take a scalar, big or small, real or complex, and multiply it with the vector to make a new vector, resized. [note: added e₀'s]

$s V = s v_1 e_0e_1 + s v_2 e_0e_2 + … s v_n e_0e_n$

Two scalars can be added together to make a new scalar. Two vectors with the same set of basis vectors can be added together to make a new vector.

The dot product takes two vectors with the same basis vectors and returns a scalar. Technical jargon can be confusing at this point since physicists often speak of scalars as numbers that don't change under a transformation. Instead, I will consistently use the earlier definition: one number with no pointiness.

When introduced to students, the basis vectors invariably have a particular property: the basis vectors are orthonormal. The ortho indicates that the dot product between any two different basis vectors happens to be zero. The normal indicates that the square of any basis vector is unity. The dot product between two vectors V and W is:

$\\ V = v_1 e_1 + v_2 e_2 + … v_n e_n \\ W = w_1 e_1 + w_2 e_2 + … w_n e_n \\ \\ V \cdot W = v_1 w_1 + v_2 w_2 + … v_n w_n$

There was no need to write down e₁² since that evaluates to unity. There is a simple interpretation of the dot product: it represents the cosine of the angle between the two vectors.

The basis vectors span the vector space. All possible vectors in the vector space can be described by a combination of scalars and the orthonormal basis vectors.

The basis vectors need not be orthogonal, nor must they be normal. Changing the basis vectors changes the details of calculating the dot product, making things more complicated. The job is accomplished by using a metric tensor. The elements down the diagonal are for the squared basis vectors. The off-diagonal terms provide rules for the dot product between two different basis vectors. I plan on going into this subject more next week.

The cross product of two vectors generates a third vector. The length of that vector is equal to the area of a parallelogram created by the two vectors. If the vectors point in the same direction, there is no area, and thus the cross product is zero. There is a simple interpretation of the cross product: it represents the sine of the angle between the two vectors. If the angle is zero, then the sine is zero. A sine is an odd function. One manifestation of that property is that reversing the order of the two vectors in a cross product changes the sign.[clarification: if one uses two polar vectors - they are vectors that in a mirror still point the same direction - then the cross product is an axial or pseudo vector, it flips signs. In three dimensions with orthonormal coordinates, the cross product is:

$V \times W = (v_2 w_3 - v_3 w_2) e_1 +(v_3 w_2 - v_2 w_3) e_2 +(v_1 w_2 - v_2 w_1) e_3$

In higher dimensions, the magnitude of the cross product is known from the sine calculation. One set of values for the cross product cannot be pinpointed, so the meaning is more difficult to track down. That subject is beyond the scope of this blog.]

If the cross product is about sines while the dot product is about cosines, there should be a link between the two.

$\begin{align*} | V \times W | &= |V| |W| \sin \theta \\ V \cdot W &= |V| |W| \cos \theta \\ \\ | V \times W |^2 + (V \cdot W)^2 &= |V|^2 |W|^2 (\sin^2 \theta + \cos^2 \theta) \\ \\ | V \times W |^2 &= |V|^2 |W|^2 - (V \cdot W)^2 \end{align*}$

This is Lagrange's identity.

*** Start Historical Interlude ***

Wikipedia appears to give credit for the jargon of vector analysis to Prof. Gibbs of Yale and thermodynamics fame. I recall reading that it was Hamilton who coined the jargon as he dissected quaternion products. Certainly one person came up with the word dot product and the corresponding divergence, as well as the cross product and its calculus clone the curl. I don't spelunk into math history and thus don't have access to primary source documents.

Hamilton had searched in vain for a way to multiply and divide triples of numbers for a decade. The day after his discovery of quaternions, he defined "pure quaternions," those whose first term is zero so that the result is a triple. He abandon the inherent scalar + 3-vector nature of quaternions since it did not fit his expectation. This is a common error, one I am guilty of too.

*** End Historical Interlude ***

Quaternions are all about automorphisms. Start with a quaternion and end with a quaternion no matter what has happened in between. It is like everyone (almost) says: there's no place like spacetime, there's no place like spacetime, there's no place like spacetime. Something starts in spacetime and that's where it ends, be it a big collection of events like a supernova exploding, or an electron absorbing a photon. My life starts in spacetime and that's where it will end. On a small scale, the automorphisms are reversible. Reversibility is a reason I cling to division, multiplication in reverse.

What is multiplication? I learned about multiplication using blocks:

I could count them: 1, 2, 3, 4. [Note: these are the blocks of a real three year old and the block for the number four is misplaced.] The next step was to group them and multiply.

This is the cliché of multiplication: 2x2=4.

There is a different way to line up the boxes so now they make up an area.

Two times two still equals four, but now the repetitive addition applies to a plane.

Go up one more dimension to describe a volume:

I could count all eight, or form three groups of two and form the product: 2x2x2=8.

This is trivial for readers here at Science 2.0. It is the next step that gets fun. How do you go up one more dimension? I cannot do it with blocks...or maybe I can so long as I view the blocks as moving through time as well as space. Repetitive addition in spacetime leads to an object moving at a constant velocity.

It is the appeal of logical consistency that keeps me close to quaternions. If repetitive addition is how I understand multiplication for lines, areas, and volumes, the same should apply in spacetime. I have been able to see lines, areas, and volumes that move with my quaternion animation software working with two, three, and four parameters respectively.

Look at the four vector algebra operations - scalar * scalar, scalar * vector, dot and cross product - from a quaternion product automorphism perspective

$(v, \vec{V}) \times (w, \vec{W}) = (v w - V \cdot W, v \vec{W} + \vec{V} w + \vec{V} \times \vec{W})$

One can pluck out each of these. This is what I expected to see based on my training in vector algebra.

If the quaternion product is viewed as an automorphism - start with two quaternions and end with a quaternion - then any and all operations that are part of a quaternion product must share this quality. If one wants to look only at the dot product, that would be done like so:

$(V - V^*) \times (W - W^*) + ((V - V^*) \times (W - W^*))^* = (-\vec{V} \cdot \vec{W}, \vec{0})$

One could complain about the complexity of this quaternion expression. Yet it is a result of the request to look at only three of the sixteen terms of a quaternion product. Note the zero [quaternion] vector, required so that the result has all the properties of a quaternion.

I can no longer honestly say there is a vector dot product in a quaternion product. A vector dot product as defined earlier in this blog leaves a [quaternion] vector undefined. The quaternion dot product - a distinct beast - requires the quaternion vector with zeros. Undefined is different from zero. Quaternions also constrain the number of dimensions in play. A vector dot product can work in an arbitrary number of dimensions with is not the case for quaternions [which has only four dimensions].

The same holds true for a [quaternion] scalar times a [quaternion] scalar. In vector algebra, the product is the end of the story. With quaternion automorphisms, the quaternion scalar sits besides three zeros, and the product has three zeros so that it too is a quaternion. The quaternion scalar is constrained to be a real number, while the 3-vectors are imaginary.

A [quaternion] scalar times a [quaternion] vector looks like so:

$(v_0 e_0, 0, 0, 0) \times (0, w_1 e_1, w_2 e_2, w_3 e_3) = (0, v_0 w_1 e_0 e_1, v_0 w_2 e_0 e_2, v_0 w_3 e_0 e_3)$

In vector algebra, there is no notion about keeping a place at the table for a [quaternion] scalar. With quaternion automorphisms, the spot is saved automatically.

A [quaternion] vector cross product is all about [quaternion] vectors. With quaternions, the silent scalar has a role. [Clarification: if one has "normal" polar vectors as the quaternion vector, then the cross product is an axial quaternion vector. This is a happy accident of 3D quaternion vectors, and the issue of a cross product in more or less dimensions is beyond the scope of this blog.]

The elephant that lives in my room are the relationships between these various parts. With quaternions the relationships are fixed so that one can multiply and divide them. In vector analysis, it is divide and conquer. Vector analysis has crushed quaternions, that is the history. I will continue riding the real and imaginary elephant wherever it goes.

One can see the difference between vector algebra and quaternion automorphisms. I chose two quaternion polynomials pretty much at random and formed their product. Here were the polynomials with the parameters (a, b, c, d):

$\\ v_t = a + b + c - d\\ v_x = (a - b + c - d)^3\\ v_y = a + 2 b - c + d\\ v_z = a - b - 3 c + d\\ \\ w_t = a + b + c - d\\ w_x = (a + 2 b - c + d)^2\\ w_y = (a - b + c - d)^3\\ w_z = a - b - 2 c + d$

Both have a cubic term, V with x, W with y. The W polynomial also has a squared term in x. Here is the animation using just the parameter a:

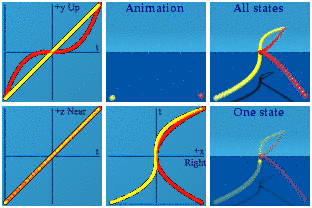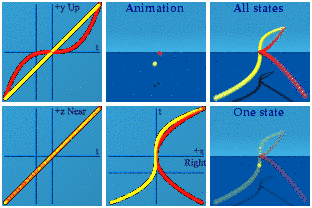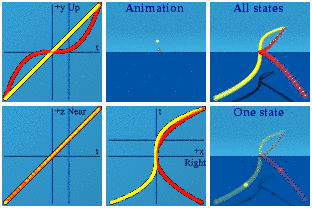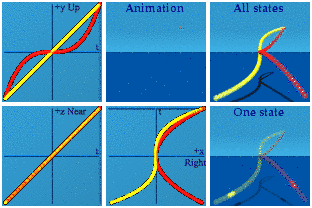
The s-shaped curve indicates a cubic, while the parabola indicates the square. So the yellow is the function V while the red is W. One can now form the product of these two polynomials, color it in green:

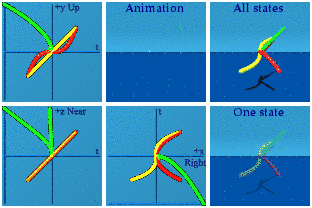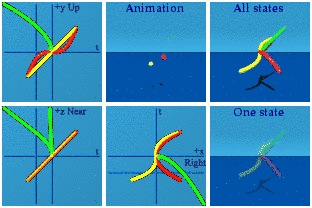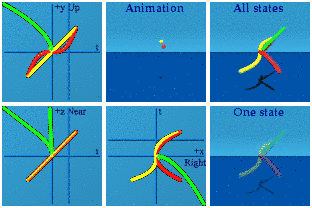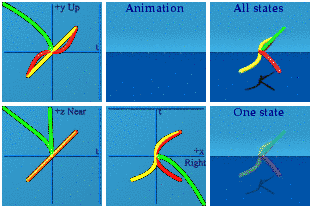
Apparently the first term is always negative for the numbers created by this product.

Here is just the product, in isolation, with the dot product in orange and the cross product in pink.

The dot product sits at the spatial center of the animation, while the cross product blinks on the screen for one frame where t=0.

To save some of the commenters the trouble, this was a random pair of polynomials forming just as random a product. I don't claim this maps to anything physicists study. Hopefully some will recognize the potential power with these initial doodles. Almost any function can be constructed out of a polynomial series, including those that are the subject of study in physics.
[To point out an example, one can study the sine function which can be written as a polynomial expression. The sine function is relevant to the description of numerous physical systems.]

The same darn polynomials can be used with two parameters to create a world of strings.

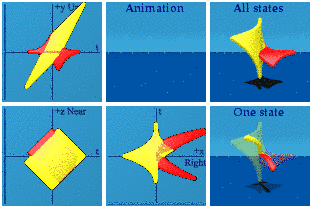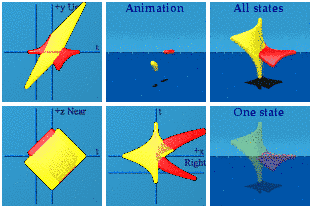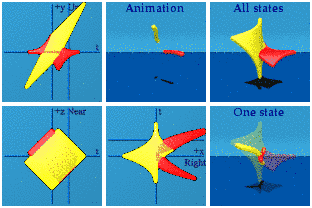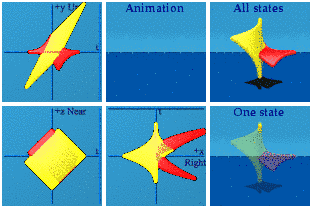
The square and cubic aspects of the polynomials are less clear.

One can still form a product:

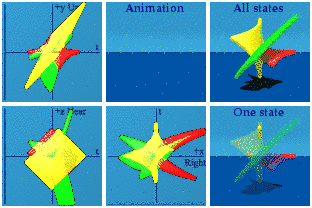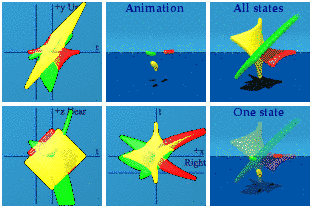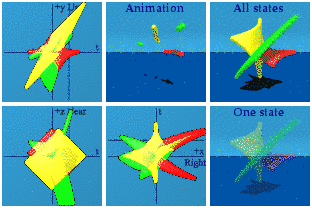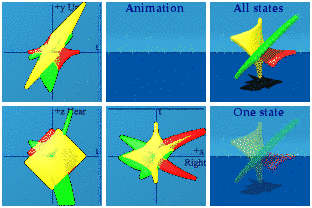
The green string is doing quite a bit more as can be seen when isolated:

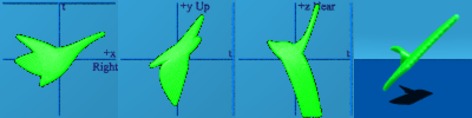
This is vaguely bird-like.

I did spend a few hours generating the three and four parameter animations, which involve membranes and solids, but I don't think they will add to the discussion. There are readers who are vocally against any of these animations. Most readers probably just scratch their heads since the animations don't map to subjects studied in physics or math. This work gives me some hope that all the way brighter folks playing with strings do not represent a complete waste of time and money.

Doug

Snarky Puzzle: I learned if you cross product is zero, then you have nothing but dot product, and visa versa. Is that always true? Worry about the 2 parameter situation...

Next Monday/Tuesday: Scalars, Vectors, and Quaternions: Life Without Orthonormal Basis Vectors (2/2)

[Note: all definitions written in terms of components relied on the explicit assumption that the basis vectors were orthonormal. All that were written with dot products and curls should remain unchanged if the basis vectors are no longer orthonormal. The blog will make an effort to address that issue.]

Comments

If the point of this introduction is to lead into a discussion of 4 dimensions, and our spacetime in particular, then can you please rewrite your introductions to:
1) work for any dimension (or at least 4, as currently you have not defined cross products clearly -- or really at all)
2) don't _define_ a dot product as what you do with the components of a vector in a cartesian coordinate system in Euclidean space (eventually you want to discuss spacetime, which is not Euclidean, and even before that there is the issue that what you wrote doesn't explain what we do for example with a displacement vector written in spherical coordinates)

As David explained, we need to understand the basics before we can go to something more advanced. As currently setup it looks like you are about to introduce the more advanced definitions while introducing some new concepts at the same time and thus clouding everything considerably.

"The dot product takes two vectors with the same basis vectors and returns a scalar. Technical jargon can be confusing at this point since physicists often speak of scalars as numbers that don't change under a transformation."

I'm worried that you aren't understanding what a dot product is if you feel that a distinction needs to be made here. Write out the dot product using tensor notation if it makes it clearer to you. How does the dot product transform as you change coordinate systems? It doesn't change. It is a scalar in "both" senses of the word.

"The cross product of two vectors generates a third vector."

No it does not. The result of a cross product does not transform like a normal vector.
Imagine you are just looking at two dimensions. What is the cross product of two vectors in this space? Is it still a vector "in this space"?

You are recreating a bunch of historical errors, as understanding what the cross product "was" took people a while. If you are going to delve into this subject it would be best to learn from history instead of just recreating their mistakes.

The issue is that in the very special case of three dimenions, this "object" looks kind of like a vector. Requiring this expectation lead to difficulties in finding a generalization. Eventually mathematicians learned the geometric nature of this object. It is related to the wedge product.

from wikipedia:
"The Hodge dual of the wedge product yields an (n−2)-vector, which is a natural generalization of the cross product in any number of dimensions."

Only in the _very_ special case of n=3 does this map to an n=1 object, thereby making it look like an operation that takes a vector and another vector and yields a "vector".

So please get a proper geometric understanding of these objects if you are about to "leap" into interpretting them as geometrical objects in 4 dimensions (and especially the non-Euclidean 4 dimensions of spacetime).

Anonymous (not verified) | 06/05/12 | 10:44 AM

Link

1). work for any dimension

The post focuses on 4 types of operations that happen in scalar and vector algebra which I will subsequently refer to as vector algebra for short. These four definitions of vector algebra can be applied to arbitrary dimensions. It seems to me that is the implication in the clause of the first sentence "defined in the first steps to more than one spatial dimension."

2) don't _define_ a dot product as what you do with the components of a vector in a cartesian coordinate system in Euclidean space (eventually …

There is no eventually, there is what is in this blog. I am going to use the first definition of a dot product I learned:

$V \cdot W = v_1 w_1 + v_2 e_2 + …+ v_n w_n$

The basis vectors do not have to be Cartesian. They must be orthonormal for this definition to work. I have kept this basic.

Nothing in this post was about how anything transforms. That is why these are the basic definitions.

No it does not. The result of a cross product does not transform like a normal vector.

By "normal" vector, I believe you mean a polar vector. The cross product would then be called an axial vector. In this blog, I clearly defined what I meant by the word vector: a magnitude and a direction. One could make my statement more technically precise like so:

"The cross product of two [polar] vectors generates a third [axial] vector."

I consciously decided not to dive into those bits of jargon.

There sure are lots of problems with working in whatever-I-feel-like number of dimensions. I am going to stay planted in one dimension of time, and three for space.

Doug Sweetser | 06/05/12 | 21:23 PM

Link

"These four definitions of vector algebra can be applied to arbitrary dimensions."

I very clearly explained why your idea of a cross product does not work in arbitrary dimensions.
Actually, you didn't even clearly define a cross product in 3 spatial dimensions.
If you really think your idea works in arbitrary dimensions, then learn by translating the following problem into math and working it out:
-- Given your definition of a cross product, what is the cross product of two four-vectors? --

And if you want to " stay planted in one dimension of time, and three for space.", again I must point out that your definition of the dot product is CANNOT BE USED for spacetime. Spacetime is NOT EUCLIDEAN.

You immediately jump to mentioning spacetime with quaternions, but your definitions don't work for spacetime.

Anonymous (not verified) | 06/05/12 | 22:44 PM

Link

I will concede the point: the cross product can only be defined uniquely in 3 (or 7 apparently) spatial dimensions. Lucky for me I work with quaternions that have 3 spatial dimensions.

The time part is not pointy. Time goes into the [quaternion] scalar times a [quaternion] scalar calculation. Quaternions are all about relationships. The norm of a spacetime quaternion, q* q, is the sum of a the [quaternion] scalar times a [quaternion] scalar plus the 3-vector dot product of the [quaternion vector] parts. The square of a quaternion, q², is the difference of a [quaternion] scalar times a [quaternion] scalar minus the [quaternion] vector dot product of the spatial parts.

[math for clarification:
$\\ q^* q = (t, -\vec{R}/c) \times (t, \vec{R}/c) = (t^2 + \vec{R}\cdot\vec{R}/c^2,\vec{0})\\ \\ q^2 = (t, \vec{R}/c) \times (t, \vec{R}/c) = (t^2 - \vec{R}\cdot\vec{R}/c^2,2 t \vec{R}/c)\\$

Doug Sweetser | 06/07/12 | 19:05 PM

Link

"I will concede the point: the cross product can only be defined uniquely in 3 (or 7 apparently) spatial dimensions."

The point is that you are not understanding geometrically what a cross product is. It is not really a vector; you are taking a coincidence and trying to abuse it. Don't stick you head in the sand; if you want to play with these objects learn what mathematicians have figured out about these objects long ago. If you stick with 3-dimensional objects, it is possible to plod forward with the cross product 'vector' analogy. But If you want to discuss spacetime, which you clearly do since you keep relating quaternions to spacetime, you need to take the time to learn what these objects are.

The geometric generalization of the cross product is defined just fine in 4 dimensions. It is just even more clear in that case that it is not a vector.

"The time part is not pointy."

Let's first discuss four-vectors. As a vector object is it not just the "spatial" components that are "pointy". You have four basis, each "pointing" in a direction in spacetime. Each component gives an amount in that direction. The entire thing is a vector, not just the "spatial" part.

Similarly if you want to consider the mathematical "space" of quaternions, and choose a basis so you can represent them with four components, you have a four-dimensional vector space. Due to the nature of quaternions, in addition to an addition operation, you also have a multiplication operation, which is an interesting additional structure for a vector space. That additional interesting structure doesn't somehow magically change the dimension of the vector space. You CANNOT declare only a subset of the vector components as "pointing" in this space. The entire thing, the whole object, is a vector in a four dimensional space.

"Lucky for me I work with quaternions that have 3 spatial dimensions."

Your quaternion space is 4 dimensional. By the usual definition of the norm in this space, It is also Euclidean. So this maps just fine to a 4 dimensional Euclidean space. Why are you declaring a quaternion to be only 3-dimensional? And why are you declaring the remaining component to be non-"pointy"? Since it is Euclidean, why don't you consider all four dimensions "spatial"?

As David explained, you should take the time to clearly define your foundations. Instead you have taken huge leaps and bounds backwards.

Usually you finally make progress after David comments or repeats what others have said. So I am surprised at the pushback here for something David has already said. Maybe if we're lucky David will stop by and gently push again for clearly defining your foundations. You currently have a really jumbled view of all these objects, and it is crucial to congeal the foundations before attempting to build up.

Anonymous (not verified) | 06/06/12 | 14:32 PM

Link

The subject of the blog was accurate: it was about the definition of scalars and vectors, and the first four operations we use. As such, I did modify the main blog to note there is a basis vector that pals around with a scalar even though it rarely gets assigned a value other than unity. I also added in the cross product definition for a 3D spatial vector. The discussion of a cross product in more than three spatial dimensions is beyond the scope of the blog.

I am going to stick with the cross product that appears as part of a quaternion product. Feel free to pontificate about all the things you know about cross products, but the subject is beyond the scope of this blog.

A quaternion does have four basis vectors. That does not mean the qualities of the four basis vectors are the same. One of the basis vectors only has a magnitude. The other three have a magnitude and a direction. In the quaternion product, it is only those element that have a basis vector that has the magnitude and a direction that are part of the cross product. The cross product in a quaternion uses 3 out of the 4 parts of a quaternion.

Doug Sweetser | 06/06/12 | 20:47 PM

Link

Doug,
Based on David's comments and your reactions to other posters, I think we were all expecting you to clearly define your foundations here. Your title "Scalars, Vectors, and Quaternions: Definitions" seems to suggest this as well, but the article only brings up more questions about your take on these objects than it gives answers.

You immediately jump into considering a quaternion as a scalar and a vector, but you don't clearly define the relation you are assuming between these.

Your understanding of dot-products is confusing, based these statements:
1) "The dot product takes two vectors with the same basis vectors and returns a scalar. Technical jargon can be confusing at this point since physicists often speak of scalars as numbers that don't change under a transformation."
and
2) "A vector dot product as defined earlier in this blog leaves a 3-vector undefined."

Does this mean you are trying to use quaternions to 'extend' the definition of a dot-product as a way to take two vectors and get another vector?

And as for the cross product, you never really define that.
Based on the above info from Anony it looks like there is a lot more there that needs to be dug into. (I'm curious based on his comments ... is a "cross-product" in 2 dimensions give an d=n-2=0 object; a pseudo-scalar somehow related to the sine of the angle between the vectors?)

You also make comments suggesting (as before) that you are equating quaternions with four-vectors on our spacetime, but you don't say how, and then instead of treating them like a vector with four-components you immediately treat it and discuss it like a scalar and a three-vector. So what is it? And precisely what is the relation? Are you "equating" the basis vectors of quaternions with those of the four-vectors as others have suggested?

If you meant to clearly define to us how you are relating quaternions to these things, you have only succeeded in confusing at least this one reader. If anything, it feels like we have gone backwards, since before this I would have sworn everyone was on agreement of what a dot-product was. Now I'm not even sure about that.

Instead of moving on, would you consider rewriting this article next week?
Having a foundation we can all build on for discussion is crucial.

CuriousReader (not verified) | 06/05/12 | 11:13 AM

Link

Here are the four vector operations under discussion:

1). A scalar times a scalar

$s \times t = s t$

2). A scalar times a vector

$s \times V = s v_1 e_1 + s v_2 e_2 + … + s v_n e_n$

3). Dot product of 2 vectors assuming orthonormal coordinates:

$\begin{align*} V \cdot W &= |V| |W| \cos \alpha \\ &= v_1 w_1 e_1^2 + v_2 w_2 e_2^2 + … + v_n w_n e_n^2 \end{align*}$

4). The cross product of 2 vectors

$V \times W &= |V| |W| \sin \alpha$

I chose this definition because it is easy to imagine working for an arbitrary number of dimensions. To make up for my omission, I do so presuming orthonormal coordinates in 3 spatial dimensions:

$V \times W &= (v_2 w_3 - v_3 w_2) e_1 + (v_3 w_1 - v_1 w_3) e_2 + (v_1 w_2 - v_2 w_1) e_3$

These should be simple enough to understand in an arbitrary number of dimensions.

[Oops...This definition only works to define a unique result in 3 (and in a way I don't get yet 7) spatial dimensions. The cross product is perpendicular to the input V and W. That along with the magnitude is three constraints. For something with 4 spatial components, there are three constraints and four unknowns. One could work with the entire set of cross products or pluck one out in some way. That is the world of exterior algebras).

Quaternions don't have such freedom. No one is discussing the core point I repeated over and over: quaternion products are automorphisms, once a quaternion, always a quaternion. This is how those four operations look like for quaternions:

q1). Quaternion scalar times a quaternion scalar

$(s, \vec{0}) \times (t, \vec{0}) = (s t, \vec{0})$

q2). Quaternion scalar times a quaternion 3-vector

$(s, \vec{0}) \times (0, \vec{V}) = (0, s v_1 e_1, s v_2 e_2, s v_n e_3)$

q3). Dot product of 2 quaternion 3-vectors assuming orthonormal coordinates:

$\begin{align*} ((V \times W) + (V \times W)^*)/2 &= (-|(V| |W| \cos \alpha, \vec{0}) \\ &= (v_1 w_1 e_1^2 + v_2 w_2 e_2^2 + v_3 w_3 e_3^2, \vec{0}) \end{align*}$

q4). Cross product of 2 quaternion in orthonormal coordinates

$(V \times W + W \times V)/2 &= (0,v_2 w_3 - v_3 w_2) e_1, (v_3 w_1 - v_1 w_3) e_2, (v_1 w_2 - v_2 w_1) e_3)$

q1) is not 1), q2) is no 2), q3) is not 3), q4) is not 4). Quaternions put constraints on the relationships between q1-q4 that are not there in vector algebra.

That is as much of a rewrite as I will do, sorry.

Doug Sweetser | 06/06/12 | 07:40 AM

Link

"The cross product of 2 vectors
V x W = |V| |W| sin a
I chose this definition because it is easy to imagine working for an arbitrary number of dimensions."

Doug, that is not a definition. That only defines a magnitude.
As you correctly wrote in your article, all that gives is:
|V x W| = |V| |W| sin a

And in all of these operations you have not defined how to obtain the magnitude. Which is especially important since you define the dot product in terms of this.

"To make up for my omission, I do so presuming orthonormal coordinates in 3 spatial dimensions:
V x W = (v2 w3 - w2 v3)e1 + (v3 w1 - v1 w3)e2 + (v1 w2 - v2 w1)e3
These should be simple enough to understand in an arbitrary number of dimensions."

I don't understand this leap. Or at least for me it is not "simple enough to understand" how to expand that to an arbitrary number of dimensionss. Consider for example, as Anonymous brought up earlier, how would you generalize that to two dimensions?
(v1,v2) x (w1,w2) = ( ? , ? )

Or even better, since you want to jump to 4-d spacetime, what is the cross product of two four-vectors?
Or even what is the cross product of two vectors in a 10 dimensional Euclidean space?

"That is as much of a rewrite as I will do, sorry."

Please don't give up so quickly.

CuriousReader (not verified) | 06/06/12 | 00:34 AM

Link

"And in all of these operations you have not defined how to obtain the magnitude. "

Rereading, that sounded strange after the previous statment. To be clear you defined the magnitude of the cross product. What I mean is that you didn't define how to calculate
|A| for a vector,
even though you use this operation in multiple parts. (especially where you use |V| of a quaternion V)

This is particularly important when making the leap to 4-d spacetime like you do.

CuriousReader (not verified) | 06/06/12 | 00:44 AM

Link

Sorry, my statement about higher dimensions was too strong. The magnitude of an exterior product can be defined precisely. What gets lost is more than 3 dimensions is determining a unique direction for the 3-vector.

The constrains that fix things in 3 spatial dimensions are the magnitude, and the fact that the dot product of the cross product with the input 3-vectors must both be zero. Three equations, three unknowns. In four spatial dimensions, there are the same three equations, but now four unknowns. As such, there is now an infinite but restricted set of four vectors that meet the conditions of a cross product.

In one draft, I had written about the cross product being constrained to operate in 3 spatial dimensions (and it can also work apparently in 7 spatial dimensions, but I have not figure that one out at this time). I figured the Anonymous would bitch about exterior algebra if I did that. What is funny is that the complaint that the cross product can only work in a robust way with 3 spatial dimensions (unlike the dot product or scalar times a vector) strengthens my proposal to use quaternions.

I don't care about defining a cross product in two, four or ten spatial dimensions where all I really can pin down is the magnitude, not the direction. I stick with three spatial dimensions where I get both magnitude and direction.

Doug Sweetser | 06/06/12 | 07:36 AM

Link

We seem to be talking past each other.

I see you updated the article, but in a way that seems to betray more misunderstanding.
This is very frustrating, to think that we can't convey such simple concepts using English and math.

I see you are now qualifying a lot of your statements by specifically saying "spatial" dimensions. Are you trying to say something with that? Do you really consider a four-vector as just a time piece with no direction and a 3-vector in space? Where is this coming from?

"What is funny is that the complaint that the cross product can only work in a robust way with 3 spatial dimensions (unlike the dot product or scalar times a vector) strengthens my proposal to use quaternions."

NO! Why do you call three of the components of a quaternion a dimension, but not the last one?
If you are going to write quaternions in a representation with four component objects, the vector space of quaternions is four dimensional, NOT three dimensional as you keep claiming.

This is crazy bizarre, since you used to insist on equating quaternions with four-vectors, now you seem to insist that one component has no "pointedness" and quaternions are just a three-dimensional object. What in the world is going on?

"I stick with three spatial dimensions where I get both magnitude and direction."

Are you giving up on 4-dimensions completely then? Are you now saying quaternions can't relate to four-vectors because they have a different dimension?

I am so very lost. What in the world are you saying?

I think it would help if we can at least agree on what a vector space is first. Read David's article on this site which gives an introduction to vector spaces, and tell me if we can agree on that definition (except, for obvious reasons, requiring positive definiteness of |V|^2 for a vector V).

CuriousReader (not verified) | 06/07/12 | 02:18 AM

Link

Doug:

You lament that "No one is discussing the core point I repeated over and over: quaternion products are automorphisms, once a quaternion, always a quaternion."

While I cannot speak for anyone but myself, I suspect that those who know what that "jargony" term ("automorphism") means have chosen to overlook your misuse of that term, as I have.

David

David Halliday | 06/14/12 | 20:25 PM

Link

From wikipedia:

In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.

I was looking at this operation as an isomorphism:

$QScalar[V] \equiv (V + V^*)/2 = (v_0, 0, 0, 0)$

To my eye - at least for now - I think both V and QScalar[V] are full-fledged quaternions, and can be represented by the finite group Q₈ over the field of real numbers. One could point out that QScalar[V] will commute with every other quaternion, and thus is different from an arbitrary quaternion which will usually not commute with another. If that is the reason using "automorphism" is in error, is there a technically more accurate way to describe a function that starts and ends with a quaternion? That is the word I was hoping to find.

Doug Sweetser | 06/14/12 | 20:51 PM

Link

Doug:

While you quoted the right thing from Wikipedia, you didn't check on the definition of "isomorphism".

Your QScalar[V] is not an isomorphism.

David

David Halliday | 06/14/12 | 21:10 PM

Link

"To save some of the commenters the trouble, this was a random pair of polynomials forming just as random a product."

Thank you.

"I don't claim this maps to anything physicists study. Hopefully some will recognize the potential power with these initial doodles."

You just said they were random.
You just said it doesn't map to anything physicists study.
Then you immediately admit you feel there is "potential power with these initial doodles"? This is why people complain. You have a severe disconnect in logic regarding some of your ideas.

I and apparently others were all hoping you were going to concretely specify how you were relating quaternions to vectors in spacetime. Instead we get more of your animations that convey nothing useful to the subject. Color me disappointed.

I echo the previous requests, can you please try again?
Take a week or several weeks if you need to. What ultimately matters is the content, not the self-imposed weekly structure.

-------------------------
To the Anonymous poster(s):
Based on content, it sounds like there are multiple of you. Can you please just use a pseudo-name. I realize if an important point is made that it shouldn't matter who said it, but it makes the discussion hard since I can't tell what previous discussion needs to be repeated, and what level of background each person has.

Anyway, whichever Anonymous did it, I enjoyed the neat post detailing the possible ways to equate the basis of quaternions and four-vectors representations. That alone would make for an interesting article. It seems to directly follows from David's comments, and should be useful when Doug gets to that material.

LagrangiansForBreakfast (not verified) | 06/05/12 | 16:15 PM

Link

"the animations don't map to subjects studied in physics or math. This work gives me some hope that all the way brighter folks playing with strings do not represent a complete waste of time and money."

Can you please fill in the gaps for us?
How do you go from something that you admit doesn't map to subjects studied in physics or math, to then concluding this gives you some hope for string theory?

I'm also having trouble understanding how quaternions fit into any of this.
Based on your definition of cross products for two vectors, what is the cross product for a quaternion? As you mentioned many times, multiplication takes two quaternions and results in a quaternion, and this is one of your defined properties of a cross product. But how do we determine the angle between two quaternions do check if this meets your other requirements for a cross product?

I have no idea where your attempts to define end and your speculation starts. I have no idea what you are concluding.
::very confused::

"This is vaguely bird-like. "

Are you for real?
Gosh, I have no idea why people have complained these animations are not useful.
Good thing you didn't show the 3 or 4 parameter animations because you "don't think they will add to the discussion".
::rolls eyes::

PancakePurpleShoe (not verified) | 06/05/12 | 20:57 PM

Link

The stuff about strings is speculation.

In the popular presentation of work on strings, they say the most fundamental thing in nature is a string. Or at least they said that until there was a membrane that unified the five previously separate string theories. All of that work was happening in 10 or 11 or 26 dimensions. My good friend Bob Weinberg is actually playing around with doing stringy things in 4D. That is where a pro like him might find something, that is my speculation. It is trivial for me to write down animations of strings colliding with string, membranes with membranes, membranes with strings, membranes with of a dynamic solid. Often that needs a trillion quaternions, but I cannot render it. It feels like a bewildering number of possibilities, a problem at some level for work with work on strings.

On quaternions: All the terms of vector analysis were viewed as parts of quaternion products or from doing calculus with quaternions. The terms that go into a quaternion cross product are the same as the standard cross product. One thing I was taught not to do was to add a polar with an axial vector. That is what happens every time in a quaternion product. In essence, that is what I am struggling with, the dichotomy of what I learned from vector analysis and what is in a quaternion product. This has a chance to be a place where dividing the quaternion product into separate parts might block progress.

If these animations represent a new path in the future to understanding physics, your mockery is a good sign.

Doug Sweetser | 06/05/12 | 22:43 PM

Link

I was expecting more. Have you read this? Even if you've already seen this material, it is nice to have it all in one place like this.

Barry Barrett | 06/06/12 | 10:03 AM

Link

That was fun to re-read. In the abstract, he said he was going to connect to the Lorentz group. Once I read that, I go biquaternion hunting, which is what he eventually does but that detail does not make it in the abstract.

He gave Gibbs the credit for pure quaternions which I am confident Hamilton developed on day 2 of his discovery. He defined what he means by the scalar and the vector part of a quaternion (I am writing as a 4-tuple instead of a sum):
$\\ q=(q_0, q_1, q_2, q_3) \\ \\ S q = q_0 \\ V q = (q_1, q_2, q_3)$

The change that happened for me due to this blog is like so:

$\\ q=(q_0, q_1, q_2, q_3) \\ \\ S q = (q_0,0,0,0) \\ V q = (0, q_1, q_2, q_3)$

Partly that is driven by software: the program knows how to deal with 4 numbers separated by spaces. Anything of that form can be animated. Anything not of that form trips up the program.

4.1 Crystallography Someday I will have to play with the crystallography groups. That should be fun.

4.2 Kinematics o rigid body motion. I had quite a bit of fun rewriting Newtonian laws with quaternions. The sure sign of a classical law are lots of zeros in the quaternion generator. I figured out Newton's law in polar coordinates for a central force as a quaternion one-liner. People won't believe it unless they do it themselves.

5. The Lorentz group. He should have given credit to Conway in 1911 and Silberstein in 1912 for the biquaternion trick. I have a pdf of the Silberstein paper on my web site. My guess is that he came to the subject through the minquat door and did not search for the work done with biquaternions which happened to have been done earlier. He did cite those two authors later, so it was just an oversight. The technical thing that worries me is that complex-valued quaternions do not necessarily have an inverse. As such, I don't see how that can qualify as a group since having an inverse is one of the key defining properties of a group. One might try to say one uses complex-valued quaternions whose norm is not zero, but I had a long give and take with David that convinced me that was not a legal constraint to say you still have a group.

I really have issues with the first footnote. There is i, j, k in bold, and i not in bold that is like the other i except it commutes with the others.

6. The general theory of relativity (GTR) group. I don't know if I can believe that section :-) He gets to "the equation of motion of the general theory of relativity" pretty darn fast.

On a social note, it is interesting to contrast the comments on this blog with the exchanges on stackexchange. Two key differences are requiring people to log in (and thus have access to LaTeX formatting tools), and the competition to write the best answer. I am sure there must have been questions there about the cross product in more than 3 dimensions. I know my limitations, and I would not be able to write the "best" answer for that situation. It was great to see people come back and edit their replies about the real-valued quaternion Lorentz "thingie". They did struggle with the standard issues (why not just use complex-valued quaternions?), but the discussion did stay quite focused on the technical issues.

Doug Sweetser | 06/06/12 | 22:03 PM

Link

The technical thing that worries me is that complex-valued quaternions do not necessarily have an inverse.

Are you sure about that? See "Further... is easily verified. This allows an inverse to be defined as follows:" under Algebraic Properties. There is an "iff" qualification gg*=/=0, but it is satisfied by the Lorentz Transformation condition that gg*=1.

One might try to say one uses complex-valued quaternions whose norm is not zero, but I had a long give and take with David that convinced me that was not a legal constraint to say you still have a group.

It depends on what you're trying to do I guess. The quaternions representing Lorentz Transformations will neccesarily have an inverse.
I am very interested in that part on General Relativity. That has to be the shortest derivation of the geodesic equations of motion I've ever seen. But, then again, it "corresponds" to the equation of motion of GR, whatever that means.

Is your formulation of Newton's Laws equivalent to Girards("The quantity in the first square brackets corres- ponds to the acceleration of a fixed point of the rigid body; the second term corresponds to the Coriolis acceleration, and the last term to the rela- tive acceleration. It seems difficult to conceive a simpler derivation of this useful relation. ")?

it is interesting to contrast the comments on this blog with the exchanges on stackexchange

The criticism on stackexchange is constructive. If only this site had an math editor like that. It took me about two hours to write out the mathematics I wanted to talk about in my latest post- and I gave up in frustration. That could be seen as a benefit by some- the general rule of thumb being to avoid mathematics at all costs, but my blog is aimed at people with some minimal knowledge of math (or at least not an outright fear of it).
Speaking of "what you're trying to do." I've lost sight of what your goal is. I thought you were interested in relating quaternions to 4-vectors. Maybe this blog is a step in that direction. It seems as though the relation to 4-vectors is obvious in your "Lorentz Boosts with Quaternions" so I'm not sure what the issue is or where you are going with this. The relation between quaternions and vectors in R^3 is old news. Are you looking for something new there? But, again, this confusion arises because I don't know what your ultimate goal is. Also, could you distinguish your ideas from established known results. As someone else said, sometimes it is unclear where your ideas begin and established results end.

Barry Barrett | 06/07/12 | 06:52 AM

Link

An issue like this came up when I hoped for while that one could use the Klein 4-group and form a division algebra by excluding only those where k* k =/= 0, and k is not zero. That is a kill because anybody who is part of the group cannot have an additional selection criteria. This is why biquaternions are not a division algebra, there are non-zero elements g where g* g = 0. I am not strong enough technically to know if this means an insurmountable problem exists for a biquaternion representation of the Lorentz group.

I called it, "Newton's Second Law in a non-inertial, rotating reference frame". The calculation is straightforward. I have not solved a single problem with it, and try to stay away from those fictitious forces that confuse me so.

As far as the goal is concerned, I have two issues. In vector algebra, people use Jacobian matrices as part of a description of what it means to transform coordinate systems. A metric tensor is needed to take two 4-vectors and form a Lorentz invariant scalar. Neither a Jabobian nor a metric tensor is a quaternion. My open question is if I can find expressions to do those jobs that are quaternions. If all choices of basis vectors were orthonormal, the job of a metric tensor would be far easier to do. I have an idea I will give a try.

Doug Sweetser | 06/07/12 | 21:03 PM

Link

My open question is if I can find expressions to do those jobs that are quaternions. If all choices of basis vectors were orthonormal, the job of a metric tensor would be far easier to do. I have an idea I will give a try.

I would begin by practicing transforming from spinors to 4-vectors and from the spinor metric to the 4-vector metric to get a feel for how this is done in a well established case and extrapolate from there. Because spinors are related to quaternions, if you are successful, your quaternion thing will probably be some sort of messy variation on the spinor thing.

I know you've heard this before, but -given that quaternions are known to relate to 4-vectors in this specific way via spniors- isn't it plausible that there isn't a "nice" relationship between quaternions and 4-vectors. We can see a how the are related already- you could mess with spinors to force the quaternions into a more visible relationship, but why? It seems like you're looking for something that probably isn't there. Physicists and mathematicians have asked the question you are posing, and they've found an answer that involves complex numbers, but why shouldn't it involve complex numbers? Why do you find that more unsatisfying than a transformation with no complex numbers?

Barry Barrett | 06/08/12 | 07:28 AM

Link

One of the ways I describe a quaternion is as three complex numbers that share the same real number. Quaternions necessarily contain complex numbers internally, they have not been banished. The three complex numbers do not commute with each other. I consider introducing a fourth complex number which is exactly like the other three except that it commutes with the others because it makes the math more compact to be a form of cheating.

There is incredibly little wrong with the mathematical structure of physics which is why people can deal productively with the mountain of data flowing out of the LHC to supercomputer centers around the globe. I think quaternions have been avoided for a number of reasons. Top of the list is the real-valued representation of the Lorentz group. That one flaw is simple enough to never take them seriously. Seriously. Second would be the inconvenience of non-commuting. Life is much easier when multiplication commutes. Yet so many things spin and we know things that spin involve variables that do not commute. Sounds like a natural fit to me.
What is the most important finite division algebra, bar none? The real numbers. What is the second most important finite division algebra, at least as far as physics and engineering? The complex numbers. The next division algebra is freak-show rare, showing up for a bit part in doing spatial rotations and the unitary quaternions as a group sitting in the center of the standard model. The three associative finite divisions algebras sound out of balance: GARGANTUAN, HUGE, and trivial.

Doug Sweetser | 06/09/12 | 09:03 AM

Link

I am incredibly confused. You seem to still be claiming a quaternion can represent something relating to spacetime. But in your responses above you no longer seem to consider a quaternion as related to a four dimenional vector, you seem to be saying instead that a quaternions is just a three-vector and a scalar attached.

For example in your response to the cross product issue you seem okay that it doesn't work in four dimensions, because you are not interested in four dimensions, you are only interested in three spatial dimensions!? So are you interested in the four dimensions of spacetime or not?

so very very confused

TimothyMerks (not verified) | 06/06/12 | 13:48 PM

Link

What do you think spacetime is in terms of the basic definitions of scalars and vectors you first learned? I cannot point at time, but I can point three directions in space. So write an event in spacetime like so:
$t e_0 + a e_1 + b e_2 + c e_3$

The e₀-e₄ are the basis vectors. They all have a magnitude. In introductory settings, those are always equal to one. They do not have to be equal to one. The three e₁, e₂, and e₃ have an additional property of direction.

Using the rules of quaternion products, only the a, b, and c are involved in a cross product. Hope that clarifies things a little.

Doug Sweetser | 06/06/12 | 21:15 PM

Link

"I cannot point at time, but I can point three directions in space."

"The three e1, e2, and e3 have an additional property of direction."

You don't seem to understand what a vector is.

A four-vector is a vector in spacetime. Not a vector in space, and a time paramenter. It is a 4-d vector in spacetime.

Consider in some inerital coordinate system an orange is just sitting at the spatial origin. Also there is an apple moving relative to the orange along the positive x axis. What is the four-vector velocity of these two objects? The four-vector is a direction in 4D SPACETIME, not just a direction in some spatial slice of spacetime.

You are disagreeing with the very definition of a vector, which is why there seems to be a huge disconnect with posters trying to reach you on this. How can anyone reach you on this if you deny the very mathematical definition at the starting point? Anonymous's attempt was mathematical, but since you are a visual learner, let me try a visual exercise. Let's imagine a plane in spacetime, parameterized by the coordinates t and x. It's a nice simple plane, so it is easy to visualize.

You say a vector has a magnitude and a direction. Consider the vectors:
(1,1,0,0) and (-1,1,0,0)
Imagine them pointing on our little plane in spacetime. See how they point in different directions?
If not, then let's continue.
They have the same magnitude. What is their direction? Since you claim the time component somehow isn't part of the direction, are you claiming they have the same direction? If not, then you must be starting to see the time component must be part of the four-vector direction. However if you still claim the time component doesn't matter for direction, and so those have the same direction ... then look now where you ended up: two vectors with the same magnitude AND the same direction, and since these are the two properties that define a vector then according to your definition you are claiming those two vectors are the same. A clear concise contradiction.

In conclusion:
A four-vector is, as the name suggests, an element in a FOUR DIMENSIONAL vector space. It is a four dimensional vector. It is right there in the name. I'm not sure how else to say it. Hopefully the "visual" method helped.

TimothyMerks (not verified) | 06/06/12 | 22:43 PM

Link

Thanks for the concrete example.
The event in spacetime (-1, 1, 0, 0) means that it happens at a time -1, and a location in 3D space of (1, 0, 0). The time -1 is measured with a watch. The position (1, 0, 0) can be measured with rulers.

The event in spacetime (1, 1, 0, 0) means it happens at a time +1, and a location in 3D space of (1, 0, 0). If I was always looking in the direction of (1, 0, 0), then I would see one event at time -1, then two ticks of the clock, I would see another event in precisely the same place in space.

I have modified the title to indicate I am discussing quaternion scalars and quaternion vectors. Together, a quaternion scalar and a quaternion vector make up a complete quaternion. Both need basis vectors, so there are four in all. Yet there are differences. For example, in a mirror, the quaternion scalar is not altered while the quaternion vector flips signs.

Doug Sweetser | 06/07/12 | 21:15 PM

Link

Doug, seriously, what keeps causing these disconnects in logic?

Please pause and take a mental snapshot, so you can try to explain to us later what in the world was preventing you from seeing the problem here. No one understands what is happenning when you go into one of these denial loops. Only you can give us insight.

Heck, even just linguistically you should see there is a problem. You write:
"The e0-e4 are the basis vectors."
You also say:
"A vector has both a magnitude and a direction."
so, if e0 is a basis vector, doesn't that suggest to you that it has "both a magnitude and a direction"?

This keep happenning again and again and again.
Please take a mental snapshot of your current understanding and 'reasoning', so that you can effectively look back later and explain to us what keeps causing this. You really need to break this pattern.

You are a smart guy, I have faith you'll once again eventually have everything "click" and it will seem obvious. But until you take the time to figure out what is causing these repeated logical disconnects, you'll just keep cycling this path.

LagrangiansForBreakfast (not verified) | 06/06/12 | 22:53 PM

Link

so, if e0 is a basis vector, doesn't that suggest to you that it has "both a magnitude and a direction"?

e0 is the basis of a quaternion scalar, which together with the quaternion vector makes up a complete quaternion. The reason for the distinction is that they behave differently. Locations get flipped by mirrors. As a math operation, consider the conjugate of a quaternion:

$(t, x, y, z)^*=(t, -x, -y, -z)$

The terms that have a direction flip signs. That happens for three of the four terms. It is this qualitative difference I am trying to communicate, rather poorly.

Doug Sweetser | 06/07/12 | 21:24 PM

Link

First, a scalar is a zero dimensional object. It is just 'value', not direction. So there is no 'basis' for scalars. I'm not sure why you modified your article to add basis vectors to scalars. That makes no sense.

Second, your statements are not logically connected. Let's look at your "logic".
1] you define "locations get flipped by mirrors"
2] you write the statement (t,x,y,z)* = (t,-x,-y,-z)
3] you conclude "The terms that have a direction flip signs."

These statements are unconnected. There is no real logic there.

Let me try a little modification:
consider the mathematical operation
-(t,x,y,z) = (-t,-x,-y,-z)
The terms that have a direction flip signs.
Therefore all terms have direction.

See I can do it to. Can you see the problem in such disconnected "logic" now?

I have problems in general with you immediately, without clearly defining how, considering a particular representation of quaternions to give you a time t component, and spatial x component, a spatial y component, and a spatial z component. Because you refuse to consider quaternions without this association, or define this association mathematically, you then confuse yourself by making vague analogies based on space and time and then _defining_ things to make everything fit your ill suited analogies.

This is not a valid way to deduce anything.

----

Can we at least agree on this? : For a representation of four-vectors in our spacetime, all four basis have directions in spacetime; it is not a combination of a scalar and 3-vector.

I ask because currently it sounds like you are unwilling to consider anything but the "spatial" bases of a vector as giving a direction in the vector space. To help break you of this impasse, I'll try a visual exercise since that seemed to almost get you there.

Imagine the space of quaternions, and randomly choose a non-zero quaternion Q. You can visualize Q as a point in this space. Now add Q and Q to get a new quaternion. Visualize where this new point is in the space. Add Q again, and repeat. This sequence of locations in the space is making a path. Visually it is showing you the direction, as all these points are just n*Q for the natural numbers n, and so differ only in magnitude. ALL four components of Q determine the direction of that path in quaternion space. Try considering a different quaternion that differs from Q only in what you consider the 'time' component. Visualize the new path this quaternion makes. Are the paths the same? Regardless of how you decide to choose your basis for representing quaternions in this space, all four basis have a direction in this space.

Hopefully that visual exercise helped.

LagrangiansForBreakfast (not verified) | 06/08/12 | 01:06 AM

Link

First, a scalar is a zero dimensional object. It is just 'value', not direction. So there is no 'basis' for scalars. I'm not sure why you modified your article to add basis vectors to scalars. That makes no sense.

I tried to be careful and use the word "quaternion scalar" which just means the first term of a quaternion. A quaternion scalar can be formally mapped to the real numbers. It does sound nuts to say real numbers might have a magnitude that is subject to change.

Imagine two grad students build a machine to measure one second exactly. It is designed so a laser signal can start the count to one second. When it reaches that one second, it rings a bell. They are so pleased with their machine, they don't want to share it with each other, so they work together to make a second one. Being all competitive, when the one second is reached, both machines send out a signal that tells the other machine to not ring its bell. The machines are adjusted so within the noise of the electronics, a signal sent to both machines leads to both machines ringing their bells.

They had toiled away in the basement on these one second timers. Late at night, one of the grad students takes his machine up to the top floor. The building happens to have an elevator shaft that is no longer in use. He puts both one second timers in the shaft so that the start signal can be sent from the midpoint of the shaft to start both timers. His one second timer on the top floor now always loses the race to one second. Having failed, he switches the machines so the the other grad student's machine always loses. Whichever machine is in the basement wins the race.

This is just a retelling of the Pound-Rebka experiment. It involves two aspects of spacetime: time and a direction, call it "up". One machine is more up that the other in the Earth's gravitational field. Its signals are redshifted, so it counts a wee bit slower (were "wee bit" can be precisely calculated based on the difference in height in the non-uniform gravitational field). What has changed? The machines are the same. Both count time to one second. It sounds to me like the magnitude of time is different in the basement from what it is at the top of the building.

Can you see the problem in such disconnected "logic" now?

Not yet, but I will make a good faith effort to do so. While I could use my quaternion animation software to do so, I know you are not a fan of that, so have gone for a static representation of animations. Instead of using (t, x, y, z), I will use (t, North, East, Up). North, East, and Up sound like things that have both magnitude and direction ("it is 5 miles that way", pointing), while to me time sounds like something
something with only a magnitude ("it will happen in 15 minutes, whether you are here or there"). Here is a 2x2x2x2 volume of spacetime represented in 5 frames:

There is only one event A, and it happens at (1, 1, 1, 0). Making up=0 was done to simplify this exercise. What I argued was a conjugate operator was a mirror like operation. Here is the result:

That looks like a mirror reflection to me. The direction of A* is different from A, one points to a different place. You countered with the additive inverse of A, -A:

Good old -A is in a different place from A, and it is also at a different time. There is one final possibility, minus the conjugate of A. This flips what I call the quaternion scalar, the time, but not what I am calling the quaternion vector, the final three slots of a quaternion:

The -A* points in the same direction of A.

I have made animations of A, and of A*, and of -A, and of -A*. The A* and -A animations do change where things are. The -A* changes when things are, but not where they are.

At least for now, I still think when has a magnitude while where has a magnitude and a direction.

Doug Sweetser | 06/09/12 | 08:34 AM

Link

All you did was restate the same thing, but with illustrations. It doesn't change the fact that your statements are logically disconnected. The illustrations give no additional information. Your "logic" still relies on your ad hoc a-priori requirement of what a direction "looks" like to you.

Try your illustrations again, but this time instead of drawing a sequence of graphs for N vs E, draw a sequence of graphs of N vs T. Draw an N vs T graph at E=-2, E=-1, E=0, E=+1, and E=+2. Lo and behold, by your definition, now East isn't a direction, and now Time is!

I'm not sure how to discuss this with you constructively other than giving you more visuals till it hopefully "clicks". It is hard to discuss because you disagree with so many fundamental things, including what even counts as a valid logical deduction. So please do the above visual exercise, and hopefully it will help.

"North, East, and Up sound like things that have both magnitude and direction... while to me time sounds like something something with only a magnitude"

Well, then you need to fix your intuition. Is forward in time the same direction in spacetime as backwards in time?
The vector-space of a four-vector has four dimensions. All four basis vectors give directions in this space.

LagrangiansForBreakfast (not verified) | 06/09/12 | 17:24 PM

Link

It does sound like we are at an impasse, so it goes.

Anyone who has made a flipbook animation knows that the pages that go in the flip book are all about space, the where of where things are. The time aspect of a flip book comes from going from frame to frame to frame. Time goes fast if one flips through the book fast. Time goes slow if one flips through the book slow. Time can go in reverse by doing the book in reverse. A typical flipbook doesn't have any labeled axes.

North, East, and Up have a similar relationship to one another: they are directions. Ask anyone in the street. Only someone with too much technical experience with special relativity would think that there is no observable difference between time and a direction. For that reason, I am not going to follow up on your trivial suggestion of writing at 'T' where there happened to have been an 'E'. Time is different from space in special relativity, and one best be precise about how they are different.

Negative time is known as the past. Positive time is known as the future. Zero is known as now. Magnitudes can be positive or negative. Direction involves things like angles. What is the angle involved with time? It is velocity. All the direction for velocity comes from the spatial part.

Doug Sweetser | 06/10/12 | 22:04 PM

Link

"Anyone who has made a flipbook animation knows that the pages that go in the flip book are all about space, the where of where things are."

How can you not see the logical errors in your horrid analogies?
You are presuming an answer, making an analogy about that, and using it to argue a result. This is horribly false logic.

The most painful part is that we don't even need to talk about time. You are just insisting the 0th component of your four-tuple quaternion representation is called time. However the norm as you have defined it is shows the quaternions are EUCLIDEAN. You have four SPATIAL dimensions, not three space and 1 time dimension.

"Time is different from space in special relativity, and one best be precise about how they are different."

Yes it is best one is PRECISE about it. You are not understanding how it is different, let along being precise about it. That our spacetime is different from a 4 dimensional Euclidean space can be seen by looking at the signature of the metric. However your claims are that four-vectors only have 3 basis with directions in spacetime are purely and truly wrong.

"Direction involves things like angles. What is the angle involved with time? It is velocity. All the direction for velocity comes from the spatial part."

You are clearly thinking in Newtonian absolute time; you think time is just a parameter to specify movement in space. That is fine in Newtonian mechanics, but is wrong in relativistic mechanics. It is becoming clearer and clearer that you don't even understand special relativity.

Regarding your angles with time, what do you think a Lorentz transformation is? It is a coordinate rotation in spacetime. Remember that "rapidity" you wrote about before? That is a measure of that angle.

All four vector basis have a direction. Mathematically it should be obvious, and linguistically it is right there in the name.

DAVID WHERE ARE YOU!

LagrangiansForBreakfast (not verified) | 06/11/12 | 14:06 PM

Link

Here is the proverbial disconnect: a quaternion is not a 4-vector. Quaternions do not use metrics to form products, ever. There is some overlap in that both a quaternion and 4-vector can be added to others of their type and be multiplied by a scalar. Quaternions have considerably more constraints on their options that folks who construct vector spaces. As an example, a 4-vector can have real or complex values in any of its four components. The quaternion scalar is a real number, while the quaternion vector is made of three imaginary numbers (imaginary, not complex numbers).

Doug Sweetser | 06/11/12 | 20:29 PM

Link

Dear David,
You appear to have the strongest mathematical background of all the commenters here (no offense to Henry). I, and quite likely almost everyone else, would be very much appreciative if you help Doug work out and understand the mathematical structures of vector spaces, representations of such and use of basis, and how his quaternion components relate to a vector space, and so on. Basically, I am begging for you to please help Doug get a good mathematical foundation to clearly define a starting point for his quaternion adventures.

It is abundantly clear that many watchers had high hopes for Doug finally trying to define how he is considering quaternions related to spacetime. It is also clear we came away disappointed. You have some kind of special connection with Doug, and I plead to you on behalf of everyone following, please help. You are a great teacher and we will all learn a lot, along with Doug.

Please, from one random person on the internet to another, it would be very much appreciated.

Anonymous (not verified) | 06/06/12 | 14:48 PM

Link

I'm sorry that when this was on my "radar screen" I didn't have the time to come here. Then, through the press of things, this "slipped of" my "radar screen".

Just the other day, this was brought to my attention, and I have been reading through the comments.

Unfortunately, I have yet to read through all the comments. However, I have seen a disturbing pattern in Doug's comments that seem to point to a fundamental misunderstanding about vector spaces.

Doug:

Why do you keep claiming that the quaternion "scalar" doesn't "point" in any "direction"?

Why do you seem to think one needs to have a metric, of any kind, in order to have a vector space?

If a quaternion "scalar" doesn't "point" in any "direction", why are you able to add it to a quaternion "vector" that does "point" in some "direction"?

What structure do you have if you have "vectors" able to be added to "scalars"?

Maybe you need to rethink your assertions. Perhaps thinking about what they would imply for the complex numbers may help.

David

P.S. I'll get back to reading the messages here, as quick as I can.

Unfortunately, Doug has gone on with his second installment, so I'll have to check that out as well.

David Halliday | 06/13/12 | 17:17 PM

Link

Let me do the simple one first: a vector space definitely does not need a metric. If one wants to see overlap between 4-vectors and quaternions, that is when one needs to equip 4-vectors with a metric tensor.

Scalars and vectors share a trait: they both have a magnitude. Scalars and vectors differ because a vector has direction. That then leads to the question of how do you know if you have a direction? Its obvious, right? No, to be more precise it is something we can play with in mirrors. How it plays with a mirror depends on what kind of vector it is.

Everyone draws vectors as little arrows, a fine practice. So a 4-vector is a 4-arrow. Case closed, people go home.

If quaternions only had the addition operator and multiplication by a scalar, then I certainly understand why all the terms in a quaternion are created equal, having both a magnitude and a direction. But quaternions do have another essential operator, namely multiplication. Quaternion addition is exceptionally dull. It is multiplication that breaks up the 4-amigos into what I am calling the quaternion scalar and quaternion vector. And all that flows eventually from the group theory structure, good old Q₈ which has the real numbers as a subgroup, what I call in this context the quaternion scalar.

The quaternion scalar adds to another quaternion scalar, the quaternion vector to another quaternion vector. Together a quaternion scalar and a quaternion vector always make up the complete quaternion. In this context, the term quaternion scalar doesn't say how it transforms, unlike the common use of the word scalar. Perhaps I am being foolish to use the words where they first were applied when dissecting quaternion products.

Doug Sweetser | 06/13/12 | 22:09 PM

Link

Doug:

I can only address a very tiny portion of this, at this time.

You say: "If one wants to see overlap between 4-vectors and quaternions, that is when one needs to equip 4-vectors with a metric tensor." Unfortunately, this is completely untrue.

However, I suspect that what you meant was that "If one wants to see overlap between [a particular] 4-vector [space with a particular inner-product {metric}] and quaternions, that is when one needs to equip 4-vectors with a metric tensor [and to ferret out a metric, of one sort or another, for the quaternions as well]."

This latter statement is true. However, this is not the issue, right now. The issue right now is whether the quaternions is a vector space, and, if so, what the dimensionality of that vector space is. (A related issue is the question of what mathematical field the scalars, of any such vector space, are members of. This is usually a simple question of whether the scalars are Real numbers or Complex numbers—and that will suffice, in this case.)

So, the answer to the present issue can be completely addressed without any need, or even desire for a metric.

David

David Halliday | 06/14/12 | 08:31 AM

Link

A counter question: what do complex numbers look like to you? My guess is it is the complex plane. While I am familiar with that old standby, it is the animation of complex numbers that gives me a clear visual about the fundamental difference between real and imaginary numbers. The reals require memory (the past versus the future) while imaginaries can play with mirrors. I doubt you have drunk my Kool-Aid. There are many here who think those animations are loaded with poisons, but I rather like it since it is one of the few bits of mathematical physics I can share with the wife and child. They also liked the Q₈ cube, and I didn't have to tell them the painful story about the subgroups of the same color story.

Doug Sweetser | 06/13/12 | 22:54 PM

Link

Doug:

I suspected that this might be problematic for you (at least at this stage). That's why I used "perhaps". ;)

OK. There are multiple directions we could go from here to help you "see the light". Let's go even simpler.

Do the Real numbers form a vector space? If so, what is the dimensionality? How does the concept of "direction" manifest itself?

Does the fact that the Real numbers have additional operations (though in a rather degenerate sense) destroy any ability to also be a vector space?

(If you are successful in answering these questions, then we shall go on to the Complex numbers.)

David

David Halliday | 06/14/12 | 19:49 PM

Link

Fair enough.

A vector space is a collection of things that can be added together or multiplied by a scalar. That is something I have been saying for years. The real numbers are therefore a vector space. I could check more than a half dozen properties to confirm that is the case. The is one degree of freedom, so the real number vector space has a dimension of one. The fact that one can also do multiplication and division with real numbers in not relevant.

I am pretty sure I got that collection of answers right. Just one more question to go...

The real numbers can be positive or negative. I am thinking that arises out of thinking of real numbers as the group Z₂ (-1, +1) over the positive real numbers (which are not a mathematical field). The concept of direction I think requires things like the concept of an angle, which is a ratio of two elements in a vector space. Since there is only one element, I don't think I can say it has a direction. I have no issue with saying the real number has a positive or a negative magnitude. Yet I suspect that is not the right answer :-)

Doug Sweetser | 06/14/12 | 20:33 PM

Link

Doug:

You did very well, with all but the question of direction.

As I would have expected you to know, magnitude can only be non-negative.

As with all vector spaces that have a norm (norm spaces), all of the Real numbers except zero (the additive identity of the vector space, by the way) can be decomposed into magnitude and direction. So, what directions do we have with the Real numbers?

Another, equivalent way of looking at it is to ask: What directions are allowed for a one dimensional vector space over the Real numbers?

David

David Halliday | 06/14/12 | 20:50 PM

Link

As I would have expected you to know, magnitude can only be non-negative.

I think I will take a hot soldering iron and write that on my arm to I don't forget it. The real numbers have a binary type of direction, either positive or negative. I can admit I was wrong, the real numbers have a binary sense of direction, plus or minus.

The next move is to the complex plane. The real numbers still have their binary sense of direction as do the imaginary numbers. Two dimensions, two degrees of freedom. This time we can even form ratios of the real to the complex numbers.

Add as many dimensions to the vector space as one wants. Each has a magnitude, the positive number, and if one can spot a negative of that new dimension, then one has magnitude and direction. So far, looking really bad for my team.

Hopefully I am not rushing the discussion, but I have been asserting there is "something" different as indicated by quaternion products. This is where one needs to add more structure to the system than appears with 4-vectors. That is where I see the one versus three split, with the three going into the cross product or a dot product, and the one being its real number self.

Doug Sweetser | 06/14/12 | 21:13 PM

Link

Doug:

You were doing reasonably well, until the last paragraph. :/

So, yes, it appears that you may be "rushing the discussion".

You are quite correct that the Complex numbers form a two dimensional vector space over the mathematical Field of the Real numbers. (They also form a one dimensional vector space over the mathematical Field of the Complex numbers.)

The Complex numbers, like the Quaternions, have additional operations, like conjugation, and not only multiplication by Real numbers (as a vector space over the Reals), but also multiplication of vectors by other vectors.

Does any of this "destroy" the Complex numbers being a two dimensional vector space over the Real numbers?

Does the way the Real part of a Complex number acts differently from the Imaginary part "destroy" any of this?

David

David Halliday | 06/14/12 | 21:29 PM

Link

So the name of the vector space game is that involves statements that can only involve addition of two vectors and the multiplication of the vector by a scalar. As such, quaternions over the field of real numbers are a four dimensional vector space. Stop. End of story.

In past, I know I used to say that quaternions were a four dimensional vector space (over the real numbers, but I usually did not add that qualifier which is required). The discussions here did bring in metrics right at the start. That is an additional structure.

A tangential question...Can I also think about complex numbers as the finite cyclic group Z₄ over the real numbers, and thus a four dimensional vector space?

Doug Sweetser | 06/14/12 | 21:51 PM

Link

"The discussions here did bring in metrics right at the start. That is an additional structure."

Yes that is additional structure, but you don't seem to understand that you already introduced structure that constrains it. You brought up dot-products and norms. When physicists say dot-product they mean inner product. The inner product is a mathematical object that takes two vectors and spits out a real value. This is very much related to the metric which is a mathematical object with takes two vectors and spits out a real value.

If you say the norm of a quaternion (a0,a1,a2,a3) is a0^2 + a1^2 + a2^2 + a3^2, technically you haven't specified an inner-product, but you have no freedom to end up with anything but a Euclidean space if you do.

It also doesn't help that you consistently talk about spacetime in these discussions of quaternions. This leads to conflicting statements on what the structure actually gives you versus what you are expecting from it in your not so clear analogies.

"Can I also think about complex numbers as the finite cyclic group Z4 over the real numbers, and thus a four dimensional vector space?"

No. You already asked this.
If you consider the basis set { [1], [-1], [i], [-i] }, you are saying [1] + [-1] is not the same and the additive identity. So what complex number do you claim (1,1,0,0) corresponds to? What about (2,2,0,0) or (2,-2,0,0)?

LagrangiansForBreakfast (not verified) | 06/15/12 | 00:30 AM

Link

The definition of the additive identity for the representation of complex number over the field of complex numbers is z=-z, [correction for morning math head: z + (-z) = 0]
which makes sense since the vector space is one dimensional. With Z₄ over the field of zero + the positive real numbers*, the additive identity would have to be four dimensional, (a, a, b, b). So both (1, 1, 0, 0) and (2, 2, 0, 0) are the same as the complex number zero, while (2, -2, 0, 0) is the complex number 4.

* I have heard people say that the positive real numbers are not a mathematical field because they lack closure: 4 - 8 is not a positive real number. The symbol "-" is an operator, give two numbers it returns a number. I can define it as I like. The positive real numbers are a totally ordered set, so either a>b, a<b, or a=b. Take greater care in defining the minus operator:

if a>b, (a, b, -) means a-b.
if a<b, (a, b, -) means b-a.
if a=b, a-b is the additive identity

To be logically consistent, I think one should do the same for the plus operator, even if it doesn't alter any results.

If and only if one allows these slightly more complicated definitions of addition and subtraction that require ordering based on the magnitude, then 0+the positive real numbers has closure, an identity, and ever element has an inverse - itself.

Doug Sweetser | 06/15/12 | 10:37 AM

Link

"The definition of the additive identity for the representation of complex number over the field of complex numbers is z=-z"

What?
The definition of the additive identity is the element E such that for any element A,
A + E = A

"So both (1, 1, 0, 0) and (2, 2, 0, 0) are the same as the complex number zero, while (2, -2, 0, 0) is the complex number 4."

And you see no problem in both claiming the reals over Z4 as a four dimensional vector space are complex numbers, but also admitting there is no clear mapping between them?

"I have heard people say that the positive real numbers are not a mathematical field"

How about just looking at the definition of a field:
http://en.wikipedia.org/wiki/Field_(mathematics)
one requirement is:
Existence of additive inverses

What is strange is that you even say later
"and every element has an inverse"
so you half-way already see this. So under the addition operator, what element is the inverse of 8? If you restrict yourself to positive numbers, there is none. Hence the complaint.

Anonymous (not verified) | 06/15/12 | 10:19 AM

Link

Sorry for the morning typo, it has been corrected.
Agreed, every element must have an inverse. The inverse element of 8 is 8 because 8-8=0. It is usually the case that the inverse is a different number, but not in the case here.

The difference may be something like:
(+8) - (+8) = 0
versus
(+8) + (-8) = 0
If the rules of the road are the additive inverse needs to be distinct, then so be it because:
(+8) + (+8) = 16

In the standard approach, there are two ways to get to the additive identity, zero:
(+8) + (-8) = 0
(+8) - (+8) = 0
Essential what I am arguing is that having only the later is OK. Now I could be wrong on that point, but it is what I am trying to suggest.

Doug Sweetser | 06/15/12 | 10:54 AM

Link

Unfortunately, Doug, there is no subtraction binary operator in the definition of a mathematical Field. (There isn't even a negation operator. There is the existence of an additive inverse for every element, and we often use a negative sign prefix as a way of signifying such, but it is not truly an operator in the Field.)

So, I'm sorry, you are unable to define such a "Field".

Nice try. ;}

David

David Halliday | 06/15/12 | 13:22 PM

Link

I thought there were two operators, addition and multiplication, and they were suppose to be pretty darn abstract. They become set once the field is chosen. Over the field of positive definite numbers, I say the positive symbol, "+", always acts on the bigger of two numbers, if a>b, then it is a+b. When one gets to how does this "+" work for this particular set, well, it works just like normal subtraction for the real numbers we are familiar with. Then there will be an identity element 0, 8+2=6 will always be in a group, and every element is its own additive inverse, 8+8=0, using the symbol + as defined above.

There also needs to be a group for multiplication, omitting the additive identity zero. There is a multiplicative identity, 1. Every number has an inverse such as 8 and 1/8. And the group is closed because there are no pesky minus signs that demand the complex numbers.

I hope this is at least an interesting try. It is kind of Orwellian: and the plus will be minus...

Doug Sweetser | 06/15/12 | 22:08 PM

Link

Doug, again your mistakes are on the level of definition. You have become way too dependent on everyone else doing your critical thinking. Please pause and try to ask the critical questions yourself to see if you can eventually get to the point where you can ask useful critical questions to evaluate ideas yourself. In this case, as in many others, not much critical thinking is even required since again ... you are disagreeing on the level of the definitions themselves.

http://en.wikipedia.org/wiki/Field_(mathematics)

So doug, with your "-" operator does:
8 - 4 - 2 = (8 - 4) - 2 = 2
or
8 - 4 - 2 = 8 - (4 - 2) = 6
??

Instead of just learning this tidbit, take the time to ask yourself: What prevented you from realizing this yourself? Is there something you need to learn on this higher level to learn from your mistake? At this point these questions are ultimately more useful in your quest than something that can be trivially looked up in wikipedia.

LagrangiansForBreakfast (not verified) | 06/16/12 | 00:30 AM

Link

The operator is not associative, thanks.

Here is what is driving this investigation. Calculus requires a mathematical field, at least that is what I learned in a class on mathematical analysis. Imagine doing calculus on the the interval between +2 and +3. That should work just fine whether or not there are any negative real numbers.

Doug Sweetser | 06/16/12 | 10:49 AM

Link

Doug:

Think about it. Doesn't calculus involve more than just the domain space? Doesn't it also involve the range space?

Besides, doesn't the derivative involve taking differences (addition where one argument is an additive inverse)?

Besides, the reason calculus requires mathematical Fields is because it relies upon all the features of such, including commutativity, associativity, multiplicative and additive inverses, etc.

If you want to be able to do calculus, you need to make sure you preserve all that calculus requires, not just a few of the pieces you can see that you have, but all of the pieces.

Face it, if you truly want to do innovative things, rather than simply "thrashing about", then you need to do the kind of critical thinking that LagrangiansForBreakfast is referring to—being able to ask yourself truly critical questions, and then pursuing them until you fully answer such, even when you absolutely hate the answers they are leading to.

David

David Halliday | 06/17/12 | 21:14 PM

Link

If one hopes to do truly innovative things, it might must be a little tricky, like not having all of one's usual friends at the table. What was productive about this discussion was that the positive reals with the multiplication operator is fine as a group. It is the addition operator that poses a technical challenge. The Orwellian plus would allow one to take the difference between two functions over the positive reals. What is clearly inconvenient is not being associative. I may in the future look into the price one pays for being non-associative. No doubt that has been explored. Don't worry, I won't call this a field. I need to investigate if one can still do calculus. I am not going to absolutely hate any technical result.

Doug Sweetser | 06/17/12 | 21:52 PM

Link

Doug:

The "even when you absolutely hate the answers they are leading to" phrasing was intended as an extreme case, of course.

It's really all about the intellectual integrity necessary for science and mathematics (especially science, I would say, since I believe it's more difficult to fool knowledgeable people with mathematics). As Feynman put it in his "Cargo Cult Science" lecture: "The first principle is that you must not fool yourself—and you are the easiest person to fool."

A potential measure of how well one is doing, in this area, may be how often errors, whether of commission or omission, are caught by oneself, vs. being caught by others.

David

David Halliday | 06/18/12 | 12:19 PM

Link

By the way, Doug, the following are all misuses (or even abuses) of notation:

$(v_0 e_0, 0, 0, 0) \times (0, w_1 e_1, w_2 e_2, w_3 e_3) = (0, v_0 w_1 e_0 e_1, v_0 w_2 e_0 e_2, v_0 w_3 e_0 e_3)$

$(s, \vec{0}) \times (0, \vec{V}) = (0, s v_1 e_1, s v_2 e_2, s v_n e_3)$

$(V \times W + W \times V)/2 &= (0,v_2 w_3 - v_3 w_2) e_1, (v_3 w_1 - v_1 w_3) e_2, (v_1 w_2 - v_2 w_1) e_3)$
(not even counting the missing left parenthesis in the second "slot")

Ether use an explicit basis, or use the 'tuple notation (that involves an implicit basis). Both together do not make good sense.

David

David Halliday | 06/13/12 | 20:11 PM

Link

Bummer, I did that quite a bit in the follow-up article.

I thought more information was a good thing. I am concerned about leaving things implicit. I can write down a quaternion V, or V², or V⁵, and I would think those would have a different dependence on the basis.

Doug Sweetser | 06/13/12 | 22:43 PM

Link

Doug:

Yes. I noticed that I was too late to keep you from using this misuse of notation in your followup article. :}

Yes. I had advised you, and others, to be explicit, rather than implicit. I'm very glad you have taken that advice to heart, and have been trying to be explicit. However, if one wants to be explicit, then one must be explicit, using a basis in a fully explicit way.

David

David Halliday | 06/14/12 | 08:15 AM

Link

Doug, some not so light relief; I'm not sure if you know your history, but Maxwell used 20 quaternion equations to describe electromagnetism in his original 1865 paper, which was presented orally tothe Royal Society in December of 1864. Maxwell had used a scalar and vector potential as variables in his original equations. Heaviside and Hertz converted these quaternion equations into vector differential
equations. Lorentz later applied a symmetric gauge to convert these into the vector equations in the E- and H-field variables we now call Maxwell’s equations.

Do you think you could give an outline of this quaternion description of Maxwell's equations and its transformation into curls and divs please?

—

Tony Fleming Biophotonics Research Institute tfleming@unifiedphysics.com

Tony Fleming | 06/18/12 | 02:21 AM

Link

Comments

Know Science And Want To Write?

What's Happening

Books By Writers Here

Related Articles on Science 2.0

Comments

Know Science And Want To Write?

What's Happening

Books By Writers Here