What is exciting to me is that I am asking questions and developing answers. I want to emphasize the plural. This is not a one trick pony (quaternions can do 3D rotations and nothing else of interest). Many different topics are being raised and looked at from odd angles. I didn’t have a plan to write these puzzles, but am glad they emerged from the blog writing process. Now back to the questions and their answers.
Click or skip a reading of this blog
May 24 - Argand Plane Crash
The Snarky Puzzle
‘Ever’ only lasts until a counter-example is found. A circle in the complex plane has so much spacetime symmetry: it goes out as it comes in, and there are always two points. Discuss how you can find the origin, where and when it is.The Back Story
Circles are central to physics. We were raised on circles in the Euclidean plane. To animate the familiar requires a cylinder in spacetime. Nothing of interest is happening with time for a static circle.
The best field theory we have is the Maxwell equations. The symmetry that goes hand-in-hand with the conservation of electric charge is the unitary group U(1), complex numbers with a norm of 1. The Lie algebra u(1) needs only one complex number to do the job. Time squared plus space squared equals one, simple as that. Life is linear in time. Squaring time is outside our experience. A computer can deal with squared time easy enough.
The Answer
Here is an animation of a thousand random quaternions plugged into this expression:
randq - i randq i | q_norm
The q-iqi business gives quaternions of the form: (a, b, 0, 0) - a complex number using the first imaginary only.
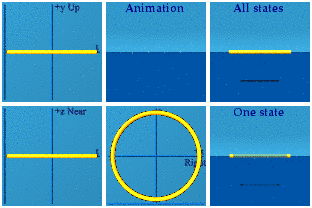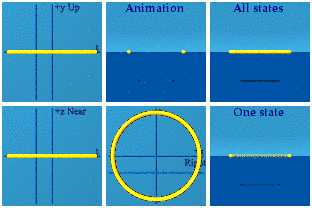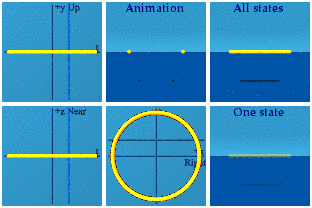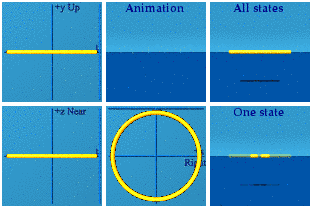
There are two spheres on the screen at all times, a sign of spatial symmetry. The spheres end as the started, a sign of time symmetry. When the two spheres are farthest apart, that marks time = 0, or now. The spatial origin is always halfway between the two spheres. Note how the complex plane circle is a circle only in the Right/Left+time complex plane.
See if this description is valid if the circle is given a Lorentz boost along the x axis.
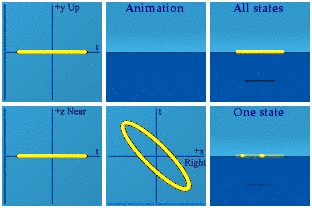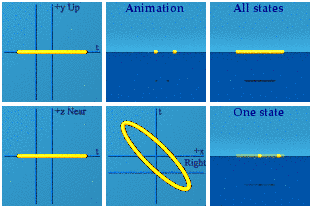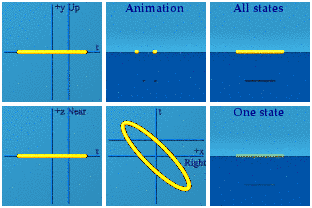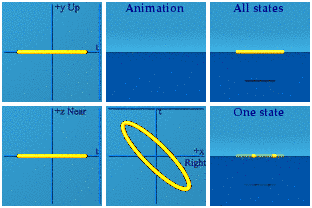
This no longer looks like a circle in the complex plane. One can pinpoint the origin as before: time zero happens when the points are farthest apart, and the spatial origin will be the halfway point at that moment. Spatial symmetry is only preserved if one moves the mirror which would happen with a Lorentz boost. Time symmetry is broken because where the animation ends is not where it begins.
Here is a boost along the y axis:
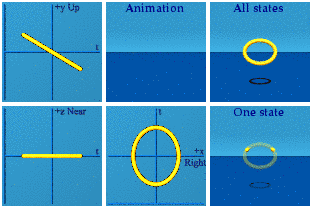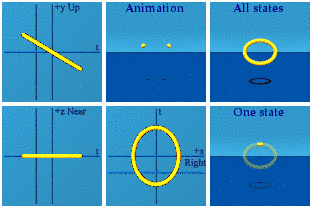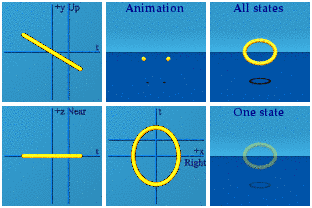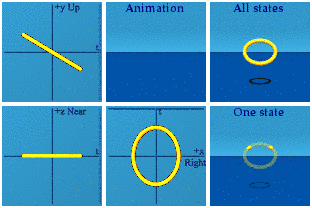
The circle becomes an ellipse because time gets stretched out by the boost. The time symmetry is again broken. The spatial symmetry is preserved.
The Discussion
They say over in wikipedia-land, that a unitary group can be viewed as the intersection of three groups: the orthogonal, the symplectic, and complex groups. This boils down to three statements:
Symplectic: AT J A = J
Complex: A−1 J A = J
Orthogonal: AT = A−1
What they say is if you have two of these, then the third one comes for free. With the quaternion representation, if you have one, you get the other two. Take the symplectic group. Quaternions are a normed division algebra: multiplying the norms of a, b, c separately give you the same as forming the product, then calculating the norm. This means that A must have the norm of one. When the norm is one, the transpose equals the inverse. Fini.
May 30 - Why Quantum Mechanics is Weird
The Snarky Puzzle
Complex analysis is a gold mind of important ideas. Quaternion analysis is a barren moonscape. The best work to date from a guy in the 1930’s was unable to show that q2 is analytic in q, dead end city. Grab a polynomial by the horns. Show that q*2 is analytic in q*. Bonus points if you do your proof five ways.
The Back Story
My first international conference was in Rome in 1999. The second guy to speak - meaning he was important - started to talk about quaternion analysis. He described the problem brilliantly. I was getting so excited. The ability to do quaternion analysis is vital to any robust assault on the accounting system of physics. He started to describe his own approach. It used left-handed derivatives. Yuck. The more he went on, the madder I got. What an odd reaction to a math professor from Oxford. His approach struck me as so terrible, I decided to work on devising a decent quaternion derivative definition.
The Answer
There may be as many as five different ways to show a complex valued function is analytic. I can only recall three ways: the chain rule, the Cauchy-Riemann equations and the holonomic equation [since this is a technical math statement and I work out of an isolation chamber located in my basement, please be gentle if my description here is imprecise]. I am focused on holomorphic functions. These complex valued functions are equal to their Taylor series at every point in their domain.
I am going to skip answering this question. See the discussion below.
The Discussion
The BIG thing that happened due to comments from David Halliday was I realized the norm business was superfluous. What was vital was the multiple limits. David is trying to talk me out of doing those too :-)
David is skeptical of the entire approach. Skepticism is a good thing. He has shaken my confidence on this topic. Please take my work thus far with a large block of salt. In fact, consider it now worth your time worrying about until I come back with another blog on the subject. That blog will have to have an accompanying Mathematica notebook. What I hope to show (and of course might not), is how the single limit definition is broken. Then how using more than one limit works better. If I can get that bit of algebra working, then I would apply it to all the variations in multiple limits. From there I have to travel out to the chain rule, Cauchy-Riemann, and the holonomic equation. Man up.
June 7 - Constructing Consistent Linear Field Equations for Gravity
The Snarky Puzzle
Write out the Maxwell equations in the Lorenz gauge. Write out the hypercomplex gravity equations in the Lorentz gauge (on the last slide). Subtract the first equations from the second. Shop and compare that with the GEM unified gravity and standard model symmetry field equations written in the last slide. Reflect on how important it is to be similar but not quite the same.
The Back Story
As Jan used to say on the Brady Bunch, “Gauge, gauge, gauge, why does gauge get all the attention?” There are entire books on the subject which have yet to make my summer reading list (they tend to be too heavy to lug to the beach). Lagrange densities need to be invariant under a gauge transformation so that particles can zip along at the speed of light. Good for them. But the field equations that result from applying the Euler-Lagrange equations usually depend on the gauge choice. I don’t have a broad enough exposure to know if that “usually” should read “always”.
The Answer
The Maxwell in the Lorenz gauge
The hypercomplex equations in the Lorenz gauge
The GEM unified field equations
The Discussion
I have nibbled on a few pages in Michio Kaku’s “Quantum Field Theory: A Modern Introduction”, a 750+ page book on the subject. One quote stuck with me:
4.3 Quantizing the Maxwell field, p. 106... The problem with this operator is that it is not invertible, and hence we cannot construct a propagator for the theory. In fact, this is typical of any gauge theory, not just Maxwell’s theory. This also occurs in general relativity and in superstring theory.
Does the GEM Lagrangian get around this common plague? The field equations do not change if the Coulomb gauge is chosen, or the Lorenz gauge, or the Feyman gauge, or whatever gauge. This may be a critical difference.
June 14 - Gamma Gamma Girl Graphs
The Snarky Puzzle
Snarky puzzle mystery. Usually I know the answer. This time I don’t. That will make writing the answer harder for me, but I doubt you care. I went way out on a limb to embrace something I have called California numbers. Being from the East Coast, I have trouble doing that. I have a friend who lives out there who is into the barefoot running revival, wearing these “shoes” that have individual places for each toe. In this blog, generated the California number multiplication graph using only quaternions. See if numerically you can show the two are the same: California numbers or quaternion triple products. If this can be done, I can stay on the East Coast with the division algebra quaternions.
The Back Story
I built a clay and pipe cleaner model of quaternions. Except for the little black identity loops, everything is a directional graph: go out with a positive imaginary label from the identity, return with a negative imaginary label. Between two imaginaries, use both signs of the third imaginary.
Everything for the graph of the Klein 4-group uses the same positive label.
The Answer
These two animals are different. The Klein 4-group has 6 edges, and 3 distinct labels. The diagonal gammas have 6 edges and 6 distinct labels because of differences in the signs.
The Discussion
The folks over at math.stackexchange.com are calling this a Cayley graph. Having never studied Cayley graphs, I will let my reader investigate on their own. I do have the Cayley table of the Klein 4-group (what I have always called the multiplication table because I have worked with multiplication since third grade, but have not met Cayley who has long since died).
Here is the Cayley table for the diagonal gamma's graph, substituting 1 for 1q1, 2 for iqi, etc.
The few negatives make a difference.
Doug
Late next Monday/Tuesday: Putting work on the execution line





Comments