The complex plane should be known as the Wessel plane, after the Norwegian-Danish land surveyor. His paper of 1799 was ignored because few were reading the preprint server at that time. Mr. Bookshop in the big city of Paris gets his name associated with graphing complex numbers in a plane. This is one reason I avoid naming things for people as proper credit is complicated.
click or skip a reading of this blog
Let’s look at what the Argand plane gets 100% right. Take an arbitrary complex number z. It has a unique place to call home. Draw its negative, so it jumps the origin:

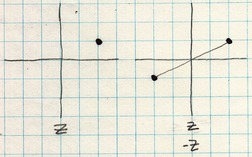
Add the conjugate and its opposite: z*, and -z*.

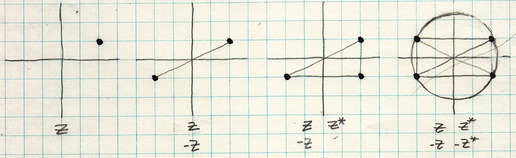
It is the conjugate operator that gives the imaginary axis away. The imaginary axis is vertical [Correction: z and z* are on the right, one with a +imaginary, the other with a -imaginary. Therefore the imaginary axis must be vertical]. Because each of these is algebraically distinct, they must be visually distinct. Consider that a rule to live by.

Think about rotations in the Argand plane. Multiply the number by 1, and z stays in its home. Multiply z by negative one, and both real and imaginary numbers flip, causing z to play hopscotch over the origin, a pi sized rotation:

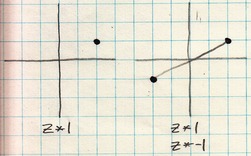
Multiplying z by the imaginary number i causes a rotation by 90 degrees. Minus i does a rotation the other way. Here is what that looks like:

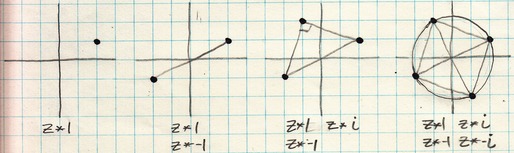
Notice I did a deliberate science faux pas: I did not label the axes. Oops. It is not possible with just rotations to say if the imaginary axis is horizontal or vertical. We do know that real and imaginary numbers are algebraically distinct, but visually there is an issue here.

Some will complain that there is not enough information provided.
 Consider my sketch of Michelangelo’s David. This did not require 2 years of effort to make a 17 footer weighing 6.4 tons. Art is lost in the reduction.

I would argue that a similar thing happens in mathematical physics. Sure, the equations get fancy, but not the images. One must draw the basics right before drawing anything fancy. Everyone says all axes must be labelled. I have always operated that way. But think about Nature. Are there any axes, let alone a labeled axis? No. Can you tag an electron to keep track of it? No, all electrons are indistinguishable. Does Nature actually use complex numbers? Yes, all the time in quantum mechanics. If we want to represent complex numbers accurately as Nature uses them, the visualization cannot require labeled axes or tagged points (really the same thing).

Our visual systems are fantastic at analyzing things that do not move. This is why artists use easels. Visual memory is crap, but a well-placed easel allows the artist to quickly compare their work to the model. This matters to realist painters, not abstract expressionists.

When I started making the quaternion animation software, I found out I couldn’t understand what was going on. Anything subtle was sure to be lost in the motion. Including the three Argand planes with their labels was important since those don’t (quite) move. I did put some effort into making a line that sweeps across the plane in exact timing with the animation because the motion would tell the viewer which axis was time.

Let’s start simple with a line of events moving steadily from -2 -1 -2 -3 to the origin.

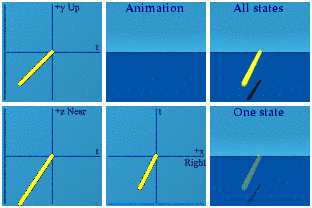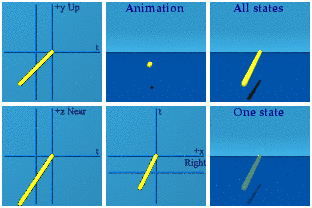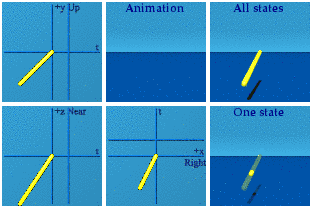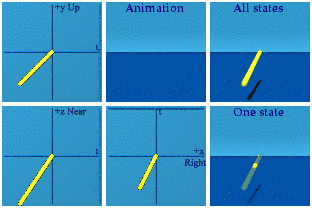
Nothing exciting, move along.

Flip the sign on the scalar.


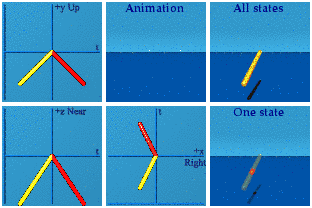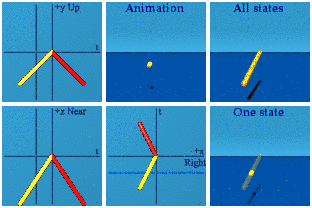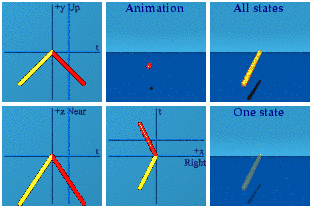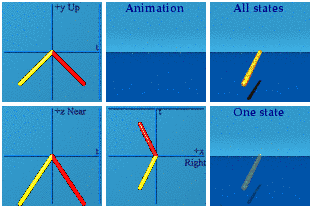
How the point gets to the origin determines how it backs out from the origin. Doing a time reversal requires you remember what went on. Only a good memory allows a system to do real/time reversal.

Look at the look of a conjugate in an animation.

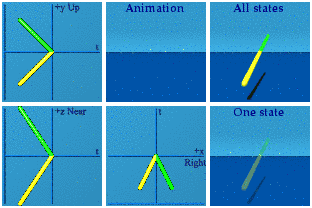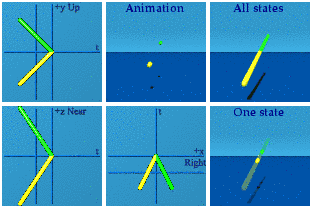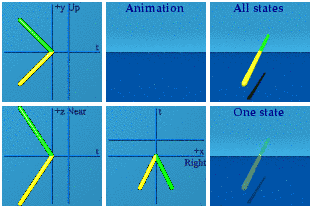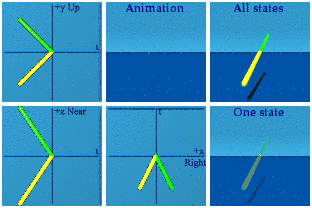
This is a mirror operation. There are two points on the screen. This is how a conjugate is visually distinct. No one can confuse a reflection over the real/time axis with one for the imaginary/space axis. Ever. The real axis reflection requires memory, while the imaginary uses a mirror so one can see double.


For completeness, here is the complete set.


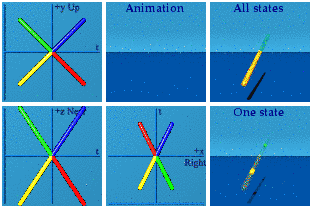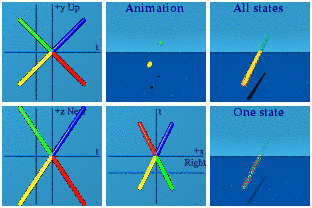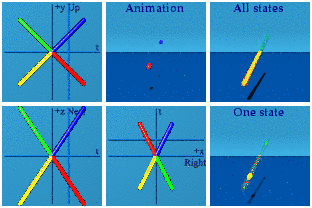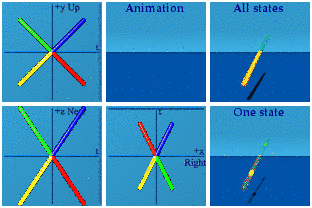
It takes some practice, but can be fun to identify which one is which as the animation loops.

Let’s see this in action. Here is a 3th order quaternion polynomial animation with quaternion coefficients:

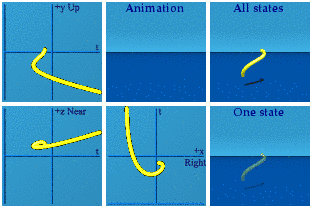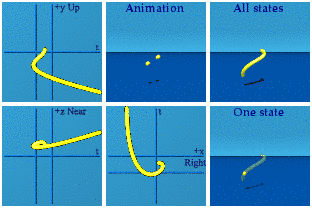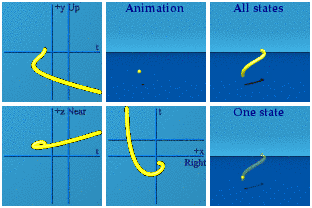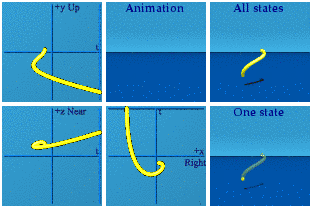
It darts around spacetime in ways I would never have guessed. Look at a reversal in time versus a reversal in space, I’ll let you figure out which is which.


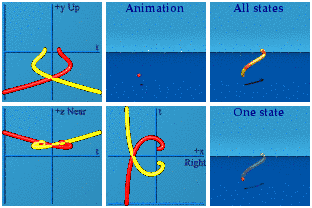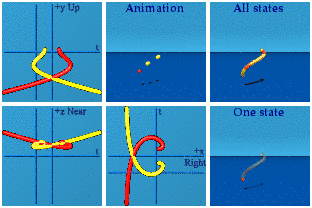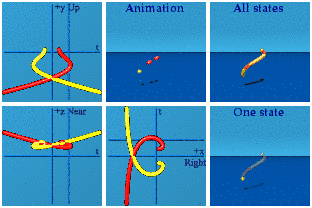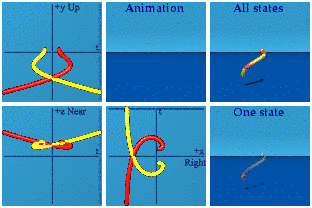
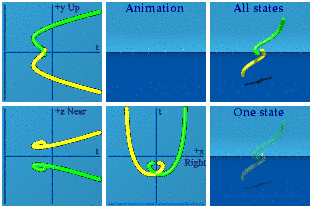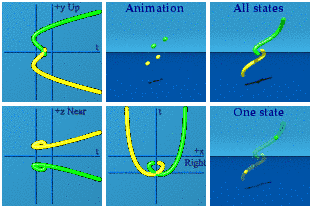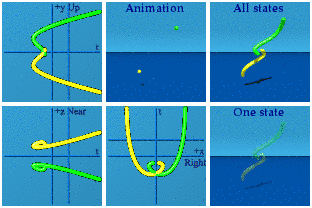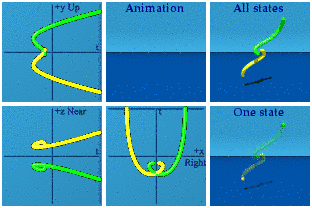
I'll let you decide which one looks more erotic in the complex planes.

Not only are real and imaginary numbers distinct algebraically, but with the aid of animations, they are distinct visually. If someone asks what the difference between real and imaginary numbers are, analytic animations provide a new answer. Real numbers are time is money. Imaginary numbers are space is real estate. Money and real estate work together, but are two different things. Reversing reals requires memories of the way we were. Flipping imaginaries employs a fun house of mirrors. Reals and imaginaries are separate: reversing time does not change how one looks in a mirror, only behavior. Watches in mirrors still go forward even if the hands are confused.

People writing books focus on static images for obvious reasons. Nature is dynamic. It is about time to update our view of the complex plane from a book shop in the early 1800s to Science 2.0. Join the evolution.

Doug

Snarky puzzle

‘Ever’ only lasts until a counter-example is found. A circle in the complex plane has so much spacetime symmetry: it goes out as it comes in, and there are always two points. Discuss how you can find the origin, where and when it is.

Next Monday/Tuesday: Why Quantum Mechanics is Weird