 using roughly 40% of our CPU. We don’t ask movie stars to understand spread-spectrum communications technology, unless they do, like Hedy Lamarr.
using roughly 40% of our CPU. We don’t ask movie stars to understand spread-spectrum communications technology, unless they do, like Hedy Lamarr. DNA is a sexy molecule. It has all those curves. Walk into any new biology building, and you are sure to see the double helix motif. DNA has a direct involvement in sex. A human sperm is [correction: 3] billion bases of DNA, two energy sources, a motor, and tools to break into an egg, so long as that one sperm is first.
DNA is a sexy molecule. It has all those curves. Walk into any new biology building, and you are sure to see the double helix motif. DNA has a direct involvement in sex. A human sperm is [correction: 3] billion bases of DNA, two energy sources, a motor, and tools to break into an egg, so long as that one sperm is first.The standard model is not sexy. Walk into centers of theoretical physics, one sees blackboards, tasteful furniture, coffee machines, and pictures of previous pioneers of physics who gained their stature via
the elegance of their contributions. In a year long relativistic quantum mechanics class I took at Harvard University, the standard model as a topic came up once. The professor was disdainful, treating the standard model like an ugly date. He didn’t want to be seen by anyone discussing the arbitrary collection of three groups.
[click or skip a reading of this post]
The visuals we have are dull. The group U(1) is a circle in the complex plane. I considered including an image, but why bother? Should I date a dull girl? Maybe I should date that redhead who when she skips her meds has been arrested for lewd public behavior? Dull girls get no respect.
Visuals are missing. The group of unit quaternions, SU(2) should be viewable since only three numbers are needed for its Lie algebra. Some might speculate that we can never see SU(3) which needs eight independent generators. Requiring eight independent generators is not the same as requiring eight spatial dimensions.
In this blog, the plan is to animate the continuous symmetries U(1), SU(2), U(1)xSU(2), and SU(3) [almost]. I can do this because I built a tool to animate any algebraic quaternion expression. Since I am a biologist, I use C and Perl as programing languages - C is fast, Perl can stick this with that (“Why not put a duck bill at the end of this platypus?”). The interface chosen was the only one that has lasted since the 70s: the command line. Here is a sample calculation:
% q_add 1 2 3 4 5 6 7 8
6.0000000000000000 8.0000000000000000 10.0000000000000000 12.0000000000000000
It is simple enough to generate thousands of numbers with ~90 small programs.
How does one create a 4D image, is that possible? No. The questions shows one is thinking of 4D as 3D plus another D. We don’t live in 4 spatial dimensions. Special relativity taught us we live in spatial 3D and scalar time. What I can do is generate analytic animations. This is an update of Rene Descartes’ analytic geometry. I found out that my visual memory is so bad, the animations did not make sense. I had to surround the moving picture by a few static ones.
Start off dead simple: quaternion addition.
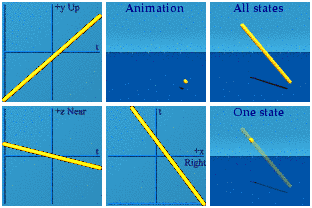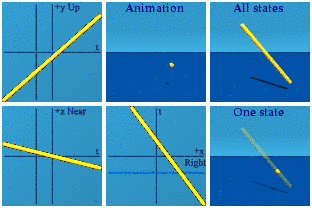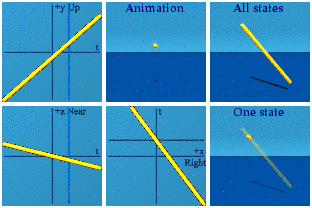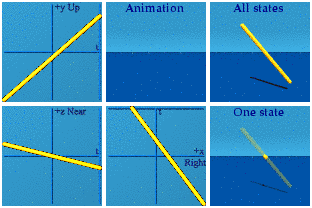
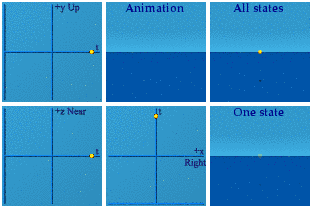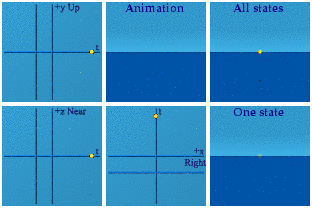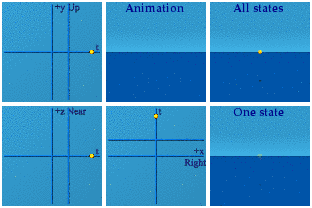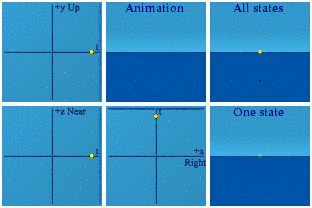
This is one of the few analytical animations I imagined right. Simple quaternion addition is directly related to a deep idea of special relativity: the inertial observer. I am too much of a minimalist. For this blog, I added the 6 labels: Up, Near, Right, Animation, All states, and One state. That almost makes these self-explanatory. The animation is front and center. On the left are three complex planes, up/down+time, near/far+time, and right/left+time. In the upper right is All states, every state the system goes through during the animation. That was inspired by the wave function of quantum mechanics. Below it is One state, a random sampling from All states. The collapse of the wave function anyone?
The animation loops, or I have set periodic boundary conditions if you choose to be technical. I often need to watch for a while to see all that is going on.
The basics of trigonometry are the circle and the triangle.
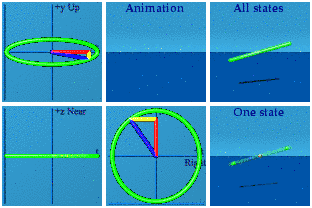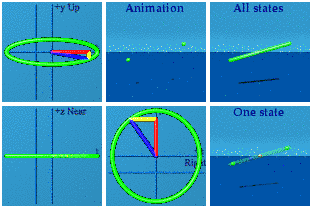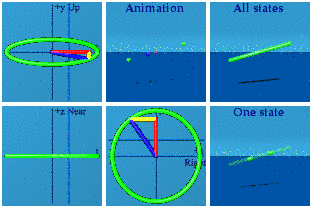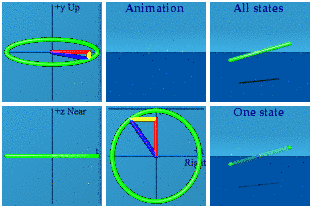
Animating these simple objects is strange. Look how straight the line is in space. That is how it goes. The circle and triangle are about space and time, not space and space. We have all drawn circles and triangles in space and space since a young age. An animated right triangle can be created by holding your two hands together, then letting one move away at a constant speed, then clapping instantaneously (OK, not possible, this is only an approximate right space and time triangle).
Drawing an approximate space and time circle with your hands involves separating your hands fast, then slowing down when they get apart, so they can rush together for a clap. It may be an acquired skill to draw the space and time circle accurately, as is the case for a space and space circle.
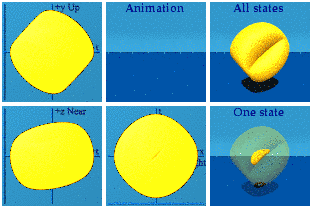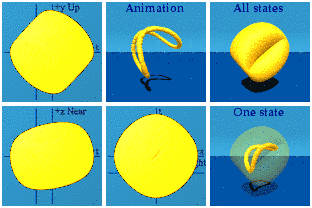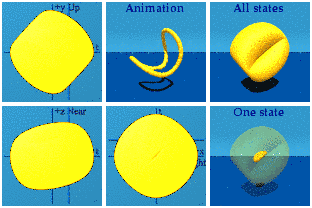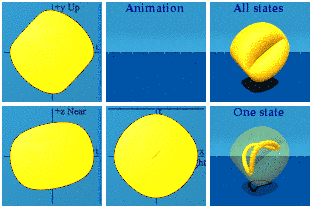
Those are the basics. The Abelian group U(1) has already been done: it is a circle created by normalizing a quaternion.
[CORRECTION: this is a way to represent the group SU(2), not U(1). I will call this the norm representation of SU(2), and put that label in brackets subsequently. To represent U(1), alpha must be a complex number, which can be done with quaternions since complex numbers are a subgroup of quaternions. See discussion below with David Halliday.]
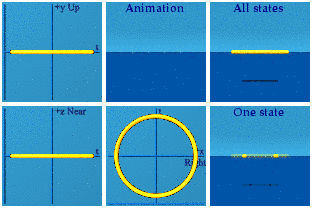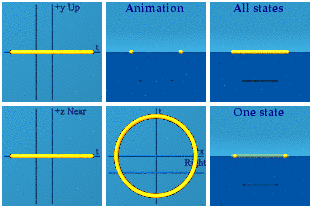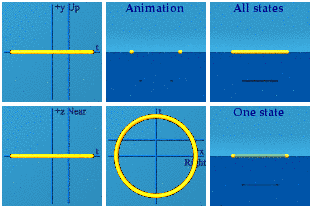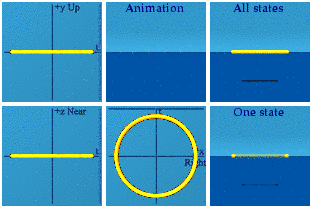
The group SU(2) is also known as the unit quaternions. One way to represent it is with this expression:
This animation should look familiar:
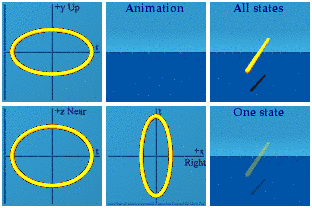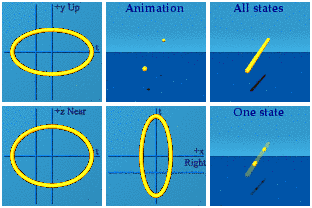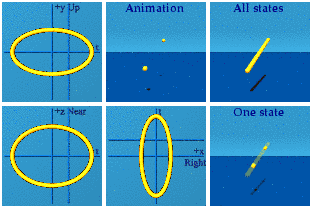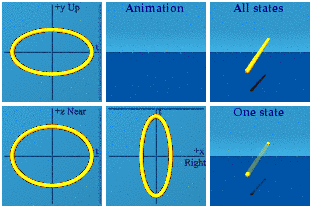
It looks so similar to [the norm representation of SU(2)] one might think they were exactly identical. Time makes the situation subtle. It is hard to see differences in time. When do things start happening in time for [the normalized SU(2) representation] versus [the exponential representation of] SU(2)? For [the norm representation], that can start anywhere from -1 to a positive 1. I took 50k events, normalized those, then made this animation:

Nice and uniform.
The same cannot be said of the [exponential representation of] SU(2):

There is nothing, then a little something at 8 points, that grows into a sphere, that shrinks back down to nothing. It is Ms. Pacman on mushrooms. Think of the Taylor series for an exponential. If the exponent is super tiny, it is (1, 0, 0, 0) minus a correction. As long as the 3-vector is tiny, all will huddle around the spatial origin at time=1. The only way to fight world-wide domination of time is for the 3 spacemen to join hands in all 8 positive and negative combinations. That is how the animation starts out.
% q_exp 0 1 1 1
-0.1605565385746905 0.5698600991825139 0.5698600991825139 0.5698600991825139
% q_exp 0 1 1 -1
-0.1605565385746905 0.5698600991825139 0.5698600991825139 -0.5698600991825139
The animation grow to a maximum value whose value I have never determined.
Three stories about Ms. Pacman. This animation was the reason I bought an iPod. I wanted to carry this insight with me. It was that fun, pretty, interesting, like a good date, that I wanted to show off. I went into an Apple store to see if the gif animation could be displayed (some modern cell phones cannot deal with gif89a). I went to the Genius Bar and was quickly told to see a sales person. That person was helpful. I explained what the image was and he asked for my business card.
Sheldon Glashow won a Nobel prize for his contributions to electroweak theory. He works at BU. He was set to give a talk at a local university. I emailed him ahead of time to say I had an animation of SU(2) I would like to show him after his talk. He did his thing, and I walked up with the Powerbook turned on, Ms. Pacman doing her create and destroy thing. I asked if he wanted to see the animation. He declined. I guess he has been approached by too many fringe physicists.
The third story is a confession. I admit that I have said in many places that Ms. Pacman is a visual representation of the group SU(2). It is not. The simple circle animation is a representation of SU(2). I was driven by the hope that SU(2) would not be a dull girl. I know I found that one first, but it looked too simple. Tossing random numbers at an exponential looked wild. Once I have a good way to describe the relationship between Ms. Pacman and SU(2), I will have to put a “CORRECTION” label in quite a few places. At least then I will be more right than I was before.
On to Glashow’s area of expertise, what U(1)xSU(2) really looks like...I don’t have to show it, do I? It must look like the other two. For electroweak symmetry, form the product.
At the start, all points are reachable, but there is a bias for points in the past. This is due the bias to +1 from SU(2).
I spent over a year puzzling over how I might represent the group SU(3) using quaternions. Its Lie algebra has eight generators, which sounds like four plus four. One can multiply two electroweak symmetries together, and that will generate another member of the electroweak group. That is how groups work. This was a pea under the mattress problem, something to bug me from time to time, to revisit until the right answer appeared. What needs to change is the multiplication table. All that needs to be done is to take the conjugate like so:
The math wonks in the house will pick up on the fact that multiplication is no longer associative. A group is associative, ergo this representation is a failure. That is why I put in the approximate sign. This is almost the group SU(3) except it is not associative. Let the investigation continue.
I am not sure I should show the animation of SU(3). One expects dull girl to be dull, that is all you have seen. I don’t work with Harvard professors with a great disdain for the standard model. Instead I have worked with a dull type of number for more than a decade. I did go to the Second Meeting on Quaternionic Structures in Mathematics and Physics in Rome in 1999, but the third meeting did not happen five years later, I was looking for it. Ever since I bought quaternions.com I hear from sincere folks that I should drop the focus on the dull girl and go do calculations with some more popular type of number. Do you want to know why I have remained faithful to dull girl? That is my own decoy. There is no dull girl, there is only a fascinating woman. It has sometimes taken me years to figure out how to ask her a question. Every time I have been rewarded by wonderful insights. If I have to be the only one hanging out with this woman who is so much more than a one trick 3D rotation pony, fine by me. I have data that says Nobel prise winners don’t care about her which is great, more face time with me. Here is the quaternion representation of the group SU(3):
This has curves, cleavage, and grace. The standard model is sexy.
Nothing but unity. This lady is sophisticated.
Doug
Software available via:
git clone git://quaternions.git.sourceforge.net/gitroot/quaternions/quaternions
Commands used to generate the animations:
q_graph -dir sm -out addition -width 180 -height 180 -overwrite -box 2 -command 'q_add_n -2 2 -2 .5 .004 -.003 .0035 -.001 1000'
q_graph -box 1.3 -dir sm -out timelike_future -overwrite -command 'g_u1_n 1 -.7 -.2 0 2000 | q_x_scalar 1.23693' -color green -command 'constant_linear_motion 100 0 0 0 0 1 0 0 0' -color red -command 'constant_linear_motion 100 0 0 0 0 1 -.7 -.2 0' -color blue -command 'constant_linear_motion 100 1 0 0 0 1 -.7 -.2 0' -color yellow
q_graph -width 180 -height 180 -dir sm -out u1 -box 1.2 -overwrite -command 'g_u1_n 1 2 3 4 1000'
q_graph -width 180 -height 180 -dir sm -out su2 -box 1.2 -overwrite -command 'g_su2_n 1 2 3 4 1000'
q_graph -width 180 -height 180 -dir sm -out u1xsu2 -box 1.2 -overwrite -command 'g_u1xsu2_n 1 2 3 4 1000'
q_graph -width 180 -height 180 -dir sm -out su3 -box 1.2 -overwrite -command 'g_su3_n 1 2 3 4 2 -5 -3 2 50000'
q_graph -width 180 -height 180 -dir sm -out su3 -box 1.2 -overwrite -command 'g_su3_n 1 2 3 4 1 2 3 4 50000'
q_graph -width 180 -height 180 -dir sm -out u1_rand -box 1.2 -overwrite -command 'q_random_n_11 50000 | g_u1_n 1'
q_graph -width 180 -height 180 -dir sm -out su2_rand -box 1.2 -overwrite -command 'q_random_n_11 50000 | g_su2_n 1'
q_graph -width 180 -height 180 -dir sm -out u1xsu2_rand -box 1.2 -overwrite -command 'q_random_n_11 50000 | g_u1xsu2_n 1'
q_graph -width 180 -height 180 -dir sm -out su3_one_q -box 1.2 -overwrite -command 'g_su3_n 1 2 3 4 1 2 3 4 1000'
Note: probably over a million quaternions were used to generate this blog due to experimentation. The number actually used is on the order of 204k.
Snarky puzzle. Imagine a spacetime wire cube. No don’t, that is too hard. Do something simpler. Draw a square in three complex planes. Now imagine animating that. Got your picture in your head? Good, now Google for 4d wire cube and be honest about if your imagination matched reality.
Late next Monday: More Sexy Standard Model Animations.
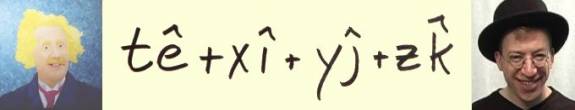


Comments