Snarky puzzle. If you go down in a gravity field, time ticks slower, rulers look longer to someone else. That is 2 changes. Newton’s scalar theory accounts for just one, duh. Write a 4-potential that could account for both g00 and gRR. If you don’t want Newton to do all the lifting, combine a metric with a potential. Since mixing potential theory and dynamic metrics is blasphemy, expect to take a bullet for the team.The Back Story:
Newton’s scalar theory of gravity is useful but wrong. Some prefer to talk about a “domain of applicability”, the collection of conditions required to justify the situations where the equation happens to remain useful. That is the extended dance version of “useful”. Since I am working to find the new new thing, it is important to mark clearly that an expression cannot be the starting place for further growth. I get efforts from fringe physicists who start from Newton and try to make it a little better. Knocking down such work is like shooting fish in a barrel, not enough challenge to be fun, particularly considering how serious the writer happens to be.
click or skip this reading of the blog.
Einstein’s rank 2 field theory for gravity could end up being useful but wrong. I recall once in the moderated newsgroup sci.physics.research having a post with this formal possibility rejected by the moderator as being overly speculative. Moderators should know some history of science, like good science theories get surpplanted by better theories. We don’t know how the universe started (leading hypothesis: inflation). We don’t know why stuff in thin disk galaxies can go at a constant velocity at the edge, or why such a galaxy is stable to a small disturbance on its axis (leading hypothesis: dark matter). We don’t know why current stuff is accelerating more than in the past (leading hypothesis: dark energy). We don’t know how to quantize gravity (biggest contenders: work on strings and loop quantum gravity). The most brilliant physicists on the planet have tried to solve the general relativity/quantum mechanics problem: Einstein, Wheeler, Feynman, Weinberg, Hawking,... Failure, failure, failure...
Why? The most reasonable explanation is that it cannot be done. Good, now I don’t have to try.
If a rank 0 theory is too simple, and a rank 2 theory is too complex, the Goldilocks approach is to try a rank 1 theory. That is skipped in an otherwise excellent review of tests of general relativity. Why? Please wait a week for the blog "Shot in the head", a darn solid reason to write off all my claims, if you know it (spin projection operators of current coupling anyone?)
The Answer:
1. All 4-potential:
2. Half potential, half metric:
The Discussion:
People schooled in GR might give a reflex rejection to equation 1: it has a flat metric, therefore it is wrong. Recall the task at hand: to be consistent with light bending around the Sun experiments. We already know the first term gets the time bending exactly right. There are no terms in Newton’s scalar theory to get the space part right. With a rank 1 field theory, there are new slots to do the job. Those terms are the same size, opposite sign. A 4-potential theory can work for light bending around the Sun experiments.
The monitaur in equation 2,
part Newton, part exponential metric could also get a reflex rejection: where is the demanded elegance? It is like trying to convince erudite wine affectionados to try a single malt scotch. Sure, it would be funny as hell to watch their eyes bug out, but they are not going to appreciate the smooth burn. If I could get them a quarter of the way into a single malt bottle, they will remain at the table because they couldn’t walk straight any more. That’s when I would whisper “duality, duality, duality”. A potential theory can be dual to an exponential metric theory. Let’s drink to duality.July 5 - The Certainty and Uncertainty Principles
Snarky puzzle. Where’s my cow bell? I want more cow bell. People feel lost without their hbar. Add it back to eq. 1. Discuss the silliness of the exercise.
Bonus problem: Make the relationship between position and momentum operators complete. Figure out what is missing - the minus sign in the commutator should give a big clue. When added back in, the greater than sign can be resigned to bad methods in education that will continue for years to come.The Back Story:
I recall John Baez writing that if Planck’s constant were to go to zero, so would quantum mechanics. That idea appealed to me, so simple and direct. Yet when I calculated the commutator in a dimensionless way, poof, Planck’s constant left the stage, sorry JB.
I thought the first question was silly. As I was driving in to work, I wondered where the stuff in the uncertainty equation went when one side was greater than the other. There must be a precise home. That would make a better question.
The Answer:
Add the hbar to the momentum operator so it has units of momentum:
A complete picture is formed from the commutator and the anticommutator:
The Discussion:
When will there be no anti-commutator, or the uncertainty principle be at its minimum? Either x is equal to zero or the wave function is not changing with respect to x at some spot in the manifold, say a minimum, maximum, or inflection point.
July 12 - Julian Barbour Versus Minkowski And Me
Snarky puzzle. Imagine a pair of machines that can measure 1044 dimensionless time to a high degree of accuracy (a little over 5 seconds for you guys still clinging to the bosom of units). One is at sea level, the other at Mount Everest base camp, 5,380 m. Calculate the square of both of these intervals (the formula with standard units is delta t = -t G M h/(c2R2). Imagine a bullet train going at 3 x 10-7 (a little over 200 mph) along one axis gets data from both clocks. What would they report?The Back Story:I was in a physics-babbling stage at Christmas, 1988, when both my mother and sister bought Steven Hawking’s “A Brief History of Time”. One of my ideas from that time was that all of physics should be dimensionless. It is like working with the Reynolds number on steroids. I finally realized how to implement the project: if everything going in is dimensionless, then the output would be dimensionless. Take a time in seconds, and divide it by Planck time in seconds. Since Planck units are tiny, that makes ordinary time a HUGE number. Derivatives with respect to either time or space are going to be teeny tiny small because they are a product with Planck time and space respectively. Change doesn't happen, approximately.
What made this assignment fun is that I knew I would feel uncomfortable with the numbers getting plugged in. The numbers would feel alien. Oh well, too bad.
The Answer:
The relevant equation and values:
The train reports the same interval.
The Discussion:
A time of 1031 is tiny, about a half a pico second. It surprised me that a few dimensionless unit of time are larger than the mass of the Earth or the height of Everest. We can let the philosophically inclined reflect on that observation.
July 19 - Sex And Unified Field Theory R&D
Snarky Puzzle. Think about the animation of (1,0,0,0). Compare and contrast that with animations of (0.9, 0, 0, 0) and (1.1, 0, 0, 0). Reflect on the standard model symmetries in curved spacetime.The Back Story:
There is something I will call the standard model standard conspiracy. I know people who work with the standard model know this, but they don’t talk about it, or at least don’t talk about it around me. One thing I have learned about computer programming is that one should not put in constants by hand, use variables instead. The standard model has three different groups: U(1), SU(2), and SU(3). The S stands for special, having a determinant of 1. The norm and determinant of U(1) is also equal to one. Or to be pedantic, the norm of all three look like this:
That is a special number with all those zeros from here to eternity.
The pros will probably crow that is just unitarity. Make sure the probability works out to 1, exactly. I embrace that my measurement of unity is like your measurement of unity. A central lesson of special relativity is that if I compare my sense of any number to your sense of that number, we either agree because that number is Lorentz invariant, or disagree in a way we can calculate (Lorentz covariant). I suspect the norm is invariant under a Lorentz transformation because it is a ratio, with both numerator and denominator changing in the same fashion.
It is my belief - and it is a belief, not backed up by analysis - that gravity may alter how one part of the spacetime manifold assesses the norm of a different part of the spacetime manifold. Here is my animation of SU(3) which contains the subgroups SU(2) and U(1):
50,000 quaternions were used to make these 25k members of SU(3), basically A*/|A| B/|B|. I should have used more to make the animations continuous, sorry. The time squared plus space squared always exactly equals one. Someone else in a different place in a gravitational field would create an identical animation of the group. If one were to compare three spheres with radii of 0.9, 1.0, and 1.1, they form a dynamic ice cream cone:
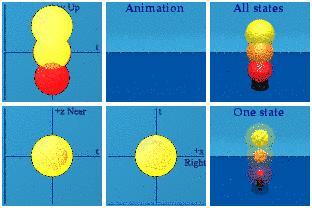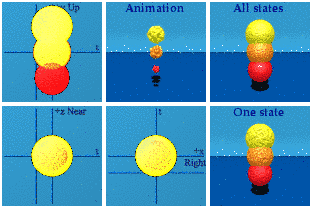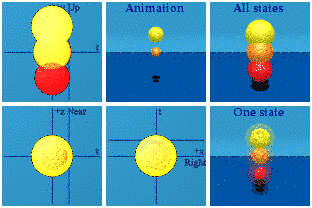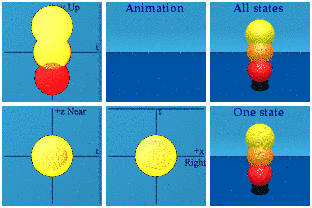
Notice the red sphere starts last, finishes first, and has the smallest radius. Likewise, the yellow starts first, ends last and has the largest radius. A larger norm means larger in time and space.
The Answer:
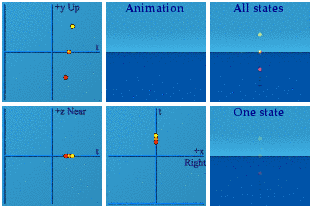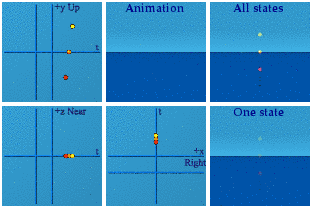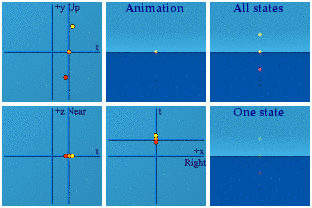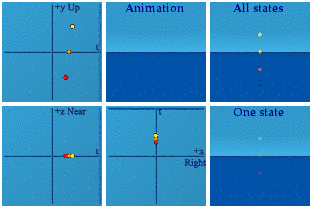
The Discussion:
What does gravity do vis-à-vis the standard model? On numerical grounds, the experimentalists going through inverse femtobarns of data do not have to be concerned. It is only folks worrying about how gravity plays nicely with the other forces of nature that should be concerned. Gravity is a theory that must have a metric explanation, a metric as in ruler. The earlier puzzle claims a 4-vector potential theory is dual to a static exponential metric theory. How big is the ball? As far as the person at the center of the ball, it is always unity because breaking unitarity is not allowed. It also does not make sense: whatever happened can be mapped to that sphere. When two of these probability beach balls are compared, they can be different. That’s how I view the Pound-Rebka experiment done down Route 2 in Cambridge, MA. The iron in the basement and the iron in the attic beat their unitary drums at different rates.
Doug
Google+ hangout: 11:00-11:45pm Eastern time, Tuesday-Friday. http://gplus.to/sweetser
This could be an efficient way to exchange a few ideas. If you have a question or two, hangout.
Bet against the Higgs being found, buy the t-shirt
Next Monday/Tuesday: Shot in the Head
Comments