 I think of myself as non-violent, a purple guy in the blue state of Massachusetts.
I think of myself as non-violent, a purple guy in the blue state of Massachusetts.When it comes to proposals in science though, I go for head shots. Nature doesn’t care if we keep repackaging bullshit. A well-fed bull does not run out of bullshit.
To stop a science zombie, a bullet to the brain is all that might stop it. I know from experience that the easiest person to fool is myself. I am on the lookout for bullets for subjects I speculate on.
I am a poor student of my own personal history, so this is only an approximate timeline. In 1997, I got interested in quaternions based on a contest I came up with to state a brief definition of time. In 1999, I was the second person to find a road to the Maxwell equations using combinations of symmetric and antisymmetric quaternion operators. The complexity of that result led to my first expression to unify gravity and EM - ignoring the weak and strong forces as many do but should not. Right before my 20th high school reunion, I found a tenuous road to the exponential metric.
I loved the exponentials, the calling card of deep insights in physics. The metric is consistent with weak field tests, but differs from general relativity at the next level of precision.
Experiments for the first order bending of light at the edge of the Sun pitted Newton’s scalar potential theory of gravity versus Einstein’s rank 2 metric theory. The predictions were different by 100%: Newton with the low bid of under an arcsecond, 0.875. Einstein doubled down, predicting 1.75 arcseconds for the bending after a paper initially agreeing with Newton. The first results from solar eclipse experiments in 1919 gave Einstein the victory. It took radio astronomy work without the need for eclipses to solidify the case. Newton’s scalar potential theory has but one term to warp time, effectively the g00 term of a metric. Einstein had another, equal contributor that bent space. Pessimist say Newton’s theory got it wrong. Optimists say the prediction is half right.
Second order light bending requires a measurement a million times more sensitive. That experiment has not been done yet. The Schwarzswchild metric predicts an additional 10.8 microarcseconds should be viewable. If the exponential metric rules the heavens, then the experimentalists will see 11.5 microarcseconds more bending, a 6.6% difference. The state of the art measurements are about 100 microarcseconds, a 10,000 fold improvement over 1919, but still needing a hundred fold improvent. The fact that the Sun spins and has a quadrapole moment could obscure the difference.
I spend years on SPR (sci.physics.research) pounding the drum for the exponential metric. It was a solution to a differential equation! It was consistent with current tests! It was different at higher resolution! I thought that triple play would be enough to elicit interest. Triple plays are rare. I had a specific testable hypothesis while work on strings to this day does not. Alas, people are into their own areas of study, or their kissing cousins. Rank one proposals for gravity are the work of idiot savants, without the savant part.
In 2004, I found a bullet with the exponential metric’s name on it. I had my funky derivation of the metric which relied on a perturbation solution of a potential equation, plugged into a force equation, rearranged to look like a metric. I also had field equations “Done the right way”™, derived from the Lagrange density. I had yet to take the exponential metric and see if it solved my field equations.
I recall a particular walk from 1340 Comm Ave to my gym.

I had only a vague idea how to "take the exponential metric and see if it solved my field equations." I didn't sweat those details. I was worried about the results of any calculation. Let's say I did figure out how to plug the exponential metric into the field equations and the result was plain old wrong. That got me sweating before I reached the gym. I had been talking about the exponential metric for years.
 I remember the realization I had right in front of Natalie's Pizza: if the exponential metric does not solve my field equations, then I would have to announce that negative result on sci.physics.research and on my web site, quaternions.com. Nice clear line of action, but there was backlash in my brain. I wouldn't really have to do that, would I? Yes, I would. Think about anyone else reading up on my claims in SPR about the exponential metric. If and when I found the flaw, I would be obligated to describe it in order to save others from wasting effort in this direction. By the time I reached the gym, I knew I would have to fire a bullet at the exponential metric and report the result.
I remember the realization I had right in front of Natalie's Pizza: if the exponential metric does not solve my field equations, then I would have to announce that negative result on sci.physics.research and on my web site, quaternions.com. Nice clear line of action, but there was backlash in my brain. I wouldn't really have to do that, would I? Yes, I would. Think about anyone else reading up on my claims in SPR about the exponential metric. If and when I found the flaw, I would be obligated to describe it in order to save others from wasting effort in this direction. By the time I reached the gym, I knew I would have to fire a bullet at the exponential metric and report the result.For three weeks, I did nothing. I was waiting for my mind to settle down. I also did not know how to do the calculation. There was a disincentive to learn how to do a calculation that would lead to a report of failure of four years of work. This was not about me though, it was about Nature. She does so much simultaneously in silence. I was in the deep end of the pool. I didn’t have any swimming buddies as happens in graduate school. At least I was not in the basement, living on the second floor at the time, with a view of 1325 Comm. Ave., Aerosmith’s place in Boston.
Let me set the stage, kinda knowing the calculation to do, but missing some essential details. The first of my four field equations is a variation on Gauss’s law:
Only the sign on the Laplace operator changes. Fringe physicists before me have constructed a mountain of Maxwellian-gravity crap. I understand why many a pro will avoid this sort of expression. In the static case, the equation is exactly Newton’s law of gravity in the potential form:
This is the sort of problem given to high school students starting out in calculus: show the charge/R potential is a solution to this differential equation.
Now imagine the potential is constant. Can you find a solution if the charge density is not zero?
This sounds like a trick question. There is nothing to do if the potential is constant. That is the case with the tools provided in high school. The derivatives they teach are all about the function and how it changes. A completely reasonable place to begin an education.
Mathematicians thought about taking derivatives if the background geometry was changing. In that case, one would use a covariant derivative. A covariant derivative has the normal derivative plus something called the connection.
The partial derivative is the one from high school. The gamma is the connection which accounts for how the geometry changes. Math heavyweights can play all kinds of games with the connection. I used the playbook of general relativity. The connection there is metric compatible and torsion free. I spent 4-5 quality months with Sean Carroll’s “Lecture Notes on General Relativity” to get a sense of what those technical constraints mean. The bottom line is that the connection bears the name Christoffel symbols of the second kind. Sounds like a movie by Steven Spielberg.
We live in nearly perfectly flat spacetime. To be super right, I could view the Laplace operator as two covariant derivatives. I was skeptical of that approach, remembering the lesson of early quantum mechanics where if one used two relativistic derivatives, the equations did not describe a hydrogen atom. For almost perfectly flat spacetime, I thought I should take the normal divergence of a covariant derivative of a potential:
The Christoffel take three first order derivatives of a metric. A divergence of a Chrisoffel will thus take a second order derivative of a metric. This is the minimum required to constrain a metric by physical conditions, a second order differential equation. Think of it like Newton’s second law for spacetime geometry.
This is where I was stuck for three weeks: I had never calculated the Christoffel symbol for any metric. I was not sure I was going to be able to do the calculation. Plus I was scared of the result. I recall it was a nice Saturday morning. I was wondering what to do, and then I remembered the calculation. Time to crack open a book. I happened to have good luck understanding “Gravitation and Spacetime” by Ohanian and Ruffini. The index leads to a definition soon enough:
Ouch. I started reading around about Christoffels. I found out that one of these three derivatives can be ignored if the metric is static, nice. Another can be ignored if the metric is diagonal, nice. The derivative of an exponential is one I can still remember decades later:
The inverse of the exponential metric will put a minus sign in front of the exponential, so
Nice. The exponent is charge/R, so the divergence is something like:
Bingo, bingo. This is something Laplace would recognize.
That is the sketch. Details can kill, like one sign error. I have run the exponential metric through Mathematica using functions written by James Hartle. It is section 4, page 7 in html , a pdf or notebook, if you wish to cross check. Just as important, I told a friend to see if he could independently confirm this observation about the exponential metric in Gauss’s gravity law. He came back and said no, it did not work. I went over the details with him. He had done two covariant derivatives. When he did just one, it worked.
I have a memory of reading in one of my GR books that one should never bother to take the divergence of a Christoffel symbol. The calculation is banished because a Christoffel doesn’t transform like a tensor. Fortunately I am doing something different. I am taking the divergence of a covariant derivative of a 4-potential. The 4-potential is constant while the metric is dynamic, thus reducing the problem to the divergence of a Christoffel. Did I tell you my father went to Harvard and Harvard Law as did his father? I got wait listed, so went to the tech school down the road, my first choice.
What is cool about this observation is that Newton’s old scalar potential law for gravity can be expanded to a 4-potential. Do gravity as a potential theory or as a metric theory, the choice is yours. The exponential metric is not a solution to the general relativity field equations. In 1919, Einstein’s gang of 10 equations beat Newton’s scalar theory. In 2011, a 4-vector Newton could challenge Einstein for a rematch. This time Newton predicts more bending. Go new Newton.
The exponential metric survived the potentially deadly calculation.
Doug
Snarky puzzle. If you go down in a gravity field, time ticks slower, rulers look longer to someone else. That is 2 changes. Newton’s scalar theory accounts for just one, duh. Write a 4-potential that could account for both g00 and gRR. If you don’t want Newton to do all the lifting, combine a metric with a potential. Since mixing potential theory and dynamic metrics is blasphemy, expect to take a bullet for the team.
Next Monday/Tuesday: The Certainty and Uncertainty Principles
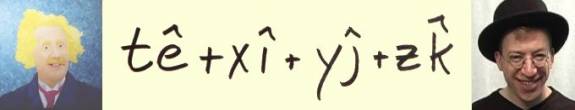


Comments