The Road Not Taken
By Robert Frost
Two roads diverged in a yellow wood,
And sorry I could not travel both
And be one traveler, long I stood
And looked down one as far as I could
To where it bent in the undergrowth;
Then took the other, as just as fair,
And having perhaps the better claim,
Because it was grassy and wanted wear;
Though as for that the passing there
Had worn them really about the same,
And both that morning equally lay
In leaves no step had trodden black.
Oh, I kept the first for another day!
Yet knowing how way leads on to way,
I doubted if I should ever come back.
I shall be telling this with a sigh
Somewhere ages and ages hence:
Two roads diverged in a wood, and I—
I took the one less traveled by,
And that has made all the difference.
Special relativity is special because it applies exclusively to inertial observers.* Einstein turned to his friends that were better than himself for the math to work with arbitrary observers. The answer: use Riemannian geometry. And so physics has proceeded using tensors, metrics, connections, and differential manifolds ever since.
* As pointed out in a comment below, this sentence is technically in error. I should have said "Special relativity is special because it applies exclusively to flat space-time." In my limited defense, I was thinking about the years shortly after 1905 where the discussion was about going from observers who traveled at a constant velocity to those that could move arbitrarily through space-time. The idea of flat versus curved space-time took years to develop, and a little longer still to handle mathematically in a correct manner.
As readers here know, I have had a long-standing interest in a different path. I have studied the math of quaternions, playing a game of seeing how many equations written the standard way I could recast with quaternions. I have had better luck than most in this game. One failure was to recast the Riemann curvature tensor in a quaternion form. That is too crazy-big a project for a part-timer like myself. I have a profound respect for all the work done with differential geometry which is utterly enormous.
This Spring, I reconsidered Einstein's plight of generalizing special relativity. Say there were two events separated by a time dt and a 3-vector space of dR. Write that as a quaternion and square it:
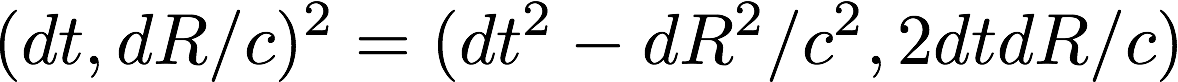
I am going to call this the "reference square". The only thing that makes it the reference square is that it is made by the reference observer. There is no constraint on who gets to be the reference observer other than there is only one such observer. For example, the reference observer could be in a gravitational field and thus not an inertial observer.
The first term in the reference square is the Lorentz invariant interval of special relativity fame. And the second, third, and forth terms - they don't even have a name. Even today, I find that striking. This spring I came up with a name: space-times-time. Perhaps I should have called it time-times-space since I always write it dt dR, but the order does not matter, and I like its overlap with space-time.
Now imagine another observer who was able to look at exactly the same events. Let them use whatever coordinate system they want. Let them use whatever units they want. I put no constraints on observer #2. She goes and calculates the square. We ask her to report the results in Planck units. Let consider the situation where the interval reported by the woman are exactly the same as calculated by the reference observer, although the space-times-time has a different norm. We can say something precise about the reference and observer #2: they are moving at a constant velocity to each other. If the norm of the space-times-time was larger for observer #2, she would be moving away from the events more than the reference observer. If the norm was smaller, then the motion is toward the action. If effort was made to assure the coordinate systems used were the same, then it becomes an algebra problem to figure out exactly how one observer is moving compared to the other.
A third observer watches the same events as the reference observer. This time the interval calculated is not the same.
Recognize the implications of this simple case: a quaternion squared can manage all possible cases of non-inertial reference frames. The third observer could be accelerating in an elevator, going on a Ferris Wheel, hanging out in a different location in a gravity field. All of these will cause the first term of the square to be different from the reference observer.
The deepest insights in Nature involve simple invariants. With special relativity, the first term of a quaternion squared is invariant for all inertial observers.
Here is my quaternion gravity proposal: the norm of the space-times-time terms of a quaternion squared is an invariant for all non-moving observers* under the influence of gravity.
* By non-moving observers I mean for a pair of observers, then is no constant-velocity transformation needed to go from one observer to the other. Recall the tests of general relativity where one clock was flown in a plane while the other stayed on the ground. To account for the changes seen, there were two effects: the speed of the plane and the different location in a gravitational field. What I am saying is these pair of observers have no plane or other form of motion between them to correct so it is all gravity.
| dt2-dR2/c2 | |2 dt dR/c| | |
| constant velocity motion | invariant | varies precisely** |
| Influence of gravity | varies precisely** | invariant |
We know this is approximately true for the Schwarzschild metric of general relativity, but not exactly. Gravity changes the measurements of time and space by factors of GM/c2R, but for one term the coefficient gets smaller (time) while the other coefficient gets larger (space). The product of those two has a squared GM/c2R term, small stuff.
Special relativity has no field equations to solve. Special relativity, as an algebraic constraint, applies to everything. Similar features are true for quaternion gravity. One implication is that there is no graviton. Because there is no graviton, there is no problem quantizing gravity. "That was easy."
Solving the ten non-linear differential field equations of general relativity is a deeply daunting task. Finding functions that will be consistent with quaternion gravity by contrast is trivial: multiply the space terms by one function, and multiply time by its inverse. That is a low bar to clear.
What function - and its inverse - should be involved to conserve space-times-time for a spherically symmetric, uncharged, non-rotating mass? This was the first solution found to the field equations of general relativity by Schwarzschild. We know it must depend on that ratio, GM/c2 R. We know it must go to unity as either the gravitational mass goes to zero or the distance gets very large. Gravitational systems are harmonic. Go with the obvious guess: an exponential function of GM/c2R.
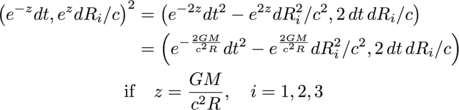
In the literature, the interval shown is the Rosen metric. It is consistent with weak field tests of gravity to first order Parameterized Post-Newtonian accuracy. At second order PPN accuracy, the two differ by only 6%. I am aware there are reports that confirm the Schwarzschild metric to 2.5 PPN, but I think those are tests of consistency since they depend so much on the model of the far away mass. A slightly different model leads to a slightly different prediction. I am not up-to-date on the current state for second order PPN tests. At least this is a testable hypothesis.
The Rosen bi-metric theory fails the energy loss by binary pulsar tests. The extra metric field provides a means to have a dipole mode of emission, and thus not consistent with observation. The quaternion gravity proposal looks like it could have a problem - no graviton means no energy loss by the field.
Remember, there is no field.
That does not mean there can be no energy loss. The function and its inverse do not have to be static. For a quickly rotating binary pulsar, there will be a time component. The energy could be lost via photons whose lowest mode of emission reflects the symmetry of the situation - a wobbling water balloon - a quadrapole moment.
Why?
The short answer is I don’t know. Speculation follows.
Why does special relativity work? My thesis is that quaternions are the right math to use to describe everything, no exceptions. Events in space-time can only be linked by particles that move with a velocity - the ratio of space over time. If those velocities are constant, one gets the invariant interval of special relativity in the square of measurement written as a quaternion.
Most things in the Universe do not travel at a constant velocity, their history a little more complex. Somehow quaternion gravity takes that into account - all forms of non-constant velocity motion.
No idea is new
This issue was raised in a physic stackexchange thread in March of 2011. The original question did not even include the space-times-times terms! The most popular answer was a riff on Clifford algebras which sounds off-topic to my ear. Sure, quaternions are the Clifford algebra Cl(0, 2), but the observation is about the Lorentz invariant interval. Luboš Motl thinks its just a funny coincidence. He too makes the same algebra mistake as the original poster because a quaternion times a quaternion always generates a quaternion. For q* q, people have this habit of dropping the additive identity of space-times-time. Programming with quaternions cures you of this ill because the norm has the same data structure as ever other quaternion. My answer is at the bottom, sitting there all lonely with a zero. Sigh.
Free free to forward this blog to anyone attending or having attended the Convergence meeting at the Perimeter Institute, #piCONVERGE. For that crowd, think about what unity means when one uses quaternions in space-time. It is the group SU(2) which is center stage in the standard model. The group U(1) is a subgroup of SU(2). And as a bit of pure numerology, the group Q8 has eight elements each with a norm of one. Those who have built the graph of Q8 from pipe cleaners know it is not simple.

For commenters
My usual caveats apply. Please stick to the topic of this blog. If you have a new and different approach, go ahead, sign up for Science20, and blog about it. After notification, I will delete comments that break this guideline. No worries.




Comments