The relativistic quantum field equation for a spin 0 particle is the Klein-Gordon equation (written in natural units):
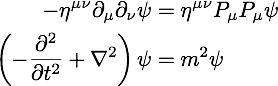
One takes the first derivative of the wave function. Also take three spatial derivatives. Then take the second time derivative of the wave function, and similarly for the three spatial derivatives.
Is this the only sort of second-order changes of the wave function one can study? No. One could take the first-order time derivative of the wave function, then follow that by taking one of three of the first-order spatial changes in the wave function. Technically, it can be done.
My complaint is that the tensor contraction leads to a necessarily incomplete description of the wave function in space-time. If the wave function changes in time and in space which often happens, one must also investigate the mixed derivatives.
Here is a little numerology. The wave function lives in space-time which has four parts to it. The momentum 4-vector has four parts. The 4-derivative has 4-parts. It sounds reasonable to me to expect to see four equations.
One might point out that the D'Alembertian operator really looks like a traditional difference of squares where the cross terms cancel:
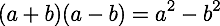
That would be a misleading appearance however since the D'Alembertian is due to a contraction of a 4-vector using the flat Minkowski metric.
A more technically accurate defense would be to point out that the D'Alembertian operator is invariant under a Lorentz boost while a mixed derivative would not be. The description is true, but so what? Consider how a 4-vector transforms. Each of the four terms may transform differently, but what we care about is all four of them together. One could imagine the invariant D'Alembertian combined with three mixed derivatives, call it say the 4-square. With a little effort, we could describe precisely how a 4-square transforms. It is the 4-square that has a chance of being a complete picture.
There is a strong bias for invariants as one dives deeper into theoretical physics. For me, I always, necessarily, need to balance an invariant with something that is not invariant to have a chance at reaching understanding.
Look what happens for example in special relativity. People will talk about how the speed of light is invariant, whether one runs toward or away from the light. That is true. It is also true that both the frequency and wavelength experience a Doppler shift. Those changes are such that the speed of light remains the same. I have heard too many presentations on special relativity that omit the changes in frequency and wavelength. I think it is impossible to understand the invariance of the speed of light without also knowing about the special relativity Doppler shift.
People talk about the changes in measurements with clocks and rulers. It is rare that such efforts to explain special relativity ever mention the Lorentz invariant interval. I consider that to be unfair. The changes in measurements with clocks and rulers are precisely linked to each other so that the interval is invariant.
This is my special relativity manifesto: a complete story always involves things that are unchanged under a Lorentz boost and things that do change. If this is not the story you are told, then you know the story is incomplete. This is why I feel the Klein-Gordon equation tells an incomplete story. The story is not inaccurate - understanding what the D'Alembertian operator does with the wave function is important - but it does not tell the full story.
One way to tell the full story is to abandon tensor calculus and adopt quaternions for all expressions. The core idea is to always keep the same mathematical structure. I devoted a blog to the algebra of quaternions, another to how to calculate intervals. By having the same structure before and after, it is certain information is not ignored, just transformed.
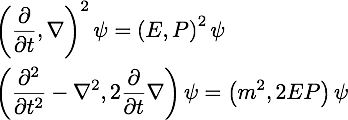[oops, forgot a square, fixed.]The sign police will issue a ticket against this expression. The second order time derivative has the same sign as the mass squared on the other side unlike the certified real Klein-Gordon equation. To me this is merely a signal that quaternions are different from tensor calculus in a precise way that ultimately is not of consequences.
There are people who have built careers investigating if there is information loss in a black hole. Here there are three perfectly well-formed differential operators on the wave function that never are examined.
One could complain that those terms are utterly meaningless in our interpretation of quantum mechanics. I would counter that our interpretations of quantum mechanics are meaningless today. I have seen people do surveys to find out people's preferred interpretation of quantum mechanics. Surveys? In physics? I have in the past, and will in the future, rescind a precise proposal based on a precise critique. The interpretation of quantum mechanics is not a precise idea at this point in history. The leading candidates sound different yet make the same predictions. A 4-square set of equations would make the same predictions using its first equation. The other three would add to the description of Nature.
Has anyone reading this blog made a calculation with energy-momentum, EP? I guess it could be called an energy-momentum flux as it is the product of the two.
[Start wilder speculations]
Here is a technical speculation for why one might want to embrace the 4-square. In field theory, one takes the field equations and inverts them to create the propagator used in quantum field calculations (see "Quantum Field Theory: A Modern Introduction", section 4.3 Quantizing the Maxwell Field by M. Kaku). For field theories with gauge symmetries, that can be done so long as one picks a gauge. If you don't pick the gauge, you don't get a propagator. This happens in EM using tensors because the field theory doesn't come equipped with multiplication and division. With quaternions, the operators form a product with the wave function. As such, it can also be multiplied by more operators, specifically the inverse of the 4-square. The inverse of any quaternion is the conjugate divided by the norm. The details of such a calculation scare me (really, what is specifically done about the norm of a differential operator?). So I like it more in theory than in practice.
But what about spinors and gamma matrices and all that jazz? It has been my experience that with some effort, an alternative can be found. In the case of gamma matrices, quaternion triple products can be used to make 16 matrices that appear to do the job of the gamma matrices. The gamma matrices are a group, and the quaternion collection is not that group. As is common in these translations from standard techniques to quaternions-only, there is a half twist along the way. I don't think there is a right and wrong here, just the tensor status quo and the quaternion-only path.
Doing actual calculations with the Klein-Gordon equation is very difficult math. The 4-square approach may well involve new methods since there are now four equations in play. Such a research effort will always be beyond my limited reach.
[End wilder speculations]
What about other equations in quantum mechanics, such as the Schrödinger equation? In the name of consistency, the same logic must apply. Instead of the 2 before the mixed derivative term in the 4-square of the Klein-Gordon equation, there will be unity. There will also be a pure spatial derivative of the wave function.
Changing accounting systems faces a huge wall of resistance, even classically. In classical physics, one can go and work on the energy of a system. Then you can deal with momentum. With the quaternion accounting system, energy is in one slot and momentum sits in the next three doors. One feature is that solving a problem for energy means what happens with momentum is the next three terms.
Even the venerable approach using Lagrangians would have to change. Here I can point out a concrete benefit. The Lagrange density used to derived the Maxwell source equations is the magnetic field squared minus the electric field squared. If one reverses time, not a thing changes about that quantity. This is one of the ways to view the deep issue of the "problem of time". The Maxwell source equations cannot care if time reverses. Odd, deeply odd, until you realize that the Poynting vector sits right next door to this difference of squares. The Poynting vector does flip its direction under time reversal. I had enough trouble learning the basics of the calculus of variations to know I will not be able to handle having to play with the Poynting vector at the same time.
A change from tensor based calculations to quaternions is not going to happen in my lifetime. Nor will it happen in my daughter's time. Unless… unless someone with real physics chops start kicking the tires of the quaternion gravity proposal. All the good boys and girls will get their jobs trying to figure out how to bridge the divide between general relativity and quantum mechanics. If the past is a reliable guide, they will fail. Every. Last. One. For decades. The history of physics is harsh on this subject.
By the quaternion gravity proposal, the real problem involves how we calculate the intervals between events. That has two theories: special relativity the stuff of algebra and general relativity, a nonlinear field theory. Calculating the interval between two events should depend on one form of math. Hopefully it is the simpler one. If so, the other one would be wrong in the traditional scientific sense: useful in its time but no longer used. Simple Einstein beats nonlinear Einstein using quaternions instead of the tensors with their Einstein conventions that toss information under the bus.
Quaternion Gravity Resources: From simple to harder...
http://bit.ly/qg_sketch - Click on the pdf. Only 2 pages of work using pencil, like the old days
http://bit.ly/vp-qg - Get the big piture with fun animations I made with my daughter. Watch the "page-casts" to really get the idea. Use the arrows to go through the site in logical order.
http://bit.ly/vp-qg_talk - A 26 minute video on the subject with lots of math
http://bit.ly/qg_paper - A paper I submitted to a journal (still waiting for the reviewers)
http://quaternions.com - The mother ship
Recent blogs here:
Space-times-time Invariance as Gravity, Part A: the Proposal
Comments