Relativistic quantum field theory does not apply to everyday life. It doesn't apply to one beam circling the Large Hadron Collider (LHC). When two beams traveling in opposite directions smash together, that is when the crazy magic of relativistic quantum field theory dominates. In order to calculate the odds of scattering events, the sum of all possible histories must be accounted for. If one figures out the odds of an electron going forward in time to interact, then its antiparticle the positron going backward in time must also be added in. There is so much energy in such a small space-time that everything that can happen happens.
There are also rules about all the things that cannot happen. If you get lucky(?) enough to take a graduate level class on relativistic quantum field theory as I have, then you may do a few calculations to two loops (not that I could do those today). Anything beyond that is done by computers because the number of permutations explodes with each new loop. This is why having a small coupling constant is a good thing in perturbation theory because the series converges quickly. The fact that the detection teams at the LHC can keep supercomputers busy for months at a time with calculations designed to spot a new particle is to my eye the most impressive symphony of applied mathematics done by man.
In this blog I will share my insight into one of the pieces of math machinery used in relativistic quantum field theory calculations: the set of 16 gamma matrices. I will provide a sketch of where they come from, which is to say they scramble data in a systematic and crazy way. While I never can recall an exact gamma matrix, the quaternion approach is easy to remember. Mastering gamma matrices is an obscure art. I believe I can explain the quaternion method to almost anyone with an interest in physics.
A core equation for relativistic quantum field theory can almost be guessed as was done in the 20s first by Schrödinger. It should have second order time derivatives minus second order spatial derivatives, and a term with mass.
That is the right answer, known as the Klein-Gordon equation. Since it is my blog, I will show you how I like to derive almost-the-same-thing-but-DEFINITELY-NOT using quaternions. Quaternions often have this flaw. I find it endearing, others hear fingernails on a blackboard. I mark the text so you can skip it if you'd like.
< START quaternion KG-ish derivation>
Start with the energy-momentum 4-vector:
Square it:
The first term is invariant under a Lorentz transformation. Everyone uses it. Although the EP term is well-formed (it is composed of quantities we know how to measure), I don't know of anywhere it is used. In a situation where energy and momentum are conserved, then the product is conserved. Simple, well-defined omissions in the canon of physics strikes me as a very bad thing. It transforms just like gamma^2 beta, not simple like an invariant, but well-defined.
Substitute real operators for energy and momentum acting on a wave function. Quaternions already have imaginary numbers baked in so there is no need to include i.
This is where someone may point out that I got a sign wrong. Bring the squared m to the other side and the time derivative and mass squared term have different signs. For the Klein-Gordon equation, they have the same sign. The omission of the factors of i in the operator definition was the cause. I promised I was not going to derive the Klein-Gordon equation, so I didn't.
The final step in my approach is to make the equation dimensionless. Instead of using a subtraction to bring the mass over, I use it as a normalizing factor which makes the entire expression dimensionless:
This has every operator that appears in the Klein-Gordon equation. It is not that equation for several reasons. First there is a sign difference. Second, there are extra terms. Those terms arose in the second step, where the energy-momentum 4-vector was squared. My preference for a dimensionless expression means that it will produce the same numerical results no matter what arbitrary choices for units are made by experimenters.
It is also worth noting that the wave function used here is for a spin-0 scalar field. If one uses a 4-potential instead, one gets a spin-1 field and the Proca action. You may be able to spot the Maxwell equations in the Lorenz gauge if the mass is zero (but keep the mass m on the right hand side in that case).
The energy-momentum term looks well-defined. Could there be a benefit?
If the field equation has a gauge symmetry, that creates a technical problem. Roughly, we need to invert a field equation to generate the propagator used in quantum field equations. When there is a gauge symmetry, one needs to pick a gauge, then the propagator can be defined. With this expression, everything can be inverted because everything is part of the same division algebra. Even if there is a gauge symmetry, those other terms are not going to be zero. Can I back up that hope with a calculation? Nope, darn it. It will take someone 75 times smarter than I ("But Doug, 75 times zero is still zero." - a good math joke, but at least I thought of it first).
< END quaternion KG-ish derivation>
The big take away message is that the "obvious guess" for a second order differential equation is worthy of study. Is there a first order differential equation that is every bit as relativistic for quantum field theory?
[note: for those that hope for a more precise discussion that I can ever provide, I spent quite a bit of time reading and rereading the linked page.
Imagine, roughly, the square root of Klein-Gordon. That is what Dirac found. There must be a time derivative, a space derivative, a mass, and a wave function, but how can a first order differential equation be as rich as a second order one? Dirac worked his magic using a Clifford algebra, Cl(1,3)(R) symbolized by the gamma below:
A casual technical reader of this blog might see this and think the contraction of a contravariant (upper index) gamma with a covariant (lower index) derivative leads to a Lorentz invariant scalar. Actually, it's complicated. The gamma is a 4x4 matrix populated with constants. The result of this contraction are 4 differential equations. This also means we need to use a column for the wave function. What does it mean - physically - to go from one wave function to 4? Nothing, it is a different mathematical representation of the same physical situation. I know I should not worry about that switch, but I do.
A bit more verbose expression:
{original eq. which has a sign error)
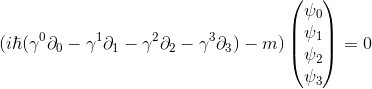
Corrected eq because this is just the sum, no metric is involved (see David's comment below)
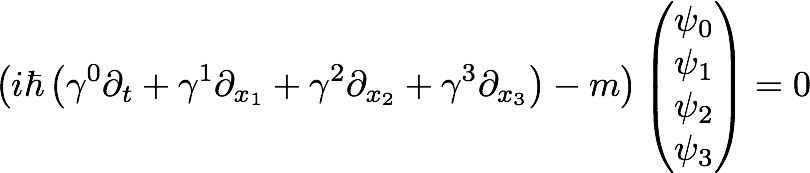
It is a zoo of gamma matrices that I have trouble keeping track of. There are a variety of identities one needs to prove. There are 4 gamma matrices, but don't forget about the fifth one. The fifth one doesn't belong in the Clifford algebra, but is useful for studying helicity. But to have a complete set, meaning that any constant 4x4 matrix can be represented by a linear combination of these matrices, then that complete set has 16 Dirac matrices.
I spent more than an hour writing that last paragraph, reading and rereading descriptions of the gamma/Dirac matrices, trying not to get confused about all the relationships. I have done that in the past too, but it still feels like too much math for me to keep track of.
So I am going back to the quaternions, and more importantly, physics.
To describe the atom smashing in bowels of the LHC, we need all possible histories.
That is the physics.
Start simple:
This is the couch potato transformation - nothing happens. That I understand (and the same thing does happen with gamma matrices).
Readers may quickly guess that I could multiply on the left by one of 4 basis vectors, and do the same on the right, for a total of 16 possibilities. Would that magically make up the complete set of 16 Dirac matrices that can represent any constant 4x4 matrix?
This was not my idea. As the owner of quaternions.com, I get papers sent to me as an "internet authority" on the subject. The paper was titled: "Dirac matrices using quaternions" by J. López-Bonilla and L. Rosales-Roldán. In hindsight, I should have question the paper based on the title alone. The Dirac matrices are the Clifford algebra CL(1,3) while quaternions are CL(0, 2). The two are never going to be the same.
One of the many subjects I have not studied in math is all the meanings of "the same", or more technically, morphisms. I have heard of the variety of them (iso, endo, auto, …), but have trouble getting them right. With considerable aid from David Halliday, I did figure out how exactly to go from the map suggested in the paper to the gamma matrices. It requires 5 extra factors of i.
Like the Klein-Gordon equation, the quaternions get the signs and factors of i wrong. We know the conventional Klein-Gordon equation and gamma matrices work together to do useful calculations. It is merely a belief on my part based on the ability to construct the map above that the quaternion not-KG and quaternion-triple-permutation-product-that's-not-gamma could be used in relativistic quantum field theory calculations. I work in too much isolation to work with someone on a demo calculation to give it a thumbs up or down.
From now on, I will assume that there is a way to use quaternions, odd sign conventions and all, to do useful calculations.
Let's work through the four "quaternion gamma's" to see what happens. First off is gamma zero:
My first response to this is simple: this is crazy complicated. Well, it should be to keep supercomputers busy for months on end. But that was an over-reaction. The source equations for the Maxwell equations in the Lorenz gauge in this pedantic format looks like so:
This of course is second order instead of first order, yet there is a clean organization of terms. No wonder light is easier to deal with than electrons.
There are 3 other gammas. Is anything important accomplished by doing them? No, the story is the same, only the signs and locations of terms varies (each of the 16 terms has to be somewhere, just somewhere different). Yet I will do the work because people learn through repetition, so here I go again with gamma 1:
Things stuck out when I did this calculation. When filling in the 0-3's at the end, I used the same LaTeX code as gamma 0, but traded 3's for 0's and 1's for 2's. The final line felt particularly odd, but that is the way the partial derivatives get all scrambled up.
Note: this really is a Sudoku puzzle. I checked for one partial of each of the four times, one phi in each row or column. Doing that check in the first draft indicated an error (two psi 0's in one line).
On to gamma 2!
This was similar to the last one, only some signs were changed. Anything with a partial of zero or two flipped signs. One more to go…
This time the signs stayed in the same places, but there was a swap of 0 for 1 and 2 for 3.
Nature has the capacity to keep track of this level of detailed variation, although I do not. I did notice that all four equations had one term with three minus signs, one with three positive signs, and two with one minus.
Scrambled Eqs
Light is comparatively simple: the same operator acting separately on one part of the potential at a time. The equations for matter look like they are the light equations that are systematically scrambled. I like that result because we know photons interact in many ways with matter.
A core difference between bosons and fermions is that for bosons, it takes the expected 2 pi rotation to get back to the starting place. Fermions take twice as much rotation. Sometimes this 2x requirement is presented as an impossible thing to understand, part of the magic of quantum mechanics. Actually, it happens for any cup you put in your hand. Sure, if you sit on a bar stool and spin around, it only takes 2 pi rotations. You and the cup together are free. But try to do the same where you don't move but the cup does. After 2 pi rotations, your hand and arm are not back where they started. That is due to the complications your shoulders create. When I look at the equations for Maxwell in the Lorenz gauge, they look like they are free to return after 2 pi rotations. The "quaternion Dirac" equations look like the signs will get all tangled up. Go around twice and two sign changes do make a positive.
Caveats, Caveats
I admitted I cannot do a calculation with any of the equations presented. If you choose to look at this blog as a silly game of quaternion gamesmanship, I can accept that position. When working exclusively in four dimensions as happens with the Klein-Gordon and Dirac equations, I could not justify avoiding a division algebra as it is manifestly a more powerful math tool. Granted, history is so on the side of tensors. If you were so motivated, I do think all references to quaternions could be deleted from this post, but a core message - the Maxwell equations in the Lorenz gauge is neatly separated, while the Dirac equation mixes things up - remains.
Why do only 4 of the 16 gamma matrices (mine or the standard set) get used? My guess would be that a different set of four could be used, but that is only a speculation. There may well be redundancy with the full 16.
The subject of helicity was not brought up. That might be fun to explore in a different blog. That process uses one plus or minus the non-CL(1,3) gamma 5. That is a big topic, this blog is long enough. I hope you see new relationships between the equations for light and matter.




Comments