In Part A, the core idea behind the space-times-time invariance as gravity was detailed. When one treats events as a 4-vector, the contraction of that 4-vector generates one number. When one treats events as quaternions, the square of a quaternion generates 4 numbers. If for two observers, the first number in the square is identical while the other three (I call space-times-time) are different, then the two observers are moving at a constant velocity relative to each other. The space-times-time proposal is exploring the case where the observers disagree about the interval, but have the same space-times-time.


When I discussed this proposal with a physicists in June, he mentioned I needed to write out the equations of motion. For a field theory, the equations of motion are generated by varying the Lagrange density with respect to position and velocity and finding an extremum. The space-times-time invariance proposal does not have a Lagrangian. Bummer. I spent the summer worrying about the math underpinnings of quaternions, but knew I had to return to the equations of motion in the Fall.


For the space-times-time invariance proposal, the invariance applies to all quaternion expressions.


1. Start with momentum-energy written in spherical coordinates:

EP.png


2. Work in the plane with θ = π/2 , and dθ/dτ =0 :

EP_in_a_plane.png


3. In a space-time with a gravitational mass, the product of the time term and radial term must be invariant. Use an exponential function because that function is consistent with experimental tests of gravity and the invariance requirement of this proposal:

EP_in_a_plane_w_gravity.png

Technical note: I am using Schwarzschild spherical coordinates. This means that space is not being treated isotrophically. Instead, the changes in space due to gravity are all radial. This is a standard thing to do.

4. Square 3:

EP_squared.png


Notice that the radial space-times-time term is the same no matter where measurements are made in a gravitational field. That is the idea behind the space-times-time invariance proposal.


5. Focus on the first term of the square, rearranging to remove the exponential factor from the radial term:

V2_w_exp.png


6. Equation 3 has no dependence on either time t or angle φ . This indicates both energy E and angular momentum L are conserved. Use equation 3 with these conserved quantities to make substitutions for equation 5:


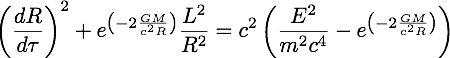
7. Presume the exponent on the exponential is small enough that only the first order terms are relevant. Keep the constants on the right, all other terms on the left:


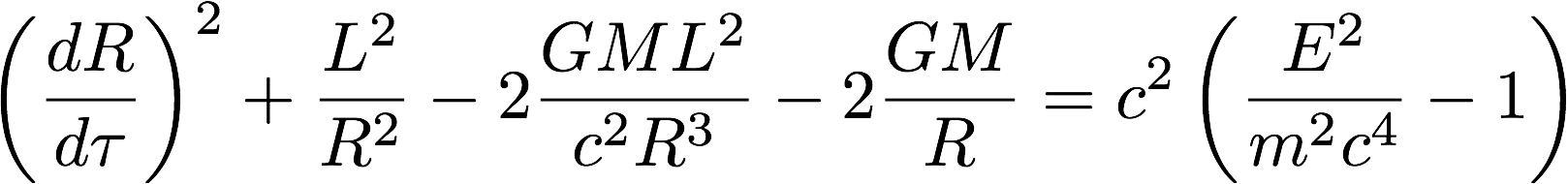
This equation has the same form as the equations of motion for the Schwarzschild solution of general relativity. The precision of the perihelion of Mercury calculation uses this form (it is step 7 of 24 in a blog I wrote that goes into that calculation with excessive detail).