Bernhard Meirose is a researcher at Stockholm University and associate professor (docent) at Lund University. He has a doctoral degree from the Federal University of Rio de Janeiro, Brazil, and has previously worked as a postdoctoral researcher at the European Organization for Nuclear Research (CERN) and at Freiburg University, Germany. He was also a research scientist and adjunct professor with the University of Texas at Dallas (USA). His research focuses on experimental and phenomenological particle physics.
Bernhard was a member of the ATLAS Collaboration from 2007 until 2021, having worked with diverse subjects within the area, including physics analysis, detector and Monte Carlo simulation, as well as algorithms for reconstruction and identification of particles. He coordinated the searches for prompt dark photons between 2014 and 2018. In 2014, he was one of the co-proposers of the NNBAR experiment at the European Spallation Source and was appointed detector simulation coordinator of the experiment in January 2021.
Last November I had the luck to bump into Bernhard at the KLM lounge of the Amsterdam airport, where I was killing time waiting for my flight. I did not know him, but when I saw his laptop screen showing a slide on the GEANT4 program I stepped forward, asking "Hi, are you a particle physicist?" He raised his eyes from the screen, looked at me, and replied "Yes, are you Tommaso?". Turns out Bernhard reads my blog. An interesting discussion ensued, at the end of which we agreed he would write for this column about his very interesting research.
The text below is what he offered. Thank you Bernhard!
-----
Whether or not you are a professional scientist, you have most probably heard about neutrons. All atoms in nature, with the exception of the most common isotope of hydrogen, contain neutrons. A curious fact about them is that a free neutron is unstable and spontaneously decays to a proton, an electron, and an antineutrino in just under 15 minutes on average. It has long been proposed that a free neutron may also be able to do something very special before decaying - converting to antimatter (an antineutron). We're now able to design a high precision experiment (HIBEAM/NNBAR) to look for this. This is an experiment with a unique observable and capability that forms part of a complementary worldwide program of experiments, each turning over its own rock to look for something called baryon number violation. Any observation of this would of a fundamental significance akin to the discovery of the Higgs particle. Our experiment comes with an improvement in sensitivity 1000 times greater than previous achieved. Such a leap in sensitivity is rare in particle physics experiments.
To understand this business of baryon number violation, it is useful to think about protons. We know that free neutrons decay. What about protons? Protons could decay, for example, into a neutral pion and a positron (a positively charged twin of the electron):
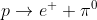, as shown in Figure 1. There is only one problem with that. Nobody has ever seen a proton decaying into anything (you can see for yourself in Wikipedia that "proton decay" is on the list of the most important unsolved problems in physics). So, despite years of experimental search, nobody has ever observed proton decay. According to the current best limit coming from the Super-Kamiokande water Cherenkov radiation detector in Japan, if protons decay, they must do this after 10^34 years. Given that the estimated age of the Universe is of the order of 10^10 years, this result was obtained by observing a large number of protons over a measurable period of time and checking that, indeed, no protons ever decayed. OK, so if protons do not decay, what mechanism is preventing them from doing so?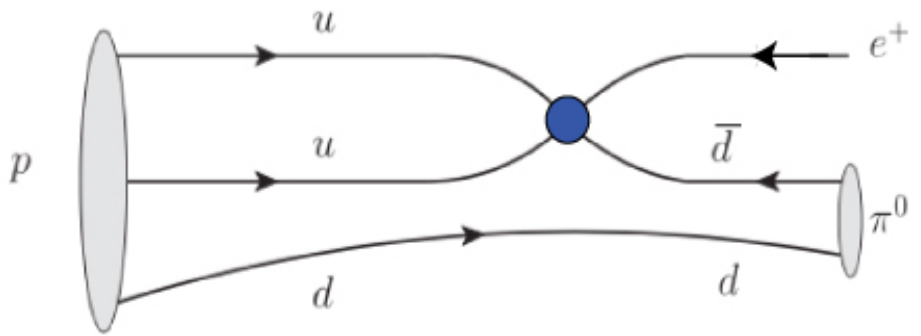
Figure 1. A free proton decaying into a positron and a neutral pion (long sought but never observed).
In the Standard Model of particle physics we "explain" this by saying that protons do not decay because they must conserve a quantity called "baryon number" that was first postulated in 1929 by the German theoretical physicist and mathematician Hermann Weyl in order to "explain" the non-observation of proton decay. Baryon is the name given to any composite state with three quarks. Since the proton is the lightest baryon, with one unit of baryonic number (B = 1), it cannot decay into anything else. The decay I mentioned earlier (neutral pion and a positron) would violate the total baryon number, because the final baryon number of the system would be zero, given that neither pions nor positrons are baryons. I hope you caught my cynicism in using "explain" in quotation marks because this has not really explained anything (we could have called it "Smurf number" and ended up at the same conclusion). Whether or not I or anyone else like it, however, baryon number conservation stuck and no experiment has ever observed any violation of it. Were it only for the mere knowledge on proton longevity I'm not sure I could care that much. However, the concept of baryon number violation is at the heart of some fundamental open questions in modern physics.
An outstanding problem in physics is explanation of the observed imbalance between matter (baryons, B = 1) and antimatter (antibaryons, B = - 1) of the Universe. The problem is that matter and antimatter annihilate producing photons (the particles light is made of) and, according to the Big Bang theory, matter and antimatter should have been created in equal amounts. But this is not what we observe - the Universe is not made of pure light, and there are more baryons than antibaryons out there. In order to explain the mystery, in 1967, the Soviet physicist Andrei Sakharov proposed three conditions to explain the process which lead to baryonic matter dominance over antibaryonic matter, which is commonly known as "baryogenesis". For the curious, you are welcome to look all the conditions up, but I will limit myself to say that baryon number violation is one of these conditions - in other words, the condition is necessary (although not sufficient) to explain baryogenesis.
What about the Standard Model of particle physics ? The Standard Model is built on so-called symmetries which give conservation laws. However, not all conservation laws are made equal. For example, the Standard Model robustly protects electric charge conservation - it corresponds to a gauge symmetry which is one of the engines of that theory. Baryon number conservation arises due to a so-called accident symmetry. It wasn't explicitly stuck in as a guiding principle of the model but it appears when the model is assembled. The Great Game of physicists is to think beyond the Standard Model. Although new theories must keep the highly successful engine (theorists don't want to predict electric charge non-conservation), baryon number conservation tends to vanish when the Standard Model is extended.
Given everything that baryon number violation could explain and demonstrate the stakes are high. Moreover, in view of the fact that the original motivation for baryon number conservation postulation was pretty ad hoc , I am not holding my breath it will hold. In fact I am betting it will one day be violated (if I'm lucky, during my lifetime). And the best experiment to cleanly check whether baryon number is violated is not in proton decay experiments, but in something called a free neutron oscillation. With "cleanly" I mean, a process where only baryon number is violated. In proton decay experiments, baryon number is violated, but the problem is that lepton number (another additive quantum number just like baryon number, but for leptons, like electrons and muons) is also violated (since there is no lepton in the initial state but there is a lepton, the positron, in the final state). But what exactly is a neutron oscillation and how may we detect it?
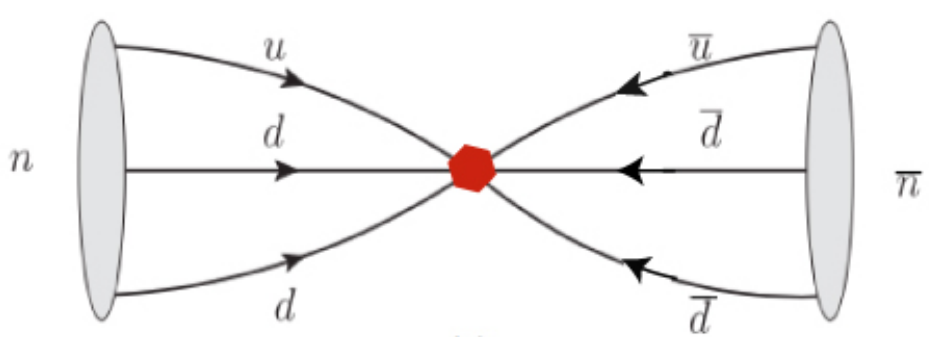
Figure 2. A neutron spontaneously transforming into an antineutron.
In a neutron oscillation, a neutron (baryon) can spontaneously transform to an antineutron (antibaryon), as shown in Figure 2, and this can happen, in principle, back and forth, hence it can oscillate between the two states. There are no other quantum numbers involved so only baryon number is violated. In order to measure the process, a large number of neutrons must be allowed to fly freely for as long as possible - this is to increase the chance of at least one neutron transforming to an antineutron.
Just like when you play the lottery, where you increase the chance of winning by buying more tickets, you increase the chance of observing a rare process (if it exists, it must be at least rare, otherwise it would already have been observed) by increasing the number of particles. Moreover, by observing each neutron for as long as you can, you increase the chances of seeing the process, so you want not only free flying neutrons, but slow flying neutrons.
The perfect conditions for this measurement surged with the construction of the European Spallation Source in Lund, Sweden, shown in Figure 3. The facility is under construction and when ready it will be the most powerful neutron source in the world, meaning the number of neutrons available will be unprecedented. Furthermore, a long fly path of 200 m is available as well as novel moderator technology (moderators slow down fast neutrons). The combination of all these advancements, turn a free neutron oscillation experiment at the ESS a thousand times more sensitive to observe a neutron oscillation compared to the last experiment with free neutrons that did this same search, in the 1990's at the Institute Laue-Langevin, in France. This unique scientific opportunity led to the formation of the NNBAR international collaboration. The collaboration proposes to build the experiment at the European Spallation Source beginning the data taking around 2030.
Figure 3. Aerial view over ESS site January 2021.
An important point to add is that, in order to observe an antineutron one needs to be able to measure its annihilation products, so one needs to put a suitable material on the path of the neutrons for which there is a very large chance of antineutron annihilation, in case a neutron to antineutron transformation occurs. This is accomplished with carbon, where it is expected an antineutron would annihilate practically 100% of the time. When an antineutron annihilates with one of the neutrons from carbon, it will produce several pions, which must be caught by a detector surrounding it. The evidence would be clean and striking - charged and neutron pions coming from the same origin (vertex) and by summing up the masses and energies of all pions they should add up to two neutron masses (one for the neutron in the carbon, the other for the antineutron). The scheme of the experiment can be seen in Figure 4.
Figure 4, A schematic view of the free neutron-antineutron oscillation experiment at the European Spallation Source.
And what would the observation of baryon number mean? Besides fulfilling one of Sakharov conditions and by it shedding light into one of the most important problems in modern cosmology, the observation of baryon number violation in free neutron oscillations would be the first evidence of non-Standard Model physics outside the neutrino sector (the original formulation of the Standard Model contained neutrinos with zero mass, which we know for a fact not to be longer true - however this was hardly a prediction, it simply accommodated what was known about neutrinos back then and extending the model to accommodate massive neutrinos requires minor adjustments).
What this means is that observation of neutron to antineutron requires the existence of a new interaction, mediated by a new particle or particles! Something must do the exchange that allows the transformation to happen. Maybe it would be something unexpected or perhaps it would have been predicted among the tons of beyond Standard Model theories out there. However, the really important fact that is that we would have confirmed for the first time experimentally, without any shed of doubt that the Standard Model is falsified.
If you follow anything about particle physics you must have heard ad nauseam that the Standard Model is incomplete, which I also believe it to be true. However the incompleteness generally refers to things the Standard Model has nothing to say about, rather than actual tensions between theory and experiment. Not even dark matter can be claimed as definitive that such tension exists since the evidence, albeit very compelling, is all astronomical, not microscopical. So, neutron to antineutron observation would very clearly represent a significant advancement in our understanding of fundamental theory.
Further reading:
- https://nnbar.eu/
- https://inspirehep.net/literature/1800401
Comments