No, unfortunately not yet the discovery of the century. Still, the new particle found by CMS in its 2011 dataset is a very important piece of the puzzle of low-energy spectroscopy. Here "low" should be taken with a pinch of salt: the new particle, an excited state of the Ξ_b series, has a mass only slightly lower than six GeV, and is thus "heavy" if compared to most other hadrons.

The CMS experiment is one of the two omni-purpose detectors at the Large Hadron Collider (LHC), the "end-of-the-world" machine colliding protons at the CERN laboratories near Geneva, at the border between Switzerland and France. It is operated by a multi-national collaboration of over 3000 physicists, and is now investigating the large datasets of 7-TeV collisions collected in 2011, as well as giving a first look at the new 8-TeV ones that are being produced as we speak by the LHC. The LHC plan this year is to triple the data delivered to the experiments last year, which - combined with the higher centre-of-mass energy - should quite significantly increase the discovery reach of ATLAS and CMS for heavy (this time, real-heavy) new particles in the multi-TeV regime.

So what is this new particle that has been observed for the first time in CMS ? It is a bound state of a bottom quark and two lighter quarks, a (bsu) combination; and to be precise, an excited state of these three quarks. Just as you can have a excited hydrogen atom when the single electron orbiting around the proton carries more energy than it does in its fundamental state, and is ready to let this extra energy go in the form of a quantum of light, the quarks in the Ξ*_b (the asterisk indicates the excited nature of the baryon) carry more energy than in the fundamental Ξ_b hadron, and this allows the new hadron to spend the extra energy by decaying via the strong interaction into a more "fundamental" state -a negative Ξ_b - with the emission of a light positive pion, a bound state of a up-antidown quark pair.

Note that the above analogy is only partly justified; it would have been better to use excited nucleus instead than a whole atom, but I am not sure how many of you are familiar with that concept. Plus, the pion is not the quantum of strong interactions! It was mistakenly taken as such by Yukawa only seventy years ago, shortly after its discovery -it fit the bill of the then mysterious force binding nuclei together quite well, just by accident. Nowadays we now know better; still, the de-excitation mechanism produced by quantum chromodynamics is not altogether that different from the one of the excited hydrogen atom.

What happens to the decay products of the excited Ξ*_b is crucial in order to allow CMS to observe the process. The Ξ_b, a particle first observed by the Tevatron experiments, decays by weak interaction into a J/ψ and a negative Ξ baryon (a regular one, containing no b-quarks and so a dss quark combination) when the b-quark turns into a charm and another anticharm quark "pops into existence" together with a strange one. A quark-line diagram of the decay chain will clarify how the reaction takes place:



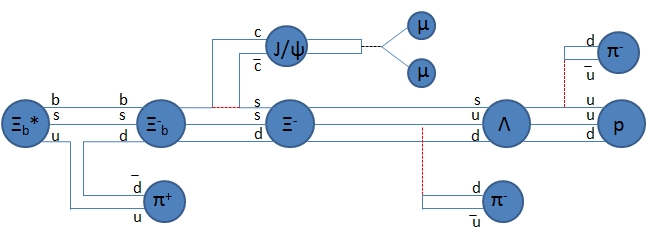
The diagram should be read from left to right. The bigger balls are the baryons: a fundamental rule of particle physics dictates that the number of baryons (eventually subtracted of the number of anti-baryons) remains the same in whatsoever reaction one considers. So we have a big ball to the left, and we need to continue having a big ball throughout as the reaction develops, until we end up with a proton, the lightest big ball, and thus a perfectly stable baryon which cannot turn into anything else. Fortunately so, since otherwise we ourselves would also live a shorter and more radiating life than we do: we are made of protons (and neutrons, which are stable within nuclei; but that's another story).

The continuous lines in the diagram (except those of muons) show the propagation of quarks. At the very left we start with a b, a s, and a u quark in the Ξ*_b: three lines from top to bottom. The u quark line soon diverges to become part of a positive pion (the leftmost smaller ball). To make a positive pion the u quark must bind with a anti-down one, which is the other line. That line is connected with the quark line which takes the place of the original up quark in the baryon: this down-antidown pair has "popped into existence" thanks to the strong interaction which de-excites the Ξ*_b into a Ξ_b^-, which is now made up of a (bsd) quark triplet.

But soon, the b quark decays by weak interaction (with the emission of a negative W boson, shown by a red dashed line). The b thus turns into a charm, which becomes part of a J/ψ meson. The J/ψ is a bound state of a charm-anticharm pair, so the anti-charm must be the result of the negative W disintegration. Together with it, a strange quark is created, so that the resulting baryon is now a Ξ^-, a particle made now by a (ssd) combination. In other words, the decay of the Ξ_b^- occurs by the conversion of a b-quark into a charm quark; but it is not the latter which takes the place of the b; rather, it is the strange quark popped into existence by the W boson.

Next, following left to right the chain of events, it is the turn of the Ξ^- to decay, again by weak interaction (emission of another W^- boson, which materializes a negative pion (down-antiup quark pair)): the result is a Lambda baryon, which is a (usd) combination. Finally, the Λ itself decays, when the last strange quark remaining turns into a up quark emitting a further W^- boson, which finally creates a negative pion (rightmost smaller ball), a down-antiup combination.

Quite a reaction, isn't it ? And we have not even mentioned that the J/ψ meson itself decays, by electromagnetic interaction, yielding a muon pair (small balls). Experimentally, the whole chain of decays is reconstructed "right to left": first, proton-pion pairs are combined into lambda candidates; then a negative track is combined with these to form a Ξ^- candidate; the latter is then combined with the two muons making up the signal of J/ψ decay; and finally a further positive track is combined with the system. In the hypothesis that the whole set of final state particles observed -three pions, a proton, and two muons- come from the decay of a single body, the combined invariant mass of these particles must equal the mass of the decaying new particle.

Experimentally, what we do to is a slightly different thing than the plain attempt at measuring the mass of the new particle straight away. Other experiments have measured with exceptional precision the mass of the J/ψ, and also the mass of the Ξ_b^- is well known: so it makes sense to compute the mass difference between the total system of final state bodies and the combined mass of the J/ψ and Ξ_b^-, added by the mass of the first pion: this difference has a much better resolution than the total mass of the whole set of particles, and it still has a single value if the reaction is indeed the decay of an excited Ξ*_b state. So by studying the distribution of the mass difference M(J/ψ Ξ_b^- π) - M(J/ψ Ξ_b^-) - M(π) the signal peak, if any, will stand out much more clearly on top of a flat background due to a random combination of real particle signals (the J/ψ and the Ξ_b^-) and a pion which happened to be passing nearby.

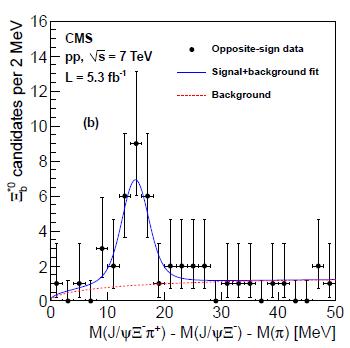The analysis that selects the data (obtained by a trigger selecting J/ψ decays to muon pairs, a quite effective selection strategy for b-quark-enriched datasets) is quite complex and I cannot describe it in detail. Let us therefore just look at the mass difference spectrum. It is shown on the right.

As you can see, there is a clear peak in the data for mass differences close to zero. This is due to the fact that the excited baryon has little extra energy left to impart as momentum to its decay products: most of it just goes into the creation of the fundamental Ξ state and the pion. The red dashed line shows the background shape one would expect from combinatorial backgrounds, and the blue line is the signal plus background fit.

The significance of this signal has been studied with a number of advanced methods, and it is well in excess of five standard deviations even if one makes taxing assumptions about the range where the search has been performed and other effects. So it is safe to say that we are indeed looking at a real new particle signal. The mass of the new baryon can be computed to be 5945 MeV, with less-than-1-MeV uncertainties from the measurement and a 2.7 MeV uncertainty coming from the knowledge of other mass states! This peculiarity is due to the smart "mass difference" method, which relies on previous measurements to sharpen the mass resolution.

In conclusion, CMS has found a new baryon. A particle which is not a surprise -we know excited states of all hadrons exist; however, we still have a lot to learn about the details of these excitations, so the CMS measurement does constitute a true advancement of our knowledge.