Being an avid mineral collector, my house is full of specimens. They appear a bit everywhere in display cabinets and book shelves. Over the years I have collected over 300 pieces, plus a hundred gemstones, and I remember of course almost everything about each of them, from where I got them from, what is their origin, etcetera. But leaving things as they stand is a bit silly - if I had a heart attack and died, for instance, my family members would not know all these data, which would otherwise be useful if they decided to sell my collection, say.
The solution is obvious, and I finally found the time to implement it. I decided to create an excel spreadsheet with all the data I could collect, plus pictures, for each of my specimens, along with an estimated retail value. It took a while, but it's finally done. Things look very tidy now!
However, by cataloging every specimen, I realized that there were two or three for which I was not sure of the identity.
In one case it was a gemstone, the one shown in the picture below. A measurement of its weight with a precise scale gave the result of 0.412 grams (2.06 carats). Observation through a 20x loupe showed a few minor flaws, indicating it was a natural cut stone. But what was it?

There are many ways to determine the nature of a gemstone, which exploit the different physical and chemical properties that different crystallized substances exhibit. However, some of them are more invasive than others; e.g., one could determine what solvents attack the material, but this could leave nasty stains or corrosion on the stone's surface. Even trying to figure out the hardness of the substance by observing whether it scratches surfaces of other stones or whether it is scratched by them can be a bad idea, of course. The same goes for the study of the "streak", i.e. by observing the colour of the streak that the material leaves when swiped against a porous material.
Among non-invasive methods the two most used are the determination of the specific gravity of the crystal and of its refractive index. The latter is tricky and requires precise instruments to be carried out (I saw a couple on amazon on sale for about 300 bucks, forget it - I'd rather buy another fancy stone!), but the former is something you can achieve if you have a precise scale at home.
A digital scale with a precision of 0.001 grams costs about 20$, and indeed I purchased one a while ago, for the exact purpose of determining the precise weight of my gemstones. Today, though, I spent my time with some hardware to create the possibility of determining the specific gravity of the stone I wanted to assay.
How can you perform a specific gravity measurement? In general, specific gravity (or density) of a material is the ratio between the weight and the volume of an (homogeneous) object made up of it. Determining by size measurements and geometrical calculations the volume of a small object of complex shape, however, is nowhere near easy. It is much better to use an indirect method - and the simplest one was devised by Archimedes over 2400 years ago!
Archimedes observed that bodies immersed in water receive an upward push of strength equal to the weight of water they displace. Hence, if you weigh the object in air and in water, the latter measurement will tell you what is the weight of the water occupying its volume! The calculation goes as follows: if A is the weight in air, and B the weight in water, the density of the material of which the body is composed is A / (A-B). So e.g., if a body weighs three grams if you put it on the scale, and weights one gram when you weigh it in water, its density is 3/(3-1)=1.5, in grams per cubic centimeter units.
Below is the makeshift arrangement I came up with to determine the weight of my gemstones in water. You can see the digital scale, above which there is a "bridge" with a small water container on top. The bridge does not rest on the scale, but on the table underneath, through some adhesive ammortizers. Instead, the rather clumsy construction held by four red plastic supports ultimately rests, and transfers its weight (and the weight of stones placed on its central stone holder "spoon") on the scale dish.

The measurement procedure goes as follows: I first measure the gemstone weight alone, then move the scale under the bridge, put the red thingy on the dish, and weigh it without the stone, with the stone holder already immersed in the water. Then I add the stone to the stone holder, record the new weight, and now, since the stone is contributing to the total weight diminished by its upward Archimedes' pull, the weight of the stone in water can be determined as the difference of this last measurement and the previous one!
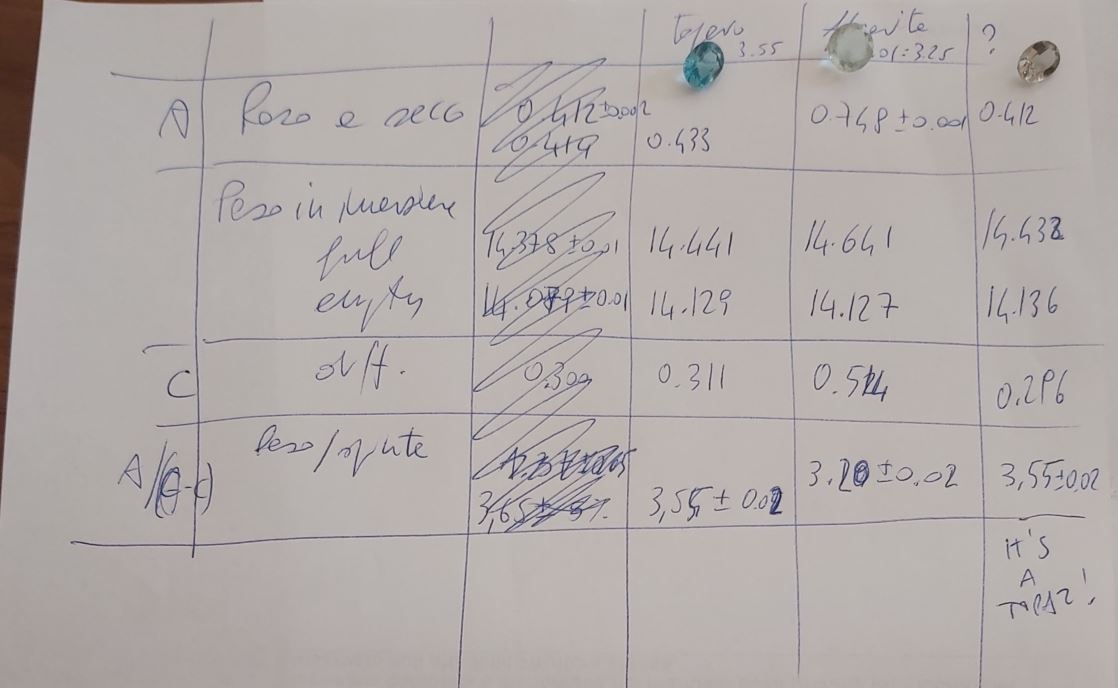
The page with scribblings shown above details the work of today. As you can see, I first used a couple of stones whose nature I was certain of: a 2.12 carat topaz and a 3.7 carat fluorite. Google says that the former has a specific gravity of 3.55 grams per cm^3, and the latter of 3.01:3.25, depending on the contaminants of the substance (fluorite has a variety of colours which are given by the inclusion of different substances, which affect its specific weight).
Let us run the calculation with the numbers I obtained for the first stone: I measured 0.433 grams for the weight in air, 1.4.441 - 14.129 = 0.312 grams for the weight in water, and so the density comes out to be D = 0.433/(0.433-0.312) = 3.579 +- 0.094 grams/cm^3. Bingo! It works! (In the scribblings above I estimated densities by calculating the ratio by heart, so it's slightly off from the real value; I later used a calculator to get three digits).
In the above calculation, the uncertainty I estimated comes from assessing as 0.002 grams the uncertainty in the various weight estimates. I will spare the calculation of error propagation, although it is by no means a difficult one; what matters, though, is that carrying that calculation out allows to observe that the technique used to determine the gemstone density is plagued by a significant uncertainty, as one has to appraise the small "upward push" which, for very small stones, can be really tiny.
The formula of the uncertainty is the following:
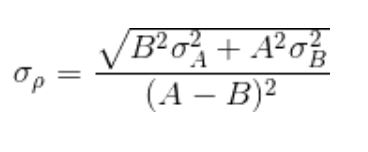
Above, σ(ρ) is the uncertainty in the density of an object weighing A grams in air and B grams in water.
That said, I ran the calculation with the numbers of the fluorite specimen, obtaining 0.748 grams in air and 0.514 grams in water, giving a density estimate of 3.197+-0.043 grams/cm^3: again, in very good agreement with expectations.
And now let us see what I got for my mysterious stone: its weight was of 0.412 grams; in water, however, this decreased to 0.296 grams. The density I computed was thus of 3.552+-0.097 grams/cm^3. It most certainly is also a topaz! Indeed, there are few stones with that specific weight, and in addition, the gem does look like a blueish variety of that stone.
In detail, the following stones have densities in the 3.4-3.7 grams /cm^3 range:
Vesuvianite 3.4
Epidote 3.4-3.5
Diamond 3.5 (I wish!)
Titanite 3.5
Topaz 3.55
Rhodonite 3.5-3.7
Spinel 3.5-4.0
Garnet 3.5-4.3
Kyanite 3.6
Chrysoberyl 3.7-3.8
All of them can be excluded for one reason or the other, except the topaz.
If you got this down reading this article, I feel compelled to give you more detail. One of the things any experimental physicist knows is that measurements are always affected with systematic uncertainties. Above, we only estimated statistical ones, by propagating them with a couple of partial derivatives. Systematic uncertainties are sometimes the dominant sources of uncertainty, so one always needs to consider all possible sources and try to estimate them.
In our setup, one should question the reproducibility of the measurement in several ways. First of all, when one plunges the stone in the water, the water level in the small container rises a bit. By raising up, a longer piece of stone holder gets dipped in the water, and that material also receives an upward push that was not present before. It is a small effect (I estimated it as of the order of a milligram or so) but a careful analysis should consider it.
In addition, a precise measurement should account for the density of air (air also pushes up, as does water!); in addition, water has a 1gr/cm^3 density only at a precise value of temperature (4 degrees Celsius), and if the temperature differs, the density also does, with systematic effects on the upward push.
I could jolly well go on, but I think my job is done here. If you have spare time and a digital scale, why don't you build your own density meter today ?





Comments