Now, I think all my colleagues would agree that explaining what is this quantity we call "anomalous magnetic moment of the muon" in layman terms is no joke; explaining even in handwaving fashion how the latest theoretical result has been cooked up is similarly quite a tall order. Fine - that's exactly what we do here: stand tall and wide above and away from normal outreach, and try to empower our readers instead than treating them like fifth-graders. Hence please take a comfortable chair and read on, unless you are a fifth-grader; while if you are a fifth-grader you don't need it, as you probably do not suffer from backache
The muon and you
The muon is an ephemeral subnuclear particle which does not exist in normal matter. A heavier replica of the electron, the muon can be produced in laboratory through energetic collisions where the involved kinetic energy of projectiles can be turned into its rest mass, which is about 200 times larger than that of the electron. The muon then decays in an average 2 millionths of a second, producing an electron and two neutrinos.
Despite the above, muons are with us all the time, as they get copiously produced as secondary products when interactions of energetic cosmic rays (mostly protons and light nuclei) with atoms of the upper Earth atmosphere produce pions and kaons, which then decay to those particles. These atmospheric muons rain down to the surface of the Earth in numbers of the order of 100 per square meter per second. So as you read this, a few energetic muons are crossing your brain every second, possibly activating some of your neurons by the released energy. Is that a source of apparently untriggered thoughts? Maybe. But I am divagating.
The muon anomaly
What is anomalous with the muon is that the muon, like the electron, possesses a quantity physicists call "spin". Spin can be loosely discussed as an analogue of the spin of a ball around its axis, but once you remember that elementary particles are point-like and thus there is no rotation and no axis, that picture becomes a bit less well defined. Regardless, a spinning electric charge (the muon is charged like the electron is) produces a magnetic field.
Through dedicated, high-complexity experiments which involve the production and storage of large amounts of muons in a circular accelerator, and the detection of their decays, we can measure the magnetic field of the muon. The last experiment which did so, with an accuracy much higher than predecessors, is the "g minus 2" experiment at the Brookhaven laboratories.
The reason why it is interesting to measure such an abstruse physical constant is that it is an abstruse physical constant. And, like abstruse physical constants tend to do, it can be predicted by abstruse theoretical calculations. To just give you a glimpse of how abstruse these calculations are, it suffices to show a graph of a small fraction of the Feynman graphs that theorists have to draw on their blackboards, and then individually turn into mindbogglingly complex formulas, computing their relative contribution to the quantity being estimated.
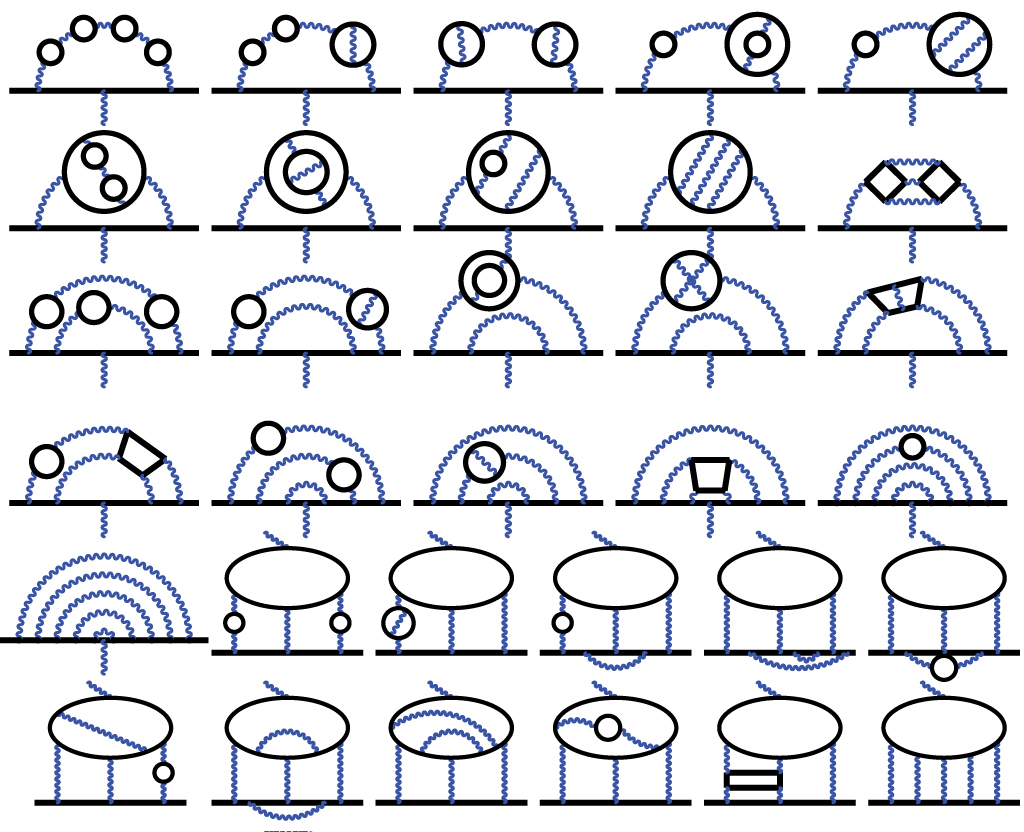
Each wiggle in the graph above is a photon, which can be emitted or absorbed when a muon walks around - photons, in fact, couple to electric charges no matter who is the owner, so they do this with muons as they do with electrons, or with any other body possessing electric charge. These graphs allow physicists to compute what magnetic moment should be possessed by the muon. That value, compared to experimental determinations, is at odds with them by almost 4 standard deviations, meaning that either somebody did a mistake somewhere, or that there is some new physical process that contributes to how much of a magnetic field the muon produces.
Lattice QCD
But there's another player in this game of theory versus experiment. In fact, some of the contributions to the calculation can be estimated by a very different technique than that based on Feynman diagrams. And these are crucially those which are the hardest to calculate precisely. In a different post last week I have discussed how a recently proposed new experiment, MUonE, can try to also attack the same problem; the issue is that these "hadronic contributions" are very difficult to evaluate.
Lattice QCD is a calculation of the effects of strong interactions that sidesteps some of their non-calculable features by "throwing the problem on the lattice": by formulating the quantum field theory as one based on a discrete grid of equally spaced spacetime points, calculations can be performed, sometimes with amazing precision. They require enormous CPU to be performed, but Moore's law has helped a lot in the past decades, so Lattice QCD is now on much more solid ground than it used to be.
In the recent preprint by Sz. Borsanyi et al. quoted above, a full blown calculation of QCD contributions to the muon magnetic moment is produced. And it results in an estimate which is in stark disagreement with previous determinations, and (suspiciously, some would say) instead in great agreement with the value one would guess if one had to bring theory and experiment to match perfectly! You can check this in the graph below.
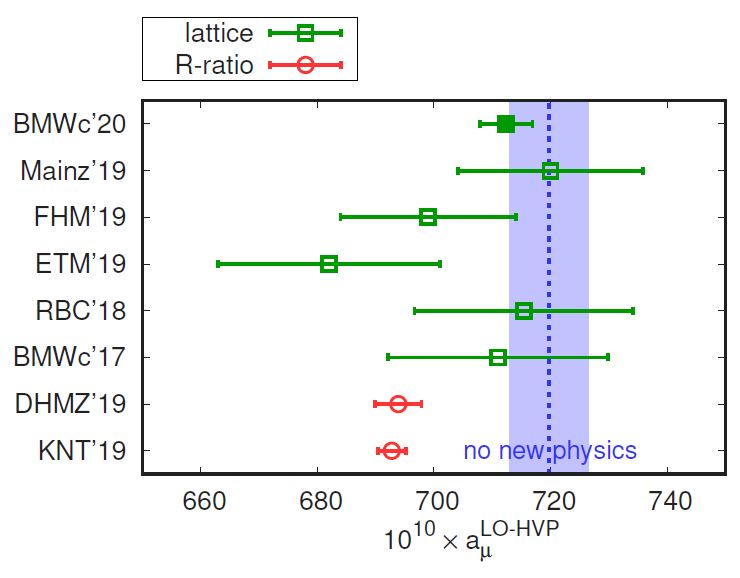
The result we are talking about is the one on the top row, which has a much smaller uncertainty (horizontal bars) than previous estimates based on lattice calculations. The current measurements of the parameter based on the more standard calculations are in red at the bottom, and they are seen to be wide away from the blue line, which is the value compatible with what the experiments are measuring.
If proven correct, the German-French-Hungarian-US-Japanese group of lattice QCD physicists will shatter one of the last few hopes that many particle physicists have clung to until now - i.e., that the muon anomaly would demonstrate the existence of new physics beyond the Standard Model. New particles circulating in quantum loops affecting the muon anomalous magnetic moment, in fact, could make themselves felt exactly by altering the value of that quantity. But if the quantity agrees with a calculation that ignores their contribution, there is no notitia criminis any more - there goes maybe the last clear hint in our possession that there be something out there to discover.
Is there still hope?
So, are you a disgruntled particle physicist, who wants one reason to hope? I will give you one. The result could be wrong. In fact, it is very hard to accept that both this last result and the previous calculations are both correct, and that their difference is due to some wild fluctuation of the respective uncertainties. So at the moment, that is until an independent group confirms the latest result, one has to decide where to place one's chips.
I do not possess the expertise to plunge into the detail of the calculation produced by the authors of the cited paper, in search for a mistake. What I can do, though, is to nit-pick. I thus paste below a graph taken from Fig.12 in the paper. This has relevance for the estimate of the muon anomaly, so I imagine it will be the culprit of discussions in the future.
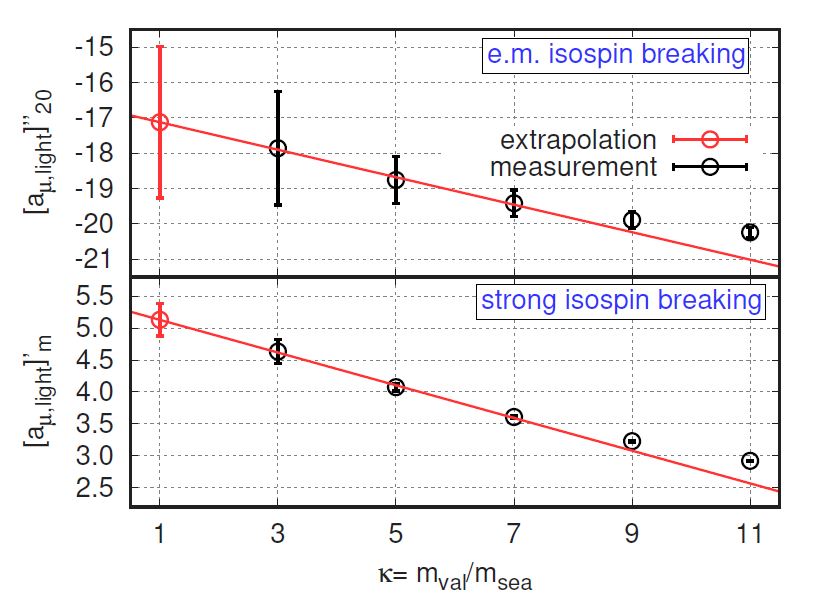
Authors use an extrapolation to estimate the value of two parameters affecting the muon anomaly correction. These are shown as points with red bars at the left of the two panels. The extrapolations are based on linear fits to the three closest points on the right. The abscissa is a ratio between assumed values of the mass of valence and sea quarks - you can happily ignore this bit, but the relevant thing is that when you extrapolate you should do so with the smallest level arm you can, and that is what authors do by taking the close points; but you should also use all the relevant information you have, unless you can prove that the extra one you left out is irrelevant or nocuous. And this is, to my understanding, not done in the article. [Disclaimer 1: I might be wrong, as I already explained I am not an expert and I have probably missed important information from my casual browsing of the article. Please correct me in the thread below if that is the case!]
So one might be left with the doubt that if the two points at higher mass ratio had been included in the extrapolation fit, the result would have been significantly different, lowering the two estimated contributions beyond the range of the quoted error bars on the extrapolated parameters. Now, in data analysis, any ad-hockery or non-pre-data-justified procedures must ALWAYS be regarded as suspicious. Plus, researchers are human being, and they (I mean we) too, like the rest of us (I mean you) fall sometimes prey to our desires. As the precise value extracted by this result is exactly the one that produces the highest impact in the field, one is justified in questioning every bit of its cooking with the strongest possible determination.
[Authors of the paper should excuse me if I seem to imply any sort of misconduct: my comment is absolutely general here, and it applies to any scientist.]
Whether this is a relevant information, however, remains obscure to me. Maybe some lattice QCD tourist-theorist here could teach me a lesson in the comments thread below? Thank you very much!





Comments