The late Martin Gardner held for many years a fantastic feature in the popular Scientific American magazine. It was called "Mathematical Games", and it was worth the whole magazine by itself, although SciAm always featured many interesting articles about scientific advancements. Upon picking the magazine up at a newsstand, "Mathematical Games" was the first article I would read as a teenager eager to learn about the endless tricks Gardner taught there, in his wonderful tale-telling style.
This morning my mind was still half-asleep as I got under the shower, and I started to think at one special illustration of conditional probabilities that Gardner masterfully described in one of his pieces. In truth, I do not recall the article discussing the game as a practical application of the laws of probability at all - I believe he kept wide away from exact explanations; but the article allowed you to learn by example, which is, I think, ultimately the _only_ way to really learn something.

Since I have a book project in my drawer which involves teaching probabilities to laypersons, I tried to remember how the game was exactly constructed (unfortunately, I do not have the original source available since long ago: life is a series of moves from a place to another, and every time you get rid of some stuff...). I now wish to share it with you here as I think it is quite enjoyable for its surprising twists.

The game consists in picking a spin wheel among a choice of three. On each wheel are drawn sectors with different scores on them. You and your opponent take turns to make a choice of the wheel you get to spin; then each spins his or her wheel, and the resulting scores are compared - the higher score wins the round. So below you find three spin wheels, and I am asking you to pick the one you prefer.

You will notice that the sum of the three scores on each wheel is the same - 15. Also, there can be no ties in any round, as all numbers are strictly different. I tried unsuccessfully to design the probabilities of each sector to make the dynamics work the way I wanted for a while, and then gave up and wrote a simple computer program that did it for me. I will explain later what I mean... For now, here are the three wheels:




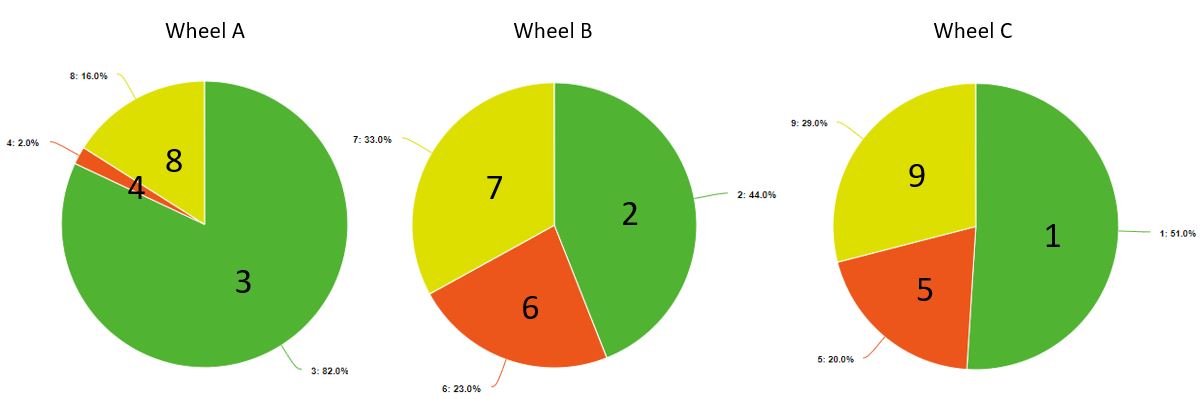
If you can't read the percentages I am listing them below: they are

For wheel A, 
p(3) = 82%
p(4) = 2%
p(8) = 16%

For wheel B,
p(2) = 44%
p(6) = 23%
p(7) = 33%

For wheel C,
p(1) = 51%
p(5) = 20%
p(9) = 29%

Now, the fun thing about this game will be explained. If you pick wheel A, you will win against your opponent in the long run, regardless of his choice of wheel B or C. In probability terms, your chance of winning a round is 52.96% against B, and of 54.20% against C. These numbers are the result of a not too complex calculation of conditional probabilities. E.g., for A vs B, you win
- if you spin a 3, and your opponent spins a 2: this happens 0.82*0.44 = 36.08% of the times
- if you spin a 4, and your opponent spins a 2: this happens 0.02*0.44 = 0.88% of the times
- if you spin an 8, regardless of what your opponent gets: this happens 16% of the times.
In total your odds against B are, as said before, 52.96%.

So, wheel A is the strongest. If you picked wheel B and your opponent unwittingly chose wheel C, however, you would still win: your total odds are of 62.2%, so B is considerably stronger than C.

But now the magic happens. A third player joins the pool, and so each one plays with one wheel against the others, and as before, the higher score wins. What wheel should you choose to have best odds? It turns out that if you stick with wheel A your odds are the lowest (30.21%)! And if you instead choose the "second-best" wheel B, your odds are better at 33.40%, but not as good as if you choose the "worst" wheel in 2-player mode, C: the odds of C in a 3-player game are 36.39%!!

This "anti-inductive" result is nothing too magic in fact - it only results from the fact that in a three-player game the importance of having high scores in your wheel become larger. 

If you are now wondering what relevance does this game have on your everyday life, I will repeat Gardner's example (IIRC). Imagine you are a habitué at a restaurant, which usually serves two possibilities for dessert in turn: sometimes they give you a choice of chocolate cake or creme caramel, some other times you can either choose chocolate cake or strawberry pie, and in other cases the choice is between creme caramel and strawberry pie. You always prefer the chocolate cake if it is available, and when you have to choose between the creme caramel and the strawberry pie you pick the former. But one evening, as the waiter explains,

"Sir, I think we have creme caramel and strawberry pie tonight - I guess you'll take the creme caramel, right?"
"Yes, that's correct, thank you!"
"Oh, but wait - they just told me there is also a choice of chocolate cake, actually! I think you prefer that, isn't that so?"
"Actually, in that case I'll take the strawberry pie!!"

It _may_ happen - the presence of a three-way choice may indeed affect your preference. But it does sound odd, doesn't it? The calculus of probabilities often offers similar situations. There is no good substitute for the direct calculation of relative odds of the different outcomes, if you have the data available. And computing conditional probabilities is not that difficult!