The plot of the week is this time a very recent result published by the ATLAS collaboration, one of the two large, multi-purpose experiments (the other is CMS, the experiment I am involved in) studying proton-proton collisions produced by the CERN Large Hadron Collider. Without further ado I paste the plot here, which I comment on below.
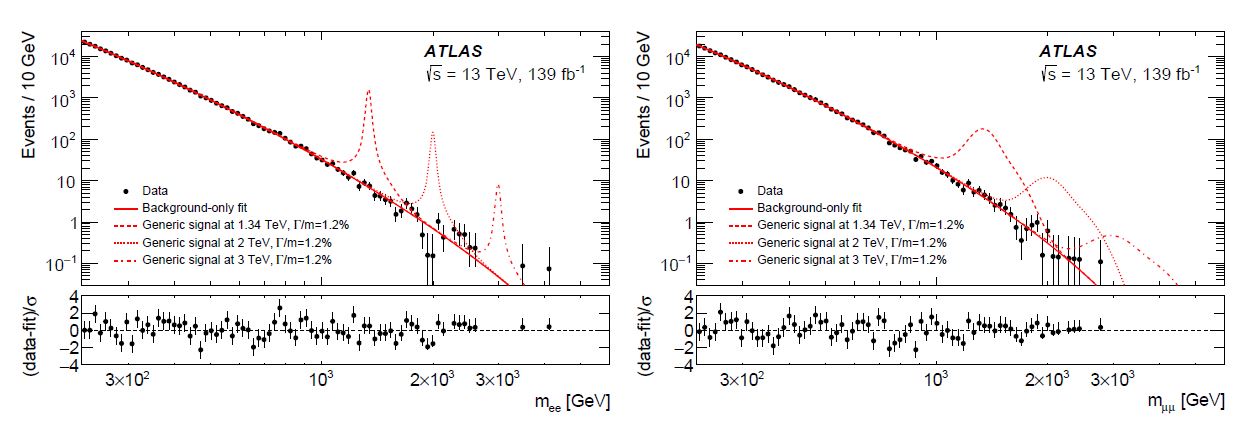
There are two panels in this graph, as the ATLAS search divided into two different but equivalent final states of the proton-proton interactions: ones producing a high-energy electron-positron pair on the left, and ones producing a high-energy muon-antimuon pair on the right. Correspondingly, you see the abscissa labeled "m_ee" and m_μμ" on the lower right of each panel.
The distributions indeed show histograms of the observed invariant mass of these particle pairs. They are semi-logarithmic, which means that the vertical axis spans several (over 5) orders of magnitudes in the frequency of population of the bins of the histogram. The highest-populated bins on the left of each graph contain over 10 thousand events each, while the bins on the right are devoid of any event.
The data are displayed, as it is customary in particle physics, as bullets with vertical bars. The bullet position identifies the number of observed events in the mass bin corresponding to the observed combined mass of the two electrons (left) or muons (right); the vertical bar reminds us that these measured event rates are random variables sampled from Poisson distributions, so there is a typical variability of the counts in each bin which corresponds to the width of the bar. But if you wanted more detail, what this way of displaying the data really means is that the experimenters are doing two things at once: reporting the observed number of events (the bullet position), which is fixed; and reporting the maximum likelihood estimate (MLE) of the event rate in the bin, which is equal to the observed counts (so it perfectly overlays with the former bullet). This MLE comes with a uncertainty which the vertical bar sizes up.
Moving on to the red curves: there are several in each panel. The full curve in each shows the model of the background - what should be observed if there are no high-mass particles contributing to the corresponding final state with decays to electron or muon pairs. And the dashed lines show instead what one would expect to observe, if there were resonances contributing to the data - with invariant masses of 1.34, 2, 3 TeV respectively.
You can note several details about the red curves. First of all, they are definitely ruled out by the observed data: the latter lines up with the background model very neatly, while they would be very different if there were resonances producing a peaking contribution. Second, electron pairs from high-mass resonance decays would produce much narrower peaks (as shown on the left) than muon pairs (on the right).
The reason for the less peaky nature of the muon distributions is that the invariant mass of muon pairs is determined by measuring the muon momenta with a different detector than that used to measure the electron energy. The former are tracking devices that record the ionization trail of the muon trajectory; the momentum is inferred by the curvature of the trajectory in the magnetic field of the ATLAS detector. The latter, used to measures electron energies, is an electromagnetic calorimeter that records the shower of electrons and photons produced by the interaction of the particles. The resulting resolution on the measured mass of the two-particle system is terrific for electrons, but not as good for muons.
A third thing to note is the up-and-down dancing of the residuals of data subtracted by background model, shown in the lower portions of each panel. These in fact show that the fluctuations are indeed what one would expect from statistical variations of the data around the background model, and shows no structure - the standard model works, and there is no need to hypothesize new heavy neutral particles decaying into energetic muons or electrons.
One small blemish in the lower panels is that ATLAS fails to report the variation of data minus fit for those bins where they observe zero events. This is a strange and - IMHO - unjustified convention, as observing zero events in a bin is exactly as informative as observing any other number, and the (negative) data minus fit result should be reported with an equal dignity as for bins with non-zero counts.
The reason of this might be (but it is hard to see if that is the case from the graph alone) that the quoted estimated root mean squares which divide the "data minus fit" numbers to produce the graphs are computed to be zero for observed zero data events in a bin (and thus embarrassing to compute for a denominator of zero): that would happen if one stuck with estimating variances of estimated Poisson mean counts by the estimated mean counts themselves. In fact, for a Poisson distribution, the mean and the variance are equal. Estimating the variance of a Poisson count with the observed counts N is very good if N is large, but for small N it causes issues of imperfect coverage of the confidence intervals.
In any case ATLAS is to be congratulated for the fast production of this neat new result, which uses a large dataset of Run 2 collisions and determines tight exclusion limits for new resonances in the several-TeV mass range. You can read more detail about the analysis in the arxiv preprint here.
---
Tommaso Dorigo is an experimental particle physicist who works for the INFN at the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the European network AMVA4NewPhysics as well as research in accelerator-based physics for INFN-Padova, and is an editor of the journal Reviews in Physics. In 2016 Dorigo published the book “Anomaly! Collider physics and the quest for new phenomena at Fermilab”. You can get a copy of the book on Amazon.






Comments