At 10¹⁴ gauss, atoms are compressed into tiny needles whose widths are only 1% of their lengths. X-ray photons readily undergo an exotic process where they change into matter and anti-matter particles briefly, before rejoining and turning back into light. Even at a distance of 1000 km, the slight polarization of water molecules would tear apart any Earth organism. So where do you find magnetic fields of such awe-inspiring strength? Attached to exotic objects in deep space, of course.

When a star has exhausted all of its nuclear fuel and it's sufficiently massive (several times the amount of mass in our own sun), it dies a spectacular death called a supernova where it ejects a large portion of its mass in a giant explosion and leaves behind a neutron star - a very dense, rapidly rotating ball of matter. Inside the neutron star, there are free electrons and protons due to the hot temperature. As these charged particles move with the rotation of the star, they generate very intense magnetic fields through a mechanism called a dynamo, which quickly drives up the magnetic field strength to approximately 10¹² gauss immediately after the star forms. The magnetic field then draws energy away from the neutron star through jets where the magnetic field lines converge at the poles, slowly reducing the rotation rate. This process forms what is know as a radio pulsar - the most commonly observed type of neutron star.


Dominating Magnetic Fields: An artist's rendition of a magnetar shows the magnetic field lines that provide most of the forces acting on the material in the star. Photo Credit: NASA

What confused researchers in the 1980's and 1990's, however, was a wave of gamma-ray radiation that swept over the Solar System in March of 1979. The wave was unusual because it repeated periodically a few times before disappearing but showed an astronomical level of energy density nonetheless. Gamma-ray bursts never come from the same point in the sky - they're typically one-time events. Additionally, the source was located 180,000 light years from Earth, in the Large Magellanic Cloud, meaning that the total amount of energy released was truly staggering, since we only observed a small portion of it. This led to a flurry of research in the 80's and 90's as to what could have possibly caused such a strange event.

The current prevailing theory was proposed in 1992 Robert C. Duncan and Christopher Thompson from the University of Texas at Austin. They found a problem in the current theory of neutron star formation - based on the properties of the dynamo, neutron stars should actually have higher magnetic fields than were currently being measured - around 10¹⁴ gauss. They attributed this to an inefficiency in the dynamo due to an inadequate rate of rotation during the star's formation. It turned out that were the rotation rate fast enough, around 200 revolutions per second, the star's dynamo would operate at a high enough efficiency to give it a magnetic field of the magnitude predicted. Forces on the crust due to a magnetic field of that strength would overwhelm any sort of gravitational force (although those are sizable compared to our normal experience), and therefore all matter in the star should be subject to shifting due to the field. As material shifts, large changes can take place that cause huge outbursts of energy. This special type of neutron star has been dubbed a magnetar, for obvious reasons. Specifically, this type of magnetar is called a Soft Gamma-ray Repeater because of the characteristic periodicity of the incoming gamma rays.

One consequence of such a high magnetic field is the presence of large magnetic waves that propagate through the star and cause it to lose energy rapidly, mostly in the form of the spin rate. Magnetars thus have a lifetime of only about 10,000 years - a blink of an eye for cosmic phenomena. As a result, we have only found five SGR-type magnetars - four in our own galaxy and one in the Large Magellanic Cloud.


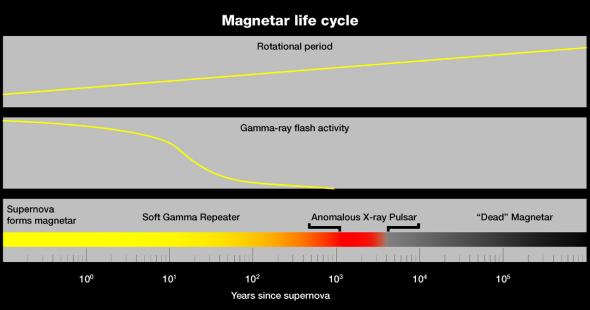
Lifelines: A diagram from NASA's website commemmorating the anniversary of the first observed magnetar burst shows how quickly they lose steam: after only about 10,000 years, they become "Dead" magnetars, which are very dim and virtually undetectable. Because the conditions required at the time of the supernova to form a magnetar are so demanding, they rarely form as well as die out quickly, leaving us mostly in the dark. Photo Credit: NASA

Recent observations haven't shed much additional light on Duncan and Thompson's theory. Very sensitive instruments on the XMM-Newton spacecraft have verified that a previously observed celestial object called SGR 1627-41 is a magnetar with a rotation rate of 2.6 seconds - the second-fastest rotating magnetar known. SGR 1627-41 flared up in 1998, emitting around 100 bursts over a six week period, but the brightness was fading quickly and astronomers weren't able to point the right instruments toward it to determine its period until now.

Sandro Mereghetti, of the INAF/Istituto di Astrofisica Spaziale e Fisica Cosmica, in Milan, and part of the team who conducted the observation of SGR 1627-41, described the difficulty in observing magnetars and how little we actually know about them: "(Magnetars) usually fade to invisibility after a few tens of thousand years. The fact that we still see this one means it is probably only a few thousand years old.... "These are intriguing objects; we have much still to learn about them."

---
'Magnetars', Soft Gamma Repeaters&Very Strong Magnetic Fields, by Robert C. Duncan at the University of Texas, Austin, contains a wealth of information.

NASA also celebrated the anniversary of the first magnetar-burst observation in 1999.