Bell curves are everywhere. Pick 100 random people and measure them: measure their height, their weight, their blood pressure, their time to run a mile, or to sprint 50 yards, and their IQ, and you find that most of us fall in the middle of the spectrum, while there are always some people on either extreme. Why?

The puzzle grows deeper when you think about genetics. If a trait like height is controlled largely by genes, how is it that height falls into a bell-curve pattern? Bell-curves seem completely at odds with what we learn about the discrete genetics of Mendel's round and wrinkled peas in high school biology.

It turns out that the solution to this puzzle is fairly simple (although the details get messy). In fact, Darwin's cousin hit on the right answer (long before he or anyone else knew about Mendel's genetics), with what he called the "Supreme Law of Unreason": a bell curve is exactly what you expect when you toss together "a large sample of chaotic elements." In other words, genetics is like one big game of The Price Is Right.

The puzzle comes from Mendel's pioneering (but ignored) genetic experiments. He found that genes act like discrete units: Snapdragons have (in a simplified example) two different versions of a color gene: one version of the color gene produces red snapdragons, while another version of that same gene produces white ones. Since each snapdragon plant gets two copies of each gene, it can have two red copies, two white copies, or one red and one white copy. These plants are either red, white, or pink, depending on which two copies of the gene they have.

Under this arrangement, only three shades of color are possible; red, pink, and white. But in nature, most traits don't fall into distinct categories. Think of human height - there is obviously no single 'height gene' that comes in small, medium and large versions. If genes can be lumped into discrete categories, how do you produce a bell curve pattern? Are there hundreds of different versions of the 'height gene'?

The first person to come up with the right answer, although he didn't know about Mendel, was Darwin's cousin, Francis Galton. Francis Galton was a pioneer when it came to applying statistics to biology, and he argued that scientists weren't paying enough attention to the message of bell curves:

It is difficult to understand why statisticians commonly limit their inquiries to Averages, and do not revel in more comprehensive views. Their souls seem as dull to the charm of variety as that of the native of one of our flat English counties, whose retrospect of Switzerland was that, if is mountains could be thrown into its lakes, two nuisances would be got rid of at once.

Bell curves, argued Galton, are telling us something about the underlying causes of biological traits - why some people are taller, stronger, heavier, or faster than others. He illustrated this idea with what is basically a modified pin-ball machine turned on its side. This device is called a Galton Board - better known today as a Plinko board, from the Price is Right:




Today's Plinko Board:



Galton in 1889:




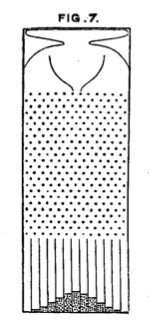
The idea is that you drop a ball in at the top, it knocks around among the pins for awhile and then lands in one of the compartments at the bottom. If you have enough compartments, and drop in enough balls, you're guaranteed to get (with an unbiased board) a bell curve  distribution of the balls among the compartments. The ball's final position depends on the sum of all of its encounters with the pins - it gets knocked to the right a little, to the left a little, and, in most cases, it ends up somewhere in one of the middle compartments. A few lucky balls get knocked to the right, over and over, and thus end up at the far right; the opposite happens for some balls that end up on the left. But by far the most likely scenario is that the knocks to the left and the right cancel each other out, and the ball ends up in the middle. There are only a few possible paths a ball can take to the extremes, and many, many ways for a ball to end up in the middle.

"This," Galton explained, "illustrates and explains the reason why mediocrity is so common."

Galton called this the supreme law of unreason:

The supreme law of Unreason: Whenever a large sample of chaotic elements are taken in hand and marshaled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along.

The more respectable and boring name used today is The Central Limit Theorem.

So what does this mean for genetics? It means that for most traits, multiple genetic factors (and, in most cases, environmental factors too) contribute to the final outcome. Imagine genes (or more accurately, genetic variants) as pins on a Plinko board: you have some genetic variants that make you a little taller, some which knock you in the smaller direction; their combined effect determines how tall you are. Only a few people are really tall, or really short, because to be really tall or short, you have to get a statistically unlikely combination of genetic variants.

This solves the puzzle posed by Mendel's experiments: individual genes may be discrete, but combinations of genes can produce traits. There is no single height gene, coming in hundreds of flavors to produce different human heights; height is instead affected by multiple genes. Bell curves are exactly what we expect to see if our height (or weight, or blood pressure, or IQ) was the combined result of multiple independent factors.

Galton puts it better:

The beautiful regularity in the statures of a population, whenever they are statistically marshaled in the order of their heights, is due to the number of variable and quasi-independent elements of which Stature is the sum.