There is a theory in economics known as the median voter theorem, attributed to Duncan Black in 1948. The theory has been used to justify the two party, winner take all system, mathematically by political economists, as the best possible system. Its conclusions are that given his assumptions, a two politician model maximizes the likelihood of a policy outcome to be closest to the policy preference of the citizens, because a politician maximize his chances of winning by choosing the mean voters policy preference. Because both parties and candidates would thus compete for the median voter, each reacts to the other's move towards the mean by moving towards the mean themselves, until they hold identical positions. However, in a two dimensional model, there are situations when it is in both party's best interest to maximize their utility simply by sticking to their own more radical rhetoric, rather than moving their
positions toward the median voter.
The assumptions of the Black's model are that voter's preferences may be measured in one dimension, and that politicians are rational in their behavior as are voters. Thus voters will choose to vote for a politician who promises to implement policies closest to their preferred policy.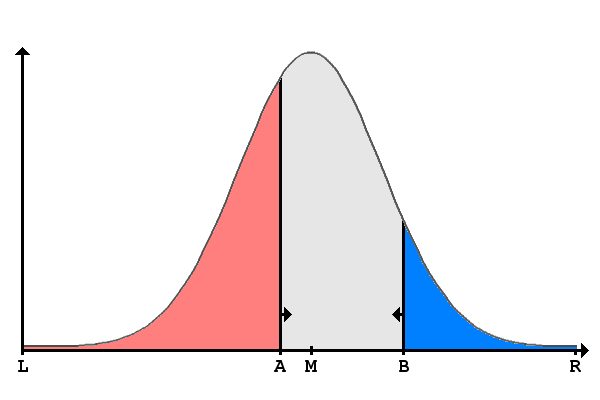
The so called nash equilibrium of this set of assumptions and players is that each politicians gravitates towards the median voter position and neither party is distinguishable. Thus, according to the theory, voters become indifferent towards the party choices.
However, in a two dimensional model, where voter preferences can fall anywhere on a two dimensional plane, a different story arises. While the median voter theorem still applies in certain geometries, there are important exceptions which create situations where the optimal political position is to maintain the extreme than support the median choice. the reason for this is that when the assumption of a one dimensional voter preference is extended into two dimensions, it is possible for a politicians to prefer los ing power to their opponent than to take the median position. this occurs when both parties are opposing in one dimension, say social progress and economic policy, but coordinated in another area, such as statist vs. libertarian. A
Assume the following variables:
di is the distance vector of the politicians from party i from the origin or median voter policy.
pi is the preferred position of the ith politican.
under a two party system i = {1, 2}
In a single dimension system, regardless of the position of the median voter, or origin of the number line, the distance between the right wing and left wing party will also be greater than the distance from the origin to their preferred positions.
Symbolically,
|p1-p2| > |p1|,| p2|. given that p1<0<p2. And according to the conclusion of Black's theorem, d1=d2 no matter what happens, since p1 and p2 must be opposing.
however, in a two dimension vector, p1 and p2 might be in opposition along one axis, but in agreement in another axis.
In two dimensions, an additional factor must come into play, which is the absolution value of the distance between p1 and p2 or |p1-p2|. When |p1-p2|<|p1|, then the preferred outcome of each political party is to keep to its own position, since the mean voter's position is farther from its own position than the position of the opposing party, despite their complete differences in one arena.
The best way to picture this is that policy decisions fall in 2 variables: x,y. And that in a two party system, for the two parties to represent approximately half of the electorate they must have at least one sign difference it its x or y variable.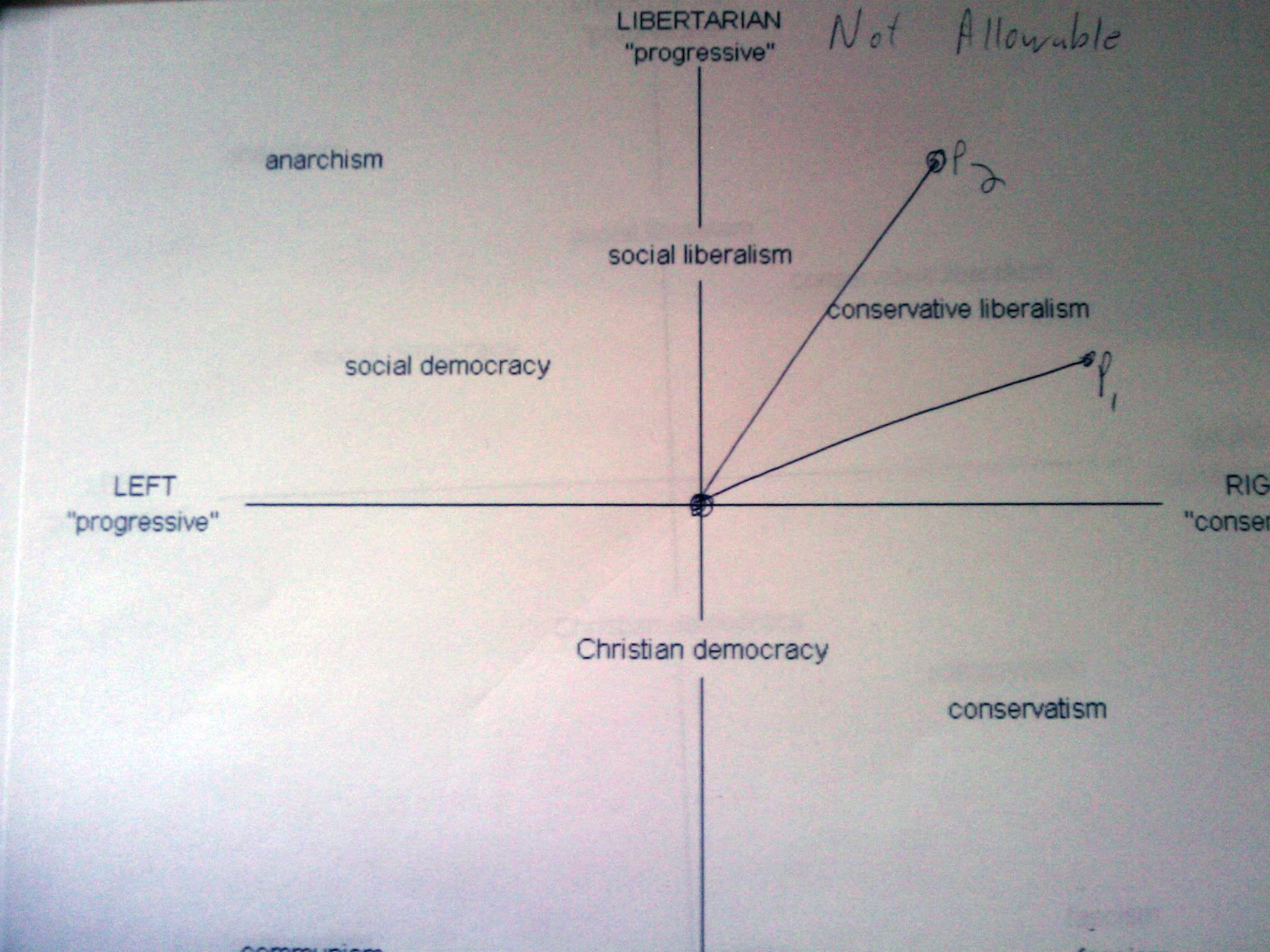
For example, x1,y1>0 and x2,y2 <0 would be allowable, as would x1,y2<0, x2,y1>0. But any case where the vectors which represent the two parties policy positions which are in the same quadrant of the two dimensional plane with the median voter at the origin, would not be allowed as representative of the electorate in any way. Further, assume that if neither party assumes a particular half of the quadrants those people will not vote.
When |d1|<|d1-p1|, the two party system follows bl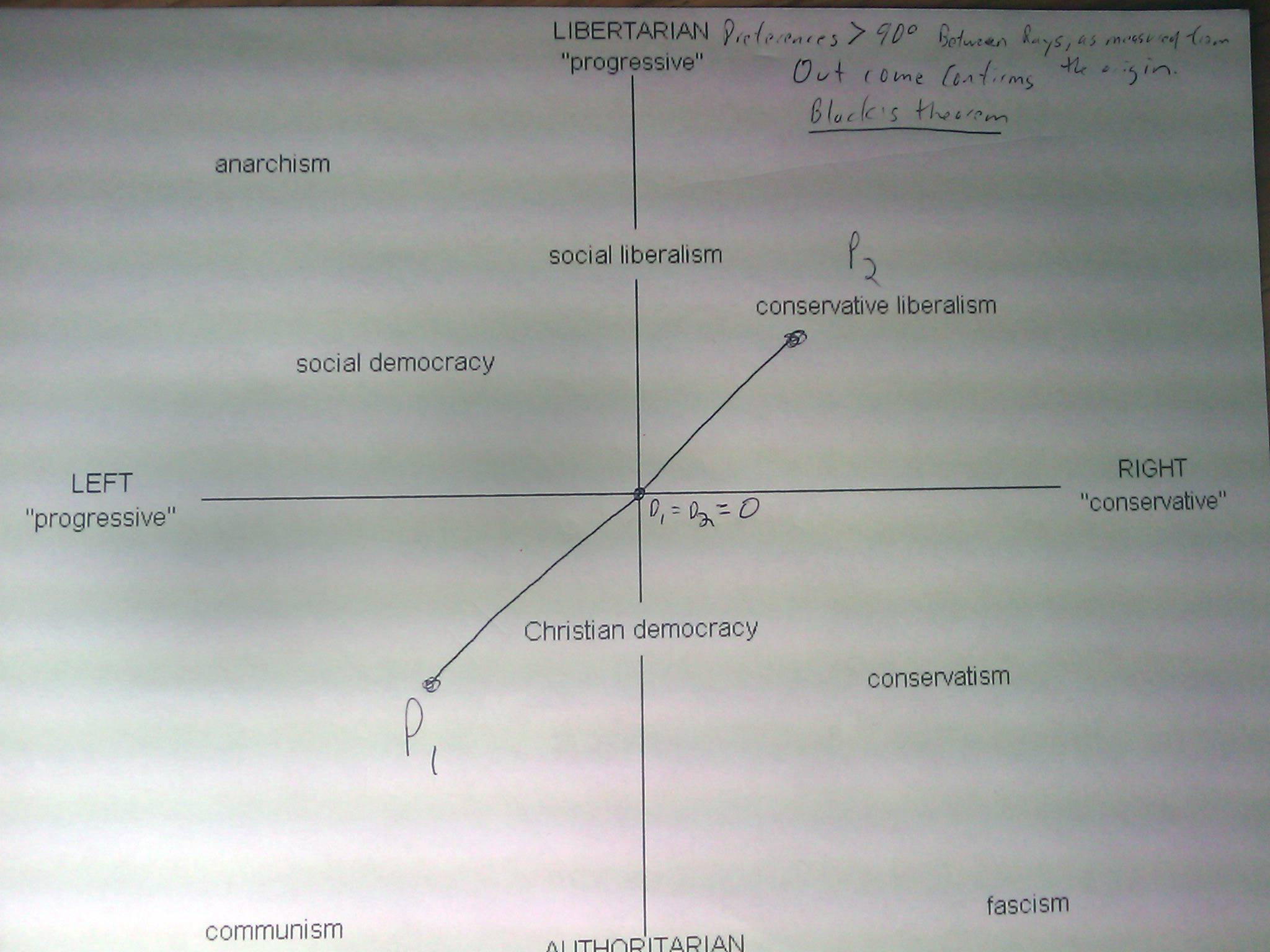
ack's model, and the rational, Nash equilibrium of the system is for both politicians to promise the medium position in their rhetoric to their voters.This is because the politician would rather see the median voter's position implemented than their opponents position implemented.
When |d1|>|d1-p1|, the rational position of a politician or political party is to take the position of the more extreme median voter of the party rather than the median voter of the general electorate.
A two dimension model generates these situations because of the possibility of triangularity in policy preferences. If we vector notational, as well as set the origin of the coordiinate plane as the median voter's policy choice, we may begin to understand this phenomenon mathematically.
One additional postulate of the two dimensional model is that the ratio of the distance di of the policy choice to the sum of all , all the policy choices, d1+d2, provides a measure of the expected outcome of an election. rather than the absolute outcome as traditional models postulate. Thus, Probability of party 1 winning is
P1={1-|d1|/(|d1+d2|)
Furthermore, the degree of preference for a policy choice may be turned into a normalized vector, by dividing the vector U1=|p1-p2|/(|p1-d1|+|p1-p2|), which gives a measure of the ratio of preference between the declared policy choice and the opposition's policy choice, or the Utility of a particular policy position in standard economic jargon.
.
The expected value to party 1 taking a particular position is thus another normalized variable, where E1=U1*P1
While, in a one dimensional linear system, both parties rational choice is to pursue the median voter,since it both maximizes his probability of winning, as well as his utility, in a two dimensional system, there is a threshold after which the expected utility of a policy position is lower than the utility of the opposition party's policies to party 1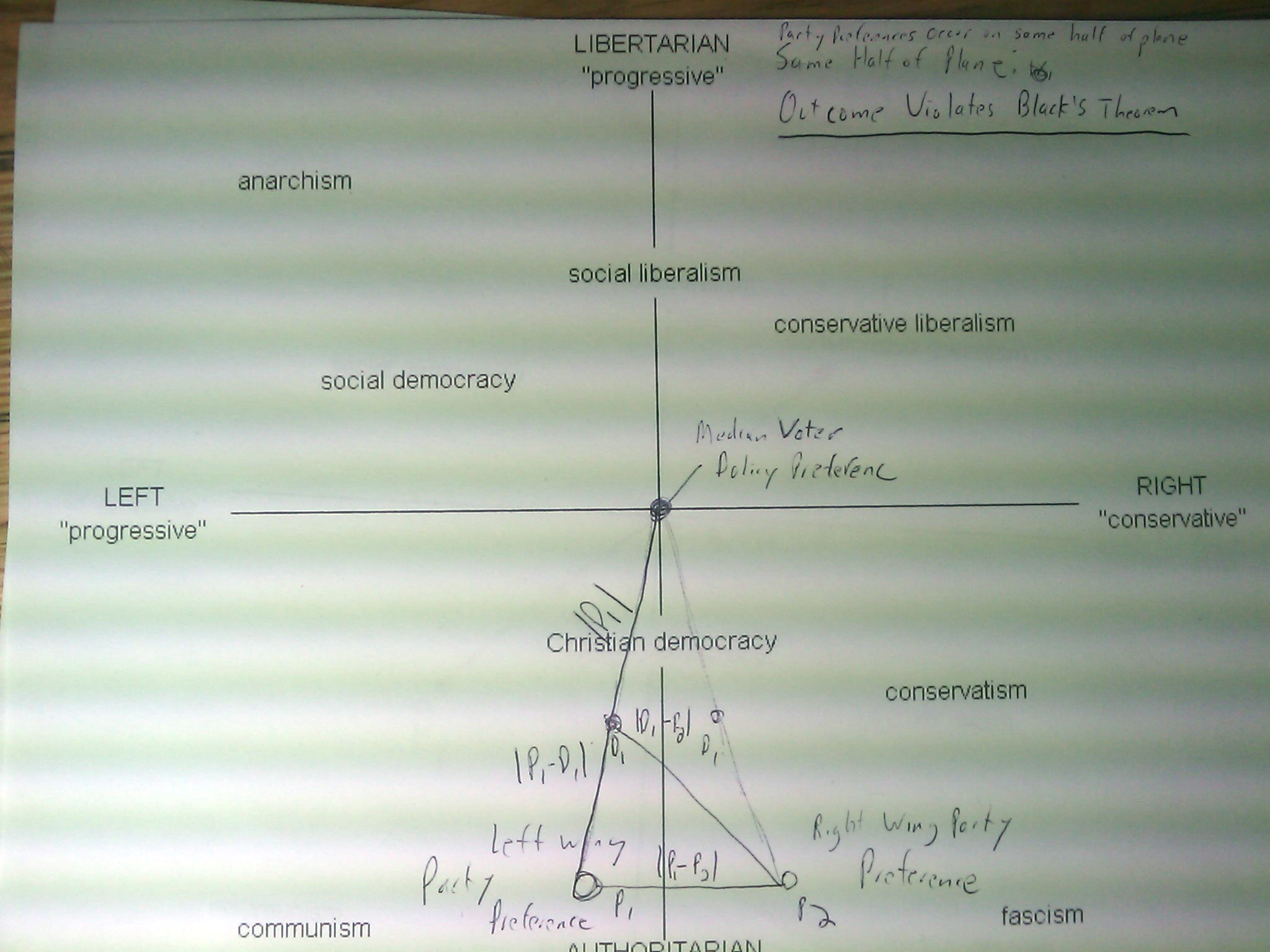
if party positions are in the same halves of the two dimensional plane. Beyond this threshold, it is in both party's best interest to maximize their utility simply by sticking to their own more radical rhetoric, rather than moving their positions toward the median voter. Since they would gain more utility if there opposing party won than if they moved towards the median voter policy preference.
One hypothetical example is when two parties expouse an authoritarian execution of their ideology. Though they have opposing ideologies, their methodology is relatively identical. Thus, where they are close to the mean voter in one dimension, they are far removed from the mean voter in two dimensions. This creates a situation where an approach to the mean voter is an irrational choice in a multi-step game with the opposition party, if the opposition parties ideologies only oppose on one dimension and their ideologies are close enough. While a movement towards further radicalism causes a net loss among established voter who fall in the same half of policy dimension on which the two parties agree, it creates the potential to temporarily mobilize voters who do not participate in the system because of alienation from the authoritarian outlook of the two parties in this hypothetical system. In the long term, a swing towards radicalism will not create a net gain for either party, but it is possible that a short term gain among disaffect voters may occur.
Other examples abound.
positions toward the median voter.
The assumptions of the Black's model are that voter's preferences may be measured in one dimension, and that politicians are rational in their behavior as are voters. Thus voters will choose to vote for a politician who promises to implement policies closest to their preferred policy.
The so called nash equilibrium of this set of assumptions and players is that each politicians gravitates towards the median voter position and neither party is distinguishable. Thus, according to the theory, voters become indifferent towards the party choices. However, in a two dimensional model, where voter preferences can fall anywhere on a two dimensional plane, a different story arises. While the median voter theorem still applies in certain geometries, there are important exceptions which create situations where the optimal political position is to maintain the extreme than support the median choice. the reason for this is that when the assumption of a one dimensional voter preference is extended into two dimensions, it is possible for a politicians to prefer los ing power to their opponent than to take the median position. this occurs when both parties are opposing in one dimension, say social progress and economic policy, but coordinated in another area, such as statist vs. libertarian. A
Assume the following variables:
di is the distance vector of the politicians from party i from the origin or median voter policy.
pi is the preferred position of the ith politican.
under a two party system i = {1, 2}
In a single dimension system, regardless of the position of the median voter, or origin of the number line, the distance between the right wing and left wing party will also be greater than the distance from the origin to their preferred positions.
Symbolically,
|p1-p2| > |p1|,| p2|. given that p1<0<p2. And according to the conclusion of Black's theorem, d1=d2 no matter what happens, since p1 and p2 must be opposing.
however, in a two dimension vector, p1 and p2 might be in opposition along one axis, but in agreement in another axis.
In two dimensions, an additional factor must come into play, which is the absolution value of the distance between p1 and p2 or |p1-p2|. When |p1-p2|<|p1|, then the preferred outcome of each political party is to keep to its own position, since the mean voter's position is farther from its own position than the position of the opposing party, despite their complete differences in one arena.
The best way to picture this is that policy decisions fall in 2 variables: x,y. And that in a two party system, for the two parties to represent approximately half of the electorate they must have at least one sign difference it its x or y variable.
For example, x1,y1>0 and x2,y2 <0 would be allowable, as would x1,y2<0, x2,y1>0. But any case where the vectors which represent the two parties policy positions which are in the same quadrant of the two dimensional plane with the median voter at the origin, would not be allowed as representative of the electorate in any way. Further, assume that if neither party assumes a particular half of the quadrants those people will not vote.When |d1|<|d1-p1|, the two party system follows bl
ack's model, and the rational, Nash equilibrium of the system is for both politicians to promise the medium position in their rhetoric to their voters.This is because the politician would rather see the median voter's position implemented than their opponents position implemented.When |d1|>|d1-p1|, the rational position of a politician or political party is to take the position of the more extreme median voter of the party rather than the median voter of the general electorate.
A two dimension model generates these situations because of the possibility of triangularity in policy preferences. If we vector notational, as well as set the origin of the coordiinate plane as the median voter's policy choice, we may begin to understand this phenomenon mathematically.
One additional postulate of the two dimensional model is that the ratio of the distance di of the policy choice to the sum of all , all the policy choices, d1+d2, provides a measure of the expected outcome of an election. rather than the absolute outcome as traditional models postulate. Thus, Probability of party 1 winning is
P1={1-|d1|/(|d1+d2|)
Furthermore, the degree of preference for a policy choice may be turned into a normalized vector, by dividing the vector U1=|p1-p2|/(|p1-d1|+|p1-p2|), which gives a measure of the ratio of preference between the declared policy choice and the opposition's policy choice, or the Utility of a particular policy position in standard economic jargon.
.
The expected value to party 1 taking a particular position is thus another normalized variable, where E1=U1*P1
While, in a one dimensional linear system, both parties rational choice is to pursue the median voter,since it both maximizes his probability of winning, as well as his utility, in a two dimensional system, there is a threshold after which the expected utility of a policy position is lower than the utility of the opposition party's policies to party 1
if party positions are in the same halves of the two dimensional plane. Beyond this threshold, it is in both party's best interest to maximize their utility simply by sticking to their own more radical rhetoric, rather than moving their positions toward the median voter. Since they would gain more utility if there opposing party won than if they moved towards the median voter policy preference.One hypothetical example is when two parties expouse an authoritarian execution of their ideology. Though they have opposing ideologies, their methodology is relatively identical. Thus, where they are close to the mean voter in one dimension, they are far removed from the mean voter in two dimensions. This creates a situation where an approach to the mean voter is an irrational choice in a multi-step game with the opposition party, if the opposition parties ideologies only oppose on one dimension and their ideologies are close enough. While a movement towards further radicalism causes a net loss among established voter who fall in the same half of policy dimension on which the two parties agree, it creates the potential to temporarily mobilize voters who do not participate in the system because of alienation from the authoritarian outlook of the two parties in this hypothetical system. In the long term, a swing towards radicalism will not create a net gain for either party, but it is possible that a short term gain among disaffect voters may occur.
Other examples abound.
Comments