Fractals: Form, Chance and Dimension was published in English in 1977 (the original French came out two years earlier) but the book that sealed Mandelbrot's fame as an original thinker was the 1982 classic, The Fractal Geometry of Nature. It is one of those rare books that can be read both by professionals and lay readers. It also helps that it is copiously illustrated so that even if the mathematics may appear esoteric just relax and enjoy the visual candy.
You can read about the life of Benoit Mandelbrot in a variety of places and there must be millions of fractal images around the net. On a personal note this news item reminded me of my school days. In 1980 I was studying mathematics A levels which included iterative solutions to the roots of polynomials. It was obvious that sometimes this worked... and sometimes it didn't. Sometimes the algorithm converged to the nearest root and sometimes it diverged. The textbook explained this in terms of the geometry around the root but it raised an obvious question: was there a point where the solution neither converged nor diverged? I played around with the coefficients a bit and indeed found that there were unstable iterations.
The Father of Fractals: the Mandelbrot Set.
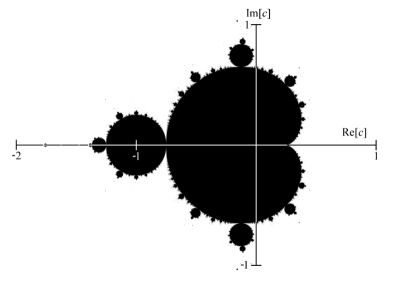
Indeed, the whole thing was ludicrously simple when reduced to the difference equation. I'd never heard of Mandelbrot at the time, and these were the days before personal computers and I didn't have the luxury of Gaston Julia manually calculating each iteration while convalescing in bed; the next topic in the course was beckoning and my little discovery lay forgotten. Anecdotal proof that it's not just a matter of finding something new but realising its importance. Something that Mandelbrot achieved in bringing together fragments of previous research that had laid unconnected.
Back to Mandelbrot, here's a link to his last talk at a TED conference entitled Fractals and the art of roughness.



Comments