Quantum entanglement is a well observed but not well understood phenomena.  The frontier in this area has been to entangle systems at greater and greater distances.  Theoretically however it is poorly understood.  Susskind and Maldacena proposed the ER=EPR conjecture, which to oversimplify, states that entangled particles are connected by tiny wormholes(Maldacena and Susskind)  In this brief blog post I present a simple proof that the “non-locality” that experimentalist write of, and Susskind conjectured about solving via wormholes, can be explained with standard quantum mechanics and standard relativity.   What is new here is how we look at the spaces involved.

The precise nature of the spaces involved is the key to understanding the phenomena of entanglement.   In short Alice and Bob start out with separate states that they entangle. Creating one state in a common Hilbert space which is the tensor product of the original states.   When Bob travels to his lab he takes his state with him.  Mathematically and physically this can be thought of as a series of general transformations and Lorentz transformations as he accelerates, and travels at a steady velocity, then comes to rest in his labs frame of reference. 

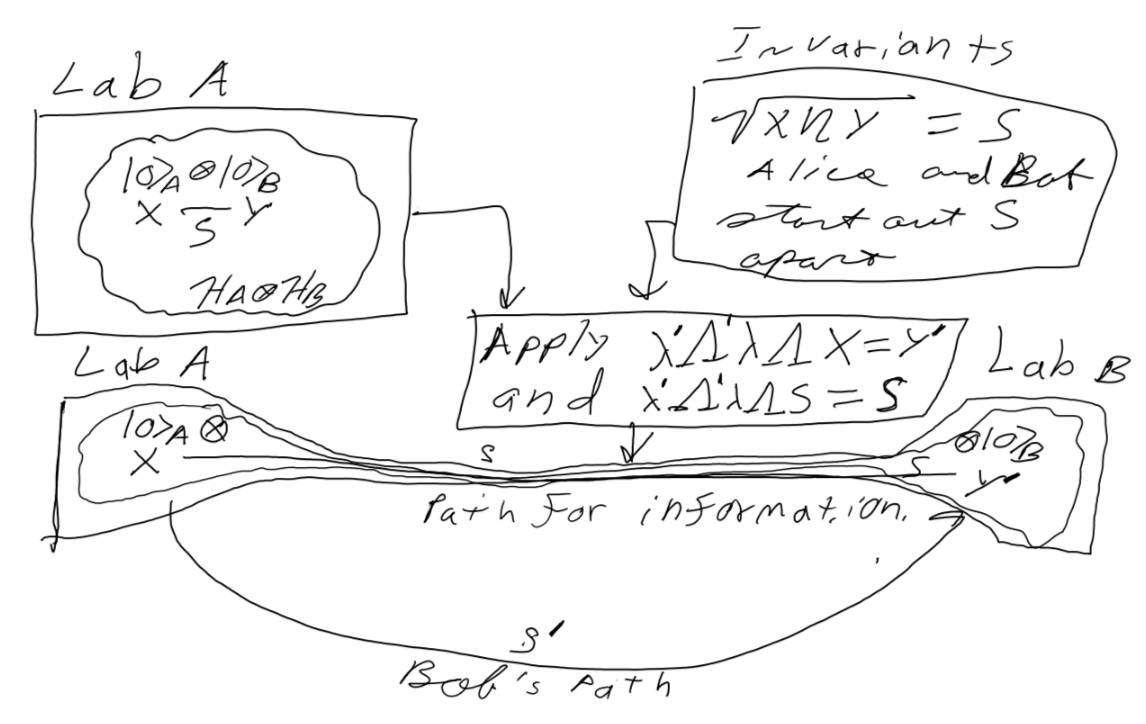
Here is where the misconception comes in.  To an experimentalist eye Alice and Bob now occupy distinctly separate spaces several light seconds or light minutes apart. The correlation between Alice’s observations of her state and Bobs observations of his state appear to violate special relativity.  However, if we sit and think about the math and do the math that’s not the case at all.  Even without invoking wormhole solutions to Einstein’s equations this can be shown.     Consider the figure.

Alice and Bob prepare quantum states that they entangle.  Alice’s state is at spacetime point X and bobs is at space time Point Y and they are separated by an invariant interval S.  After a series of transformations Bob arrives at his lab via path S’ and observes “non-locality” because of the misconception that quantum information would only have the single classical path available for him and Alice to observe.  Like, neighborhoods on opposite sides of a city connected by a 16 lane expressway  can be more “local” than ones a mile or two apart with congested one way streets between them.

Bob takes his part of the entangled state and travels to his office.  Mathematically and physically this can be thought of as a series of transformations which increase the observed invariant interval from S between Alice’s state located at X and Bob’s state now located at Y’ an apparent interval S’ away.

My full handwritten notes that lead me to this are at this link. 

The key misunderstanding comes from thinking that S’ the apparent invariant interval between X and Y’, the path Bob himself took as he transported his state is the same path that information must necessarily take from X to Y’.  

Quantum information also has available to it the shortcut S.  S is an invariant interval as such it would not change under transformation.  The X Y Z and t components may change but S itself is by construction and definition invariant.    So, to the quantum particles and to quantum information S is just as available as S’. 

In fact, since S is a shorter path more information would likely pass by S than by S’.    Yet it does not violate special relativity at all and does not need a wormhole to accomplish this feat.   The answer lies in combining Quantum Mechanics with Special Relativity.  Putting this in full algebraic quantum field theory terms would make it neater but not that much more clear.  To see what that looks like my earlier papers on relativization address that (Farmer).

So why don’t Alice and Bob observe the same shorter interval S as their quantum states do?   

Why don't we see these "wormholes" or shorter intervals ourselves? 

That question is answered in detail by the second reference below (Sperling and Walmsley).  For this blog, I will shorten it and anyone who wants more detail really should read  (Sperling and Walmsley).  The entanglement we’d see would be a statistical phenomenon manifesting in the quantum states of their constituent particles.  Furthermore, in a macroscopic system like a person the constituent particles are constantly interacting with each other forming new stronger entanglements.   

Without veering into metaphysics and paranormal ideas where people who are friends, family, or lovers have a “sixth sense” about the state of a physically distant person, statistics about large ensembles of particles are all we can discuss. 

References

 BIBLIOGRAPHY Farmer, Hontas. n.d. "Fundamentals of Relativization." The Winnower. doi: 10.15200/winn.141487.76774.

Maldacena, J., and L. Susskind. n.d. "Cool horizons for entangled black holes." Fortschritte der Physik. doi:10.1002/prop.201300020♠.

Sperling, J., and I. A. Walmsley. n.d. "Entanglement in macroscopic systems." Physical Review A. doi: 10.1103/PhysRevA.95.062116.