In other words, if such particles exist they must be more massive than a thousand protons. The limit is M(Z')>1071 GeV, so to be precise Z' must be more massive than eleven hundred and forty protons, since a proton weighs 0.938 GeV. Or if you need an alternative unit of measure, let's take my own body weight after christmas parties are over: at 72.5 kilograms I weight about 43.3 thousand trillion trillion protons, so we can also say that Z' bosons must be heavier than 26.3 thousandths of a trillionth of a trillionth of a Tommaso. If I carried a handful such particles in my pocket, you would not notice the difference.
Three minutes of boring theory before the exciting new result
As I have grown accustomed to do when time allows, before offering the interesting new experimental result I get a bit didactical. Given that this medium does not guarantee much concentration from the reader, I will constrain this introduction to three minutes worth of text. Of course, if you are knowledgeable or impatient, you are free to jump to the next section...
Z' (read: Z-prime) bosons are ubiquitous in extensions of the gauge group SU(2)xU(1) on which the Standard Model is based, whenever a U(1) group is added to the structure. U(1) is the one-dimensional unitary group, and it can be represented by rotations on a plane. Rotations are parametrized by an arbitrary angle, or phase -let us call it
. To understand what is the connection between this rotations group and the physics of elementary particles, we may suppose that to each point of space can be associated a small dial with one hand. The angle (with respect to a fixed direction) the hand aims at is immaterial, and does not modify the properties of space: in quantum-mechanical terms, an arbitrary choice of the angle in a point of space corresponds to multiplying the wave-function of our physical system in that point by a unobservable complex phase. Please do not be scared by the term "wave function": it is just a mathematical expression which may be describing, for instance, a single electron in quantum mechanical calculations.
The important thing is that we cannot observe wave function amplitudes (complex numbers) but only the resulting intensities (real numbers!), which are obtained by taking the squared modulus of the amplitudes. Because of that, the phase is irrelevant for the observable physics: the squared modulus of the phase is equal to unity, so
never appears in the expression of observable, measurable quantities! In other words we should be free to orient the hand of each dial anywhere we like without our experiments being sensitive to the choice.In the course of the past century physicists have understood that their theories, in order to represent the reality of the mechanics of particles, need to be "gauge invariant". Gauge invariance is the requisite that the behaviour of elementary particles (i.e., their predicted future history given a set of initial conditions) is to be left unmodified by an arbitrary choice of the phases in every point of space.
The classic example is electromagnetism: one starts with a description of electrons as wave functions of point charges with spin in an electromagnetic field. Once one allows that an arbitrary phase, different in every space-time point, multiplies the wave function of electrons, and one insists that this does not affect their dynamics, one is mathematically forced to admit that a new vector boson exists: this particle is the "messenger" of the interaction, which connects the different space-time points sewing them together and canceling the different complex phases. This vector boson is the photon, the quantum of the electromagnetic field.
The arbitrariness of the phase corresponds to a "invariance" of the physical laws under the choice of this parameter. It has been known for about a century that to such an invariance must correspond a conservation law. The conservation law in question, for electromagnetism, is that of electric charge: the theory constructed with local gauge invariance guarantees that the number of positive minus negative electric charges is a constant.
Now, it is very tempting to hypothesize that the gauge group of elementary particles contains an additional U(1) group besides the one that generates the photon. Such an extension would have several attractive properties, and indeed theorists have generated a set of theories all based on additional U(1) groups. Add a U(1) group to the theory, and you gain the privilege of posing the existence of a fifth force, a new kind of electric-like charge, and a number of as-yet unseen phenomena. Isn't that cool ?
In prosaic terms, all of the proposed extensions imply the existence of (at least) a new gauge boson. Such a boson must be electrically neutral, and massive -otherwise we would know it already! In fact, it must be so massive as to have eluded previous searches. At a collider, the more massive a particle is, the less frequently it is produced. This is the way theorists keep their theories alive: by posing that the particles their theories predict have been hiding where they could not be spotted until yesterday. But experimentalists with their searches gradually restrict the domain of existence of these theories, by excluding parts of the allowed parameter space. That is what CDF is doing with the unknown Z' mass.
The CDF search
Okay, theoretical introduction over. Now that you understand that these beasts must hide, if they exist, at large masses and low production rates, and that they are neutral and massive, you also may guess how we look for them. A Z' boson produced in a proton-antiproton collision will, a fraction of the times, decay into a pair of charged leptons: electron-positron, or muon-antimuon pairs. Tau pairs, of course, are less attractive due to the difficulty in separating these from hadronic jets; quark-antiquark pairs are even harder; and neutrino pairs are simply a nightmare, since neutrinos will escape unseen (we can still detect their departure, just as if, blindfolded and deaf and rowing in a boat, we suddenly feel the boat tilting on our side: our friend on the other side must have fallen in the water!). Muons and electrons of high energy are equally powerful signatures, but the new CDF analysis utilizes the former.
The search for high-mass dimuon pairs is based on a data sample corresponding to an integrated luminosity of 4.6 inverse femtobarns of proton-antiproton collisions. What this means is that the set of events are collected from a total of just a bit less than 400 trillion collisions. This number is easy to compute: the total proton-antiproton cross section is 80 millibarns, or 80 trillion femtobarns (since milli- stands for 10^-3, micro- for 10^-6, nano- for 10^-9, pico- for 10^-12, and femto- for 10^-15). Multiply the cross section by the luminosity and you get the number of collisions: N = 80 trillion femtobarns times 4.6 inverse femtobarns is, indeed, 370 trillions of them.
The large statistics allows CDF to look for Z' bosons which would be produced at very small rates -even a few times in a trillion, to be sure. But in order to avoid being deceived, one needs to correctly assess the background rate of processes that produce two identified muons of high invariant mass, without being due to the decay of the new Z' boson. This is indeed the hardest part of the work: high-mass dimuon pairs can be produced by the Drell-Yan process (that is, decays of Z bosons, or virtual photons), but also by the decay of top quark pairs, or of pairs of W bosons; they also may be the result of hadrons that fake the muon signature; and finally, one must beware of cosmic rays -muons produced in the upper atmosphere, which may cross the detector at its center and get reconstructed as two separate muons of opposite charge!
All the possible background processes are computed with a number of different methods, and their sum is evaluated as a function of the invariant mass they would produce. The total expected spectrum is shown in the figure below; the black points with error bars show the observed data.
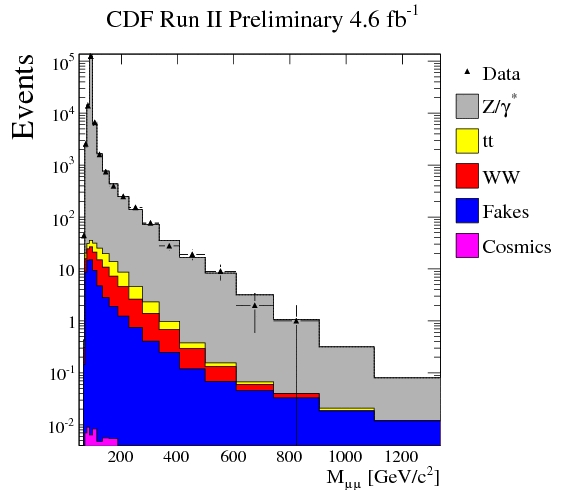
It is clear by simple visual inspection that the data agree with the expected backgrounds. The comparison, performed with the help of some complicated statistical method, allows to extract a so-called "upper limit" on the production cross section of Z' bosons, as a function of the mass of the particle. This upper limit is the maximum production rate of the particle given that it has escaped detection in the analyzed dataset. The upper limit is shown by the red curve in the figure below.
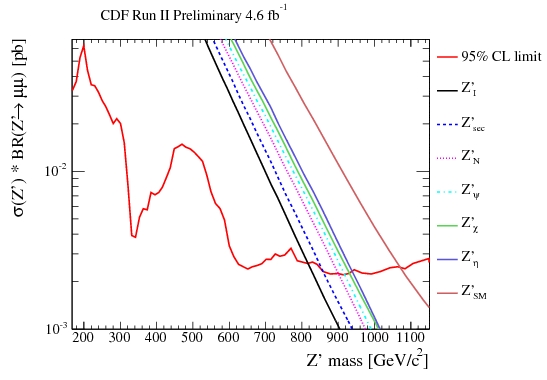
In the figure are also shown the expected rates predicted for different kinds of Z' bosons, in different theoretical models. By comparing the upper limit with the theoretical curves, one may deduce that the Z', if it exists, must be heavier than the mass value corresponding to where the theoretical curves intercept the red curve. That is because for lower masses the predicted rate would exceed the observed upper limit.
The described exercise allows CDF to exclude that Z' bosons, if they exist, have masses below 1071 GeV. This value corresponds to the "simplest" kind of Z' bosons; the different models predict enhanced or suppressed rates of production and/or decay into muon pairs, such that the corresponding limits are higher or lower than the quoted one.
In summary...
To summarize, CDF excludes the existence of new Z' bosons of mass below a TeV or so. This limit is probably the last one that CDF will produce in its long and illustrious career: the LHC experiments ATLAS and CMS, with their bounty of 7-TeV proton-proton collisions, are already in the position of extending the search to much higher mass values, effectively putting CDF and DZERO out of business in this particular research topic. Such new improved limits are probably going to be produced soon... Unless a Z' boson does finally appear at the LHC!
For more information on the CDF analysis, please see here.
Comments