First of all, let me tell you that quirks so far have only been found in the dream of a few theorists. There is no necessity for their existence, although they could indeed be part of our world and have happily lived undetected this far. Searching for the Unknown is one of the most entertaining activities of particle physicists, and there needs not always be a strong theoretical motivation: quirks just might exist, so let us hunt them -we might step in a Nobel prize!
The theoretical idea is that Nature might feature a replica of the SU(3) group which governs the strong interaction of quarks; this would bring in a new force, which we might call "infracolor". The new force would be felt only by quirks, which would thus live undisturbed in their "hidden valley". As for us, being made of quarks we would not feel any infracolor.
Foncused by my mention of group theory ? Fear not, we are only going to talk about very down-to-earth phenomena for the rest of this article. In fact, the signature of the production of quirks and the infracolor force at a proton-antiproton collider is a very striking one, which has nothing exotic per se: the appearance of a good-old ionization track, but one which is perfectly straight and which is made up by abnormally large ionization energy deposits along its trajectory.
Quirks are supposedly endowed with electrical charge, and a quirk-antiquirk pair produced in a proton-antiproton collision would create a neutral, loosely bound state, where the two constituents are separated by a macroscopic distance, amounting to several tens of micrometers. So the neutral "particle" they compose would have a sufficient spatial extension that its internal "electric charge distribution" (localized on the two quirks) would actually ionize the medium through which it travels, something that regular neutral, pointlike bodies cannot do. And the ionization would be large, because we are talking of a massive body which is moving slowly for subatomic particle standards.
Ionization is one of the means by which a subatomic particle endowed of electric charge loses energy in traversing a medium. What happens is simply that the moving charge interacts with the electromagnetic field of the atoms by exchanging photons with them, kicking the sources of the field -the atomic electrons- off their orbits. In doing so the particle yields energy to the medium and it slows down, at a rate which is quite well-known and which depends on the particle speed. Slow-moving charges ionize the medium much more strongly, as one can verify by studying the figure below.
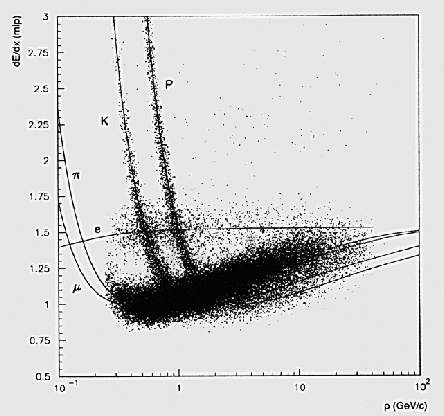The figure on the right shows the correlation between particle momentum - the quantity plotted on the x axis- and energy release per centimeter of traversed material -on the vertical axis. Each point is a detected charged particle for which these two measurements were made. Ignore the high density of points along the pion line on the bottom -the relative population of the different curves has no meaning. Instead, you immediately observe several highly interesting features in the plot. If you follow from left to right (increasing speed) the curve for pions, kaons, or protons (labeled with the greek pi symbol, K, and p, respectively), you realize that particles sustain large specific energy losses if they are traveling slowly, then their loss hits a minimum in a wide range of speeds, and then the loss increases again if the speed is very high (ultra-relativistic). These features are all well-understood results of quantum electrodynamics, and we need not be concerned with their origin; what matters is that two particles of different mass and same momentum behave quite differently: in fact, in rough terms we can say that what matters is speed, not momentum. Remember: in non-relativistic regimes, momentum is the product of mass and speed. Different mass and same speed give different momentum, so the various particle species cluster in separate curves.
So here we are looking at a very nice way to distinguish different particles! We can measure momentum from the curvature of tracks in a magnetic field, and if we measure energy loss too, we gain access to the particle identity. That is what the graph implicitly shows by the labels of the different clusters of points: muons, protons, electrons, pions have different masses, so for the same momentum they yield different energy loss.
And what would a quirk-antiquirk loosely bound state look like in such a graph ? Its curve would be a translation toward the right of the other curves: being much more massive than all particles shown in the graph, the ionization for such a bound state would be quite large for a wide range of momenta. Things are not exactly trivial, but the specific ionization loss can indeed be calculated using the kinematics of the bound state and the relative motion of the two quirks "within" it.
Armed with that knowledge, and with a beautiful silicon detector (see the above figure) capable of recording the ionization charge left by tracks in the silicon layers, DZERO sought straight tracks with a large associated ionization in their data. In order to be triggered, the event featuring a quirk-antiquirk pair creation must contain at least one recoiling hadronic jet, caused by regular QCD radiation. Real signal events would also feature a large transverse momentum imbalance, because the quirk-antiquirk system showing no curvature in the magnetic field would look like a track of very high momentum. The missing momentum would be aligned with the straight track.
(Let me open a parenthesis for the benefit of those of you not familiar with transverse momentum imbalance. When a proton and an antiproton collide in the core of DZERO, they produce particles all over the place, that leave the interaction point with large momenta in any directions. However, the sum of their momenta computed in the plane transverse to the beam direction must be zero, because of a simple rule of dynamics. What the detector records in general is a non-null combined momentum for the final state particles, because of imperfections in the measurements and because of neutrinos escaping unseen. A neutral particle leaving a straight track would cause a failure of the missing momentum measurement, because it would be interpreted as a very high-momentum particle when in fact its momentum can have any value!)
The signature of a quirk-antiquirk pair recoiling against a jet may be mimicked by W boson production events: a W boson decaying to a lepton-neutrino pair if produced in association with a energetic jet may feature a energetic track and large missing energy due to the escaping neutrino. Also simple QCD multijet production may produce backgrounds. These processes are reduced with several kinematical cuts, which we need not discuss in detail here. The result is that DZERO selects 4632 events and proceeds to examine the specific energy loss (labeled dE/dx) of the candidate quirk-antiquirk track. The distribution is shown below.
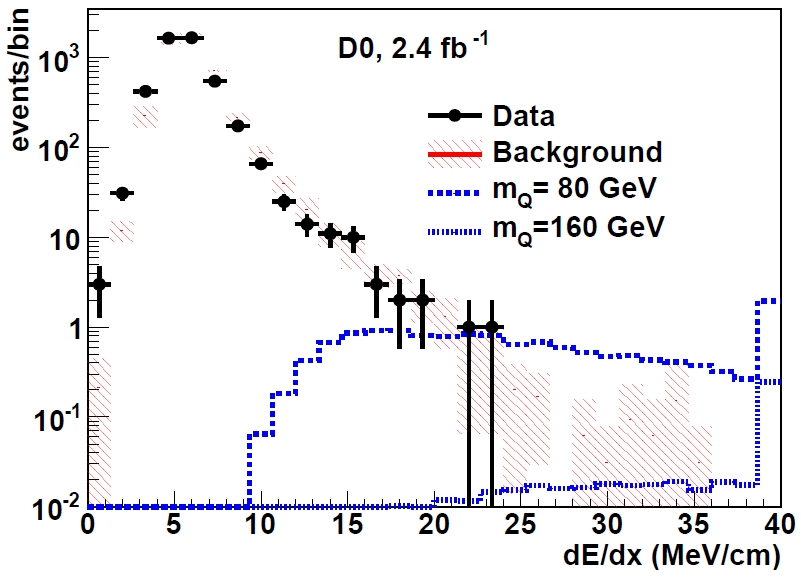
As you can see, the data (black points) closely match the expected background distribution (red hatched histogram), calculated with the various background contributions and the known specific energy losses of the relevant stiff tracks in those events. The blue curves instead show what kind of a distribution would be expected for quirk-antiquirk pairs of different masses. It is quite evident that no such signal is hiding in DZERO data.
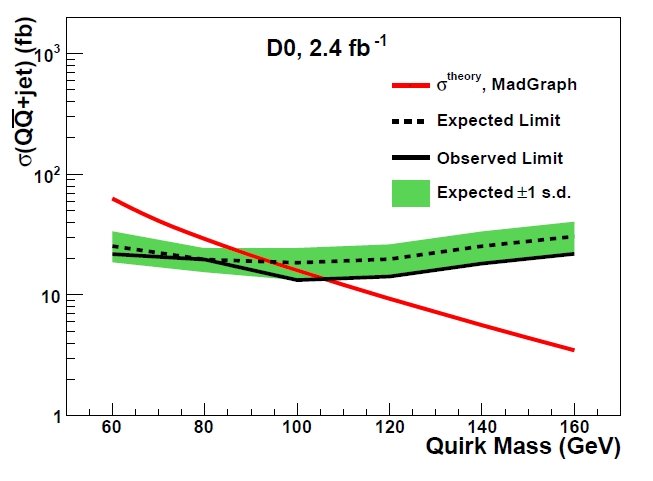Based on the dearth of high-ionization tracks in the selected sample, DZERO is able to set a limit on the production cross section of the exotic process. The limit, shown by a black curve in the figure on the left, depends on the hypothesized quark mass, because the particle mass would affect the detection efficiency. By comparing the observed limit with the expected production rate (in red), one can decide that quirks, if they exist, must be more masive than 110 GeV, because if they were lighter they would have shown up in the tail of the dE/dx distribution.So quirks are not there, or they are very massive. Their existence cannot be plainly disproved: alas, that is one frequent problem of collider physics searches: you can only push the boundary further, but you can never put the final word on the hypothesized existence of massive new particles. On the other hand, maybe one of these off-the-beaten-path searches might one day turn out to become the discovery of the decade!
Comments