The conversion of a real, energetic photon into a fermion-antifermion pair readily occurs when the particle traverses a medium: the process is also known as "pair production", and is the leading form of energy loss of energetic photons in matter. It is thanks to it (and to the related process called "bremsstrahlung" of energetic electrons) that our electromagnetic calorimeters can measure electrons and photons!
The process is increasingly likely if the medium contains high-Z atoms, which are more readily capable to absorb the extra momentum that the photon must lose in order to convert. In fact, in vacuum a real photon simply cannot convert, since the process would violate the conservation of four-momentum. And in fact, calorimeters are built with high-Z materials (ever wondered, for instance, why CMS has an incredibly expensive lead-tungstate crystal electromagnetic calorimeter ? The high Z number of lead is the answer).
So, we are talking of an extremely well-known physical process here. We know that photons convert into light particles, so muon pairs are very rarely the result; photon conversions essentially only produce electron-positron pairs. But it is not only real photons that undergo the pair creation process. In fact, even "virtual" ones do. These are photons appearing as "internal legs" in Feynman diagrams: they are emitted by the initial state, and connect to the final state particles which we can observe. It is that simultaneous "double connection", the emission and immediate materialization of their energy, which allows the conservation of four-momentum.
But there is more. While the conversion of real photons is suppressed by the square of the mass of the final state fermion pair, the conversion of an internal photon is free from that constraint. Strictly speaking, the only requirement is that the energy of the virtual photon be larger than the total mass of the materialized pair. To that, you should add a factor accounting for phase space (lighter materialized particles have more possible energy configurations than heavier ones, for a given photon energy); but most of the inverse mass dependence of the reaction is absent. So internal photons may materialize into electron-positron pairs and almost as frequently into muon-antimuon pairs. Nice to know, but what is the relevance of this ?
The thing is important because multi-lepton events (where multi- means three or more) are intrinsically interesting final states at a hadron collider such as LHC. We search for Higgs bosons in these final states, as well as SUSY decays and many more other processes. And multi-leptons can arise readily from the production of a Z boson decaying to electron or positron pairs, whereby a virtual photon converts in an additional lepton pair.
It so happens that it is rare for a virtual photon to have a sufficient energy to produce a pair of leptons both energetic enough to pass our selection cuts: the latter are aimed at identifying leptons originated from the decay of heavy objects, not photons! However, what a virtual photon may do with a significant rate even if it is not very energetic is to produce an asymmetric pair of leptons: one of them very "soft", the other energetic enough to pass our cuts. These "asymmetric internal conversions" are not generally simulated well by Monte Carlo generators, providing puzzling results in multi-lepton datasets if one just runs a streamlined data-MC comparison.
Now, however, we have measured them. CMS just published a signature-based search for multi-lepton events, and among the figures contained in the paper is the one you see below.
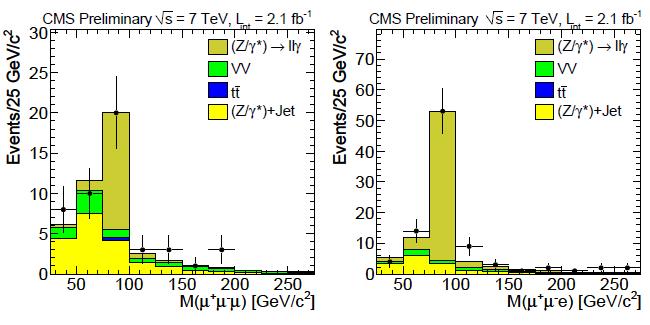
Here you see the total invariant mass of three leptons, all of respectable momenta. How is it possible to see it peaking at the Z mass value ? The reason is that these (the events represented by the dark-yellow histogram) are Z bosons which radiated a virtual photon, and the virtual photon converted into an asymmetric lepton pair. We got three leptons, not four, because the other lepton from the conversion was too soft to be detected. But it being soft, it did not contribute much to the total mass of the system: so the three-lepton mass does peak at the Z, since all these leptons collectively originate from the Z decay.
The interesting thing to see from a comparison of the two figures is that the "extra" lepton from the conversion is almost just as frequently a muon (left) as it is an electron (right)! Internal conversions are indeed not constrained by the inverse-squared-mass rule for pair production.
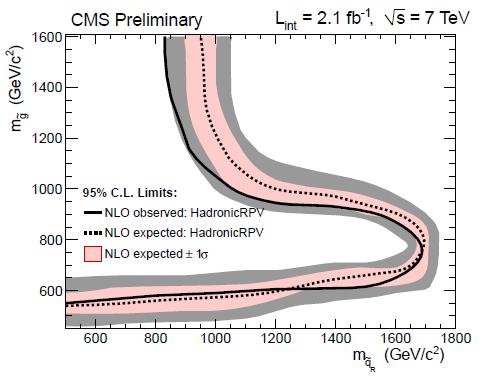 If you care to know what CMS did with the three-lepton search I mentioned, and are too lazy to follow the link to the public document, here is a sample result: the good match between data and total predicted SM processes (including internal conversions!) is used to extract limits on SUSY models with R-parity violations, which can give rise to these signatures even in the absence of large missing transverse energy. You can see one such limit on the right: the black curve divides the parameter space into an excluded (left) and allowed (right) region, depending on the value of the squark and gluino masses.
If you care to know what CMS did with the three-lepton search I mentioned, and are too lazy to follow the link to the public document, here is a sample result: the good match between data and total predicted SM processes (including internal conversions!) is used to extract limits on SUSY models with R-parity violations, which can give rise to these signatures even in the absence of large missing transverse energy. You can see one such limit on the right: the black curve divides the parameter space into an excluded (left) and allowed (right) region, depending on the value of the squark and gluino masses. 




Comments