Today I wish to bring to your attention a figure recently obtained by the CDF collaboration, one which really tells a thousand words. Before I describe it to you, however, I would like to discuss at an elementary level a few basic concepts of particle theory which the figure well summarizes.


A Crash Course on Feynman Graphs


Let us start with a few elements on Feynman graphs -the diagrams that physicists use to draw on their blackboards to picture what really happens when particles react, and that actually enable the computation of the probability of those processes.

All particle reactions at a subnuclear level can be thought as the combination of basic elements: space-time lines describing particle propagation. If one takes the horizontal direction in a sheet of paper as that along which time flows, and the vertical direction as the one describing space separation between points, then a particle at rest can be described as a horizontal line. Of course: the particle is not moving in space, so its vertical coordinate remains fixed, while time flows, drawing a line from left to right in our sheet of paper. I am sure you do not actually need me to include here a figure with a straight line, do you ?

Now, a particle moving in some space direction may instead be drawn as a diagonal line, going upwards or downwards: as time flows from left to right, space (the vertical position) also changes. One can then picture the collision between two particles as their joining in the same space coordinate: as time flows they near each other, until they arrive at the same space point at a certain time instant. The diagram on the left describes the merging (annihilation) of the two particles into a third object -which might or might not be of the same kind as its parents (only gluon pairs can do the trick of fusing into one, but that is a detail for another post). The one on the right, however, pictures a particle splitting (decaying) into a pair of other bodies, which later travel in opposite directions, separating from each other.

You have now all the elements to understand what happens in the diagram pictured below, which in hadronic collisions describe the process called Drell-Yan: the annihilation of a quark-antiquark pair (the incoming lines on the left, which originally belonged to two colliding hadrons hA and hB) into a photon or Z boson, which later decays into a pair of charged leptons (the outgoing lines on the right).



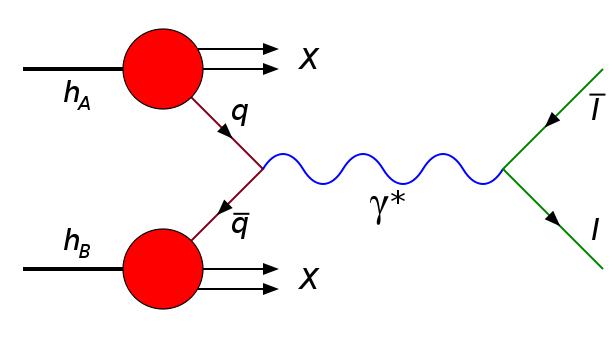
Enter Initial and Final State Radiation

All particle lines in a Feynman diagram have to be thought of as an abstraction: an elementary particle is a restless thing, which constantly interacts with the surrounding medium. Take an electron for instance: it constantly exchanges quanta of radiation with the electromagnetic field it is sitting in. These "virtual photons" emitted or absorbed are like a cloud surrounding the charge, and they are the means by which the medium feels the electron as much as the means by which the electron interacts with the medium.

We cannot picture all the virtual photons that are emitted or absorbed by an electron line. But we know how to write a single emission: a photon line departs from the electron, which changes its motion and decreases its energy. Such a "single quantum emission" is certainly again an abstraction -or, more precisely, an approximation. In cases when the emitted photon is a real one (which is when it does not get reabsorbed immediately by another particle, but merrily leaves the scene), and it has a sufficiently large energy, we can think of detecting the photon in our apparatus. So, imagine you are collecting Drell-Yan events by selecting events with two leptons of opposite charge and whose four-momenta add up to the Z boson mass: in a few -very few, but not zero- of those events, you expect to also see a energetic photon.

The process you are focusing on is then called "associated Z-gamma production", and it is a rare one indeed -only few dozens such events per week are created by the collisions recorded by CDF. Now, Z-gamma events may be of two different kinds: the photon may have been emitted by one of the two leptons materialized by the Z decay -and in that case we call it "final-state radiation", or FSR for insiders-, or it may have been emitted by one of the two quarks before they annihilated! Quarks, like electrons or muons, also carry electric charge, and they emit and absorb photons almost as readily as leptons. In the case of a quark emission we speak of "initial-state radiation" (ISR).

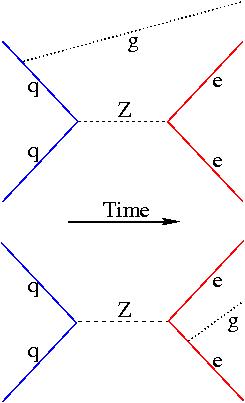From a diagrammatic point of view, there is not much difference between initial- and final-state radiation: check it out in the diagrams on the left. Basically, it all boils down to attaching a leg to one of the two quarks on the left (ISR) or to one of the leptons on the right (FSR).

What you cannot do, however, is attach the photon directly to the Z boson line: the Z boson is not electrically charged, and so it just does not know how to absorb, or emit, a photon. If this were not the case, we would have to rewrite the Standard Model -we would have discovered anomalous gauge boson couplings! In fact, the data displayed in the figure at the bottom of this article has been indeed used to constrain anomalous gauge couplings matching a Z and a photon line.

Now, the very nice thing about Z-gamma production is that, contrarily to what we experience with most other particle reactions, we have a very simple way of telling whether the photon was coming from a quark (ISR) or a lepton (FSR): final-state radiation is betrayed by the fact that the lepton emitting the photon loses energy, and thus when we use its energy to compute the Z mass, we find a smaller value! The photon has stolen some of the energy produced in the Z decay.

On the contrary, initial-state-radiation photons are sort of quantistic benefactors: it is through their emission that one of the two colliding quarks tunes its energy to get exactly the amount needed to "resonate" at the Z mass with the antiquark it is about to hit! What this means is that the photon can have any energy -this is only determined by the energy possessed by the emitting quark before the collision- and the Z will still have a chance to be created with its regular 91 GeV of mass.


The Plot, and why you should love it


Now I believe you have a chance to fully appreciate the figure below. It is a scatterplot: we call that way two-dimensional distributions, where each event is represented by a marker on the plane; in this case, red crosses stand for electron-positron events, and blue circles for muon pair events. On the horizontal axis of this figure, CDF puts the invariant mass of the two leptons; on the vertical axis, the total mass of the two leptons AND the photon is shown instead.

What do you expect to see for a ISR event ? Well, for it the Z mass computed with the two leptons evaluates correctly at 91 GeV (give or take a few -the imperfect match is due to the fact that lepton energies are measured with some approximation, and to the fact that the Z boson has a "finite width", a fact which I will not discuss in detail here); if one adds the initial state photon, instead, one obtains a large mass, because the photon carries at least a few GeV of additional energy. So one expects to see a vertical line of points at the horizontal abscissa of 91, with coordinates of 91 GeV or more.

And what for a FSR event ? The dilepton mass of a FSR event will fail to reach the Z mass value, because of the few GeV of energy stolen by the photon; but the lepton-lepton-photon mass will restore the balance and indeed add up to 91 GeV. So one in that case expects a horizontal scatter of points, whose abscissa has any value from 0 to 91 GeV, and vertical height always equal to 91 GeV.

Besides the two fuzzy horizontal and vertical lines, one does expect to see additional odd events scattered around the upper left half of the figure: they are due to events where the Z is not produced on its "mass shell". For sure, however, no event is expected in the lower right, because the dilepton plus photon mass is always larger than the dilepton mass alone.



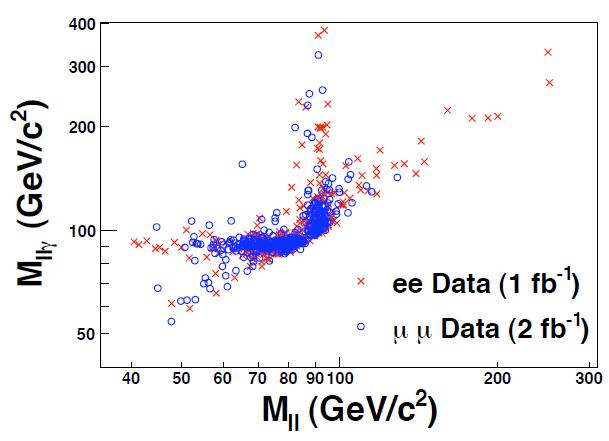
The above populations are exactly what you see in the figure. The ISR and FSR processes are caught pants down: they are recognized without doubt, for once proving that even subnuclear reactions have, in some cases, a well-determined identity.

In closing this piece, I wish to congratulate to the Duke group, which performed the search for these events and analyzed them: congratulations to Alfred Goshaw, Thomas Phillips, Janrong Deng, and Max Goncharov. Nicely done, guys.