When you find a Z candidate together with a photon as the outcome of the energetic collision of a proton and an antiproton, you are facing two quite different possibilities for the process which originated the pair: the photon may have been emitted from the quarks present in the initial state, or from the leptons present in the final state. Of course: only charged particles can emit photons, so in the Standard Model the Z cannot. (For simplicity, I am deliberately avoiding to consider "higher-order" quantum processes, which provide additional means by which a energetic photon can arise).
The "initial state" of a hadronic collision is constituted by the two colliding bodies, considered before the hard interaction takes place. The "final state" is instead composed by the particles created in the hard interaction. Since the "hard process" we are considering is Z-boson production, the initial state is composed by a quark-antiquark pair of the same flavour and same colour; the final state is instead composed by the muon pair (say) into which the Z decays.
The figure I posted is extremely interesting to me because it provides us with a clear distinction of the two quantum processes (emission of a hard photon by a fermionic line), based on the observed kinematics of the three reconstructed objects -muon pair and photon- we detect. On the horizontal axis what is plotted is the invariant mass of the muon pair; on the vertical axis is instead plotted the invariant mass of the three-body system.
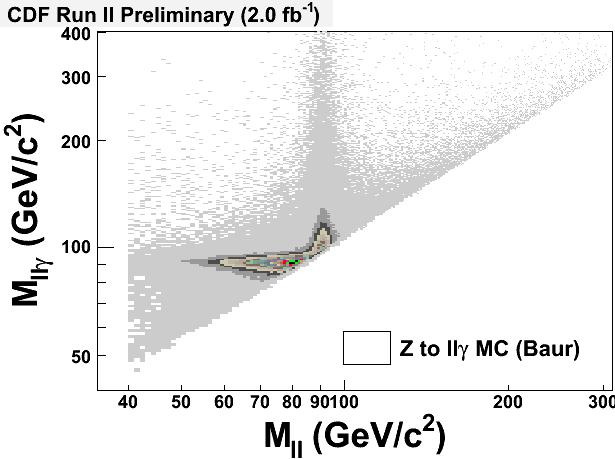
The axis labels are back in place in the version of the figure shown again above. From it, you realize that the dimuon mass is often sitting at 91 GeV or so -give or take a few GeV because of the small measurement errors of muon momenta: these events populate the vertical band, because the two muons make out the Z boson by themselves, and when you add the photon contribution you get a three-body mass which is higher. However, in a non negligible fraction of the times, the dimuon mass comes out much smaller: these events populate the horizontal band, and here you see that it is the three-body mass which sits at 91 GeV!
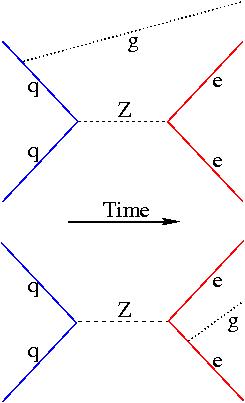It emerges that the vertical band is populated by "initial state radiation" events: the Z is a honest-to-god 91 GeV resonance, all of its mass turning into muon energies, and the photon is an addition: in a way it does not "belong" , so the three-body mass is higher than 91 GeV. A Feynman diagram of this process is shown in the top portion of the figure on the right ("g" labels the photon, which emerges from the initial state quark line shown in blue; here the Z decays to an electron-positron pair, the red line).Instead, the horizontal band shows events where the photon comes from the muons: only by adding it to the energy-momentum of the pair, can we get back the Z mass. These are "final-state radiation" events, described by the diagram shown in the bottom half of the figure on the right. Here the "g" is emitted by the red line.
Finally, the figure shows also a underlying "continuum" of low-rate events where the distinction is not so clear: these are events where multiple photon emission took place, or where the two muons come from a "off-shell" Z boson or virtual photon, the so-called "Drell-Yan" continuum. Stuff worth another post.
The figure object of the riddle has been crafted with a simulation program written by Ulrich Baur, a fine theorist who unfortunately died a few months ago. So this post and the previous question are a tribute to him. I had the pleasure to meet him in person and work with him for a study of Tevatron Run II sensitivities to electroweak radiative processes, and he struck me as a particularly well-mannered, pleasant person. He is surely missed.
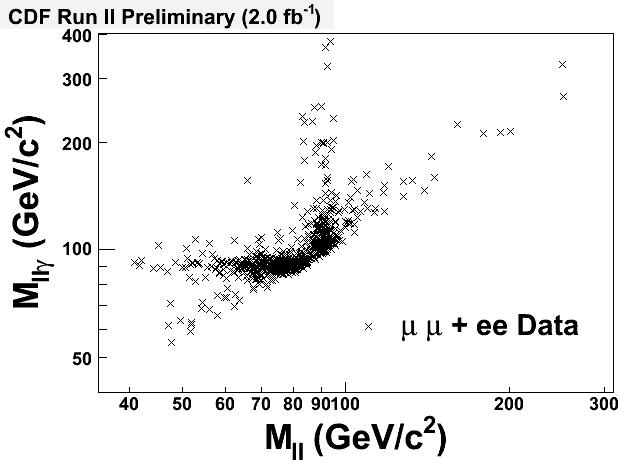
Now, with all the data that the Tevatron delivered in Run II, we have the luxury of comparing the prediction of Baur simulation with real Z-gamma candidates collected by CDF. Look at the figure below: the agreement with the simulated one is impressive.
Comments