The paper is quite technical and a detailed discussion of its content does not belong here. However, given the importance of its results, I wish to provide with a short summary those among you too lazy to download the paper.
 The authors consider the effect of Next-to-Next-to-Leading order (NNLO) corrections to the process of Higgs boson production by gluon-gluon fusion at a hadron collider (as in the graph shown here: a triangular loop of top quarks "connects" the gluons to the Higgs), followed by the decay of the Higgs to two W bosons.
The authors consider the effect of Next-to-Next-to-Leading order (NNLO) corrections to the process of Higgs boson production by gluon-gluon fusion at a hadron collider (as in the graph shown here: a triangular loop of top quarks "connects" the gluons to the Higgs), followed by the decay of the Higgs to two W bosons.That is exactly the process which has been used recently (together with a dozen of other less constraining ones) by the CDF and DZERO experiments at the Tevatron to exclude the existence of the Higgs boson in the mass region between 160 and 170 GeV, where the Higgs boson in fact decays preferentially to W boson pairs. For the distracted among you, below I show the recent Tevatron limits and an quick-and-dirty explanation of the figure.
 The figure above shows, as a function of the Higgs boson mass (on the horizontal axis), the 95% CL limit obtained by the Tevatron experiments, once they combined the results of all their Higgs searches. The full black line shows the actual limit, while the dashed one (surrounded by 1- and 2-sigma bands) shows the expected sensitivity of the experiments. The pink band on the left shows what mass range of the Higgs boson has been excluded in the past by the LEP II experiments at CERN, while the one on the right is the Tevatron exclusion region. The vertical axis has units of the "times the Standard Model" limits: an exclusion at, say, 5 times the SM for a mass of 130 GeV implies that a Higgs boson production with a rate five times higher than what the Standard Model predicts is excluded by the experiment; an exclusion of 1.0 or less means that Standard Model Higgs boson is ruled out in the corresponding mass range.
The figure above shows, as a function of the Higgs boson mass (on the horizontal axis), the 95% CL limit obtained by the Tevatron experiments, once they combined the results of all their Higgs searches. The full black line shows the actual limit, while the dashed one (surrounded by 1- and 2-sigma bands) shows the expected sensitivity of the experiments. The pink band on the left shows what mass range of the Higgs boson has been excluded in the past by the LEP II experiments at CERN, while the one on the right is the Tevatron exclusion region. The vertical axis has units of the "times the Standard Model" limits: an exclusion at, say, 5 times the SM for a mass of 130 GeV implies that a Higgs boson production with a rate five times higher than what the Standard Model predicts is excluded by the experiment; an exclusion of 1.0 or less means that Standard Model Higgs boson is ruled out in the corresponding mass range. NNLO corrections may have an impact in the computed acceptance of selection cuts that the experiments use to pre-select the sample where they search for the Higgs signal, as well as on the shape of the kinematical distributions which are used to compute a global discriminant with Artificial Neural Networks.
These tools are relatively new in data analysis of particle physics experiments, and many old dogs show scepticism when confronted with results obtained with them. One of the most principled objections that are usually cast is, in fact, the unknown dependence of the results on shape variations due to higher-order corrections on signal production.
The paper must be praised for its direct attack of these issues, and for the effort that the authors have put to bridge the gap between theoretical calculations and actual distributions and numbers which are needed as input by experimental measurements. It is not common to see a theoretical paper getting down to not just estimating the effect of higher-order terms on a cross-section, but computing the shape and normalization differences of a Neural Network output!
Indeed, the CDF and DZERO analyses are kept as a reference point, and the effect of the QCD corrections is ascertained by comparing the NNLO calculations to the modeling made by the experiments, which use a Monte Carlo simulation and rescale the absolute normalization with the use of so-called "K factors", mysterious-looking entities which are nothing but multiplicative factors by which experimentalists rescale their Monte Carlo predictions.
Surprisingly, the results are very good news for CDF and DZERO, and for those who root for the Tevatron in the hunt for the Higgs boson. In fact, it appears that the overall effect of the corrections is an increased acceptance to Higgs bosons of the data selection and of the Neural Network analysis. The latter, it must be stressed, is just an example, since it is very difficult to reproduce in detail the procedure used by the experiments; still, it is a very good approximation to the way the data is analyzed, and it appears that the results obtained by the theoretical study apply also to the results of the experiments.
Let me quote the paper:
To the best of our knowledge, so far there has been no study of how the distributions of ANN outputs are modified at higher orders in perturbation theory. Here we present for the first time an ANN output distribution, computed at fixed order in perturbation theory, beyond the leading order.
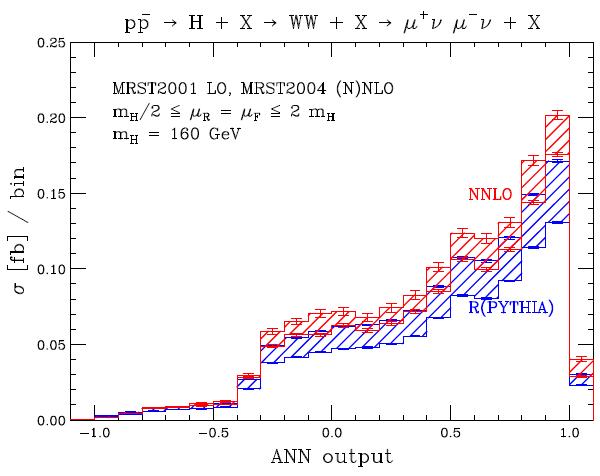
[...]in Fig. 9 we compare the ANN distribution obtained at NNLO QCD and with PYTHIA. We see that PYTHIA, even after rescaling with an inclusive K-factor, yields predictions which are smaller by 12-20%, depending on the chosen bin. This difference can be traced back to the difference in efficiency already observed at the level of the selection cuts placed on the kinematic input distributions.
Figure 9 is shown below. I cannot describe in detail the input of the neural network that the authors have used to generate this output shape; they are kinematical distributions obtained at generator level (i.e., without any detector effect factored in). With that in mind, we observe that the NNLO-computed cross section (in red) is always above the one computed by PYTHIA (in blue) over all the NN output range. The shape is instead in very good agreement.
The authors conclude as follows:
[...]we find that the acceptance computed with PYTHIA is between 12% and 21% smaller than the NNLO acceptance, depending on the choice of the factorization and renormalization scale. This result is not significantly altered by hadronization and underlying event and appears instead to be related to the matrix element and parton shower implementation in PYTHIA itself. Since the Tevatron analyses are based on PYTHIA, we believe that this effect could be important and requires a more detailed investigation within the framework of the full experimental analysis.
Now, what does this imply for the Tevatron limits on the Higgs boson ? Of course, if a limit on the existence of the Higgs boson is computed by NOT observing a certain number of signal events in the NN distribution, the limit becomes stronger if one finds out that the Standard Model actually predicts more signal. So we conclude that the Tevatron results are actually conservative, and their power of exclusion is slightly stronger.
I believe both CDF and DZERO will use the results of this theoretical study in their future results of Higgs boson searches. One simple way to do it is switching from PYTHIA, the Monte Carlo simulation they have been using, to HERWIG or MCatNLO, which are shown to be more in line with NNLO calculations.




Comments