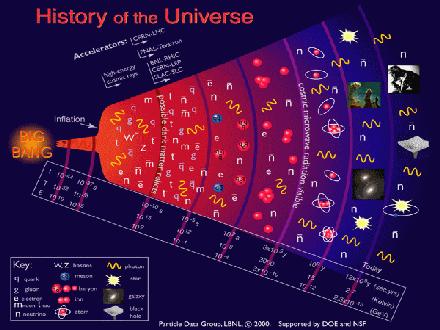
 A never ending story
A never ending storyThe history of the cosmos. In quaternionic physics one equation plays a major role. It is a mixture...
 The hierarchy of objects
The hierarchy of objectsI present you my personal view on the hierarchy of objects that occur in nature. I only treat the...
 Flat Quantum Physics
Flat Quantum PhysicsQuantum physics uses a parameter space that is curved. It is possible to cure this situation by...
 Ziggs, QPAD’s, curvature and inertia
Ziggs, QPAD’s, curvature and inertiaRecently Leonard Susskind introduced a new type of objects and called them ziggs.See: http://www...




