This is a question which was asked recently on quora: Is it possible to have a moon so reflective that when it reflects the light of the sun, it will be as if it is daylight? Anyway it is a rather fun problem, easy to work out by "back of the envelope calculations", and the answer takes us to some interesting areas of planetary physics.
First it would be easy to arrange for this by mega engineering if we had a Moon as big as our Earth. Cover the near hemisphere with mirrors and angle the mirrors so that they reflect almost all the sunlight received on that hemisphere towards the Earth at midnight. Then we would get as much sunlight as midnight as we do at midday and the full Moon at midnight would be as bright as the sun.
The more interesting question is, what about natural moons not covered in mirrors like this. Could a natural Moon be as bright as the sun? How bright can it be?
So, let's see, we can work this out from the albedo of the Moon, and the intensity of moonlight.
Best to use the geometric albedo here, so we can compare with a disk of same apparent diameter.
LET'S TRY VENUS
So, our Moon has a geometric albedo of 0.12. And Venus has a geometric albedo of 0.67
So suppose for instance that we had Venus orbiting where the Moon is.
Moon's diameter 3,476 kilometers
Venus diameter 12,104 kilometers.
BTW I have done all these equations in a form which lets you copy / paste them into Google to use it as a calculator.
So visual disk is increased in area by (12,104/3,476)^2 and the albedo increased by 0.67/0.12. So the strength of the moonlight is increased by (12,104/3,476)^2*(0.67/0.12) or about 68 times.
HOW MUCH DO WE NEED TO INCREASE THE BRIGHTNESS OF THE MOON?
Sadly that's not enough to make much of a difference, because moonlight is about 0.1 lux, up to 0.26 lux at the tropics - see Moonlight and sunlight is 32,000 lux upwards to 100,000 Lux
So we need to increase the intensity of the moonlight 385,000 times to get full moonlight in the tropics as bright as direct sunlight.
Venus would be 0.26*(12,104/3,476)^2*(0.67/0.12) or 17.6 lux. Compare 40 lux for typical indoor lighting of a home.
In all this we are not taking account of radiation in other wavelengths, just visible light.
HOW BIG SHOULD OUR PLANET BE THEN?
So how big would Venus need to be to do the trick? Well as Venus light was 19 times brighter than the Moon, then it needs to be about 2,000 times brighter very roughly. Or about 44 times larger in diameter.
Jupiter is only 12 times larger than Venus in diameter, and it has a lower geometric albedo than Venus. So it's not going to work to use Jupiter at the distance of the Moon. But let's do the calculation anyway and see how bright it would be.
Of course by now, we are a moon of Jupiter rather than the other way around. We would be orbiting Jupiter.
LET'S TRY JUPITER
Let's try Jupiter at distance of the Moon.
Albedo 0.52 (from Geometric albedo)
Diameter 142,984 km
So our calculation now is 0.26*(142,984/3,476)^2*(0.52/0.12) or 1,906 lux.
That's as bright as an overcast day, or studio lighting. So we are getting there.
To make it brighter, we can bring Jupiter closer to Earth. The area goes up as inverse square of distance.
So, let's see how close Jupiter would need to be to Earth to have same illumination as the sun.
ROCHE LIMIT
The Roche limit (for "fluid" satellites) is
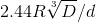(D = density of parent, d = density of satellite)
Or as an equation you can paste into google: 2.44 R (D/d)^(1/3)
Any satellite that orbits within the Roche limit is torn apart by tides (probably to form a ring system).
So - if its density is similar to Earth, then it can't orbit it closer than 2.44 times its radius.
Jupiter however has a density of only 1.33 g/cm³ and Earth's is 5.51 g/cm³ so Earth can orbit rather closer than that without getting torn apart by tides
Earth could orbit 2.44*69,911 (1.33/5.51)^(1/3) or 106,210 kms from Jupiter. We'd be orbiting it closer than Metis. Would be seriously tidally stretched but Earth would survive as a planet.
For closely orbiting planets, it's not accurate enough to just estimate the increase in brightness using the inverse square of the distance.
We need to use the area subtended by a sphere. The exact formula is that the solid angle is 2 * PI * (1-sqrt(r^2 - R^2)/r) for r > R where r is the distance from the center of the planet and R is is radius. See Solid angles subtended by rotary solids at a point.
So we need to use the ratios of the solid angles at 106,210 km and at 405,400 km. Using that formula, then it's brightness is 1906*2 * Pi * (1-sqrt( 106,210^2 - 69,911^2)/106,210)/( 2 * Pi * (1-sqrt(405,400^2 - 69,911^2)/405,400))
Or, 31,448 lux
And if it had the same surface brightness as Venus, then it would be (0.67/0.52)*31,448 or about 40,500 lux.
TYPICAL DAY ON EARTH TIDALLY LOCKED AND CLOSELY ORBITING A SUPER JUPITER IN ITS SKY
If you lived on the Super Jupiter facing side, you'd get this sequence, starting from midday:
1. Midday. Super Jupiter is not visible in the sky because it is in "new moon phase" . But around midday every day, you'd get a long eclipse with the sun hidden behind Super Jupiter. So that would be the only time of darkness in the day. That's when you'd be able to see the stars and other moons though with a big black patch in the sky in the direction of the Super Jupiter.
2, As the sun sets, Super Jupiter catches the sunlight and gets brighter. When the sun dips below the horizon Jupiter is at first quarter.
3, At midnight you get "full Super Jupiter" (every "night") - but as midnight approaches, the shadow of the Earth would move across Jupiter and at midnight this shadow would be directly overhead. So, you'd get a dip in brightness at midnight itself. Though the edges of the Super Jupiter itself would still be bright around the horizon as our shadow only shades a small spot in the center
4. Then after that the Super Jupiter wanes and the sun rises.
With that whole cycle repeating every hour and seventeen minutes and no darkness at all.
On the other side of the Earth facing away from Super Jupiter, you would get no light from our Super Jupiter at all. It just gets a 12 hour day with normal sunlight sun rising and setting.
What about a larger more distant planet?
LARGEST EXOPLANET - LET'S TRY WASP-17b
Here is the largest exoplanet discovered
WASP-17b
It's 1.991 times the radius of Jupiter (so roughly 140,000 km).
It's density is 0.486 times the density of Jupiter so 0.486*1.33.
Earth's density d is 5.51 g/cm³
It's radius is 1.991*69,911 = 139,192 kilometers, diameter, 278,385 km
So it's Roche limit for Earth is 2.44 * 1.991*69,911 * (0.486*1.33/5.51)^(1/3)
=339,630 kms.
So, coincidentally, a little less than the distance of the Moon. So we could orbit WASP-17b at the same distance as the Moon and not be torn apart, if I've got these numbers right.
So that makes the calculation easy. Let's just leave it at the Moon's distance for simplicity.
Only thing is I don't know its geometrical albedo - probably could calculate that from its distance and magnitude. But meanwhile let's just suppose it is same as Venus. Then we get it's brightness at distance of the Moon as 0.26*(2* 1.991*69,911/3,476)^2*(0.6/0.12)
or about 8,338 Lux So that's about the same brightness as full daylight but not direct sunlight, brighter than an overcast day. Radiometry and photometry in astronomy
So - that's actually not as bright as a close orbit around Jupiter. On the other hand it is probably safer, less likely to be fried by fierce electromagnetic radiation perhaps.
Visual diameter (278,385 /3,476)*0.5 or about 40 degrees.
So it would fill a large part of the sky. If we bring it a little closer, to the Roche limit, then its 8,338*(405,400/339,630)^2 or about 11,900 lux
Coincidentally it's diameter is roughly the same as the diameter of Saturn's ring system.
The last image in this sequence gives an idea of what it would be like to replace our Moon by the largest known exoplanet. Imagine a planet as wide in diameter as Saturn is in this video, and you've got it.
RINGED PLANET
It could be brighter still if it had rings. And those would have no effect on its Roche limit.
Only problem then is though, that our orbit would most likely be in the ring plane. So we wouldn't get much sunlight reflected. It would help though if we were on a ring crossing orbit say perpendicular to the rings.
I've been trying to find figures on how much Saturn brightens depending on its tilt - does anyone know?
If it was like this giant ring system, though, 200 times larger than Saturn it might have a larger effect:
This is an artist's impression of the giant ring system Super-Saturn J1407b - "Super Saturn" Has an Enormous Ring System and Maybe Even Exomoons - 200 times larger than Saturn's ring system, 120 million kilometers Super-Saturn J1407b Hosts Massive Ring System, Astronomers Say
However this is a very young system in process of forming satellites, its sun is just 16 millions years old. Faraway planet J1407b is lord of the rings. So the rings will probably dissipate as the moons form.
GRAVITATIONALLY LOCKED BINARY PLANET
(Image NASA) Are Habitable Binary Planets Possible? : DNews - 'Double Earths' Could Be Fun Exoplanets To Hunt For -- If They Exist
see: Can binary terrestrial planets exist?
Explored fictionally in Robert Forward's "Rocheworld"
Rocheworld
If the two planets are gravitationally locked to each other, in the same way as Pluto and Charon, then the tidal effects no longer matter.
They are just permanently distorted. You can even have an Earth sized planet almost touching our Earth - even with a shared atmosphere and ocean in principle
We don't know any contact binary planets, but many contact binary stars are known, and including "overcontact binaries" that are so close together that their atmospheres overlap - the first discovered W Ursae Majoris.
from: Chapter 19-7
see Contact Binaries
So the "Roche world" scenario certainly seems physically possible.
So in that case, well forget about all those limitations. It could be as big as Jupiter and only 69,911 kms away, except that Earth would be seriously tidally stretched. If we and Jupiter are tidally locked, then no problem.
In a contact or over contact binary, then if you lived close to the contact point, the other planet would fill your sky. On the other hand then at midnight, if it was orbiting in the same plane as your orbit around the sun, then the shadow of Earth pass across our sister world which would make the sky darker in the center. And at midday then it would eclipse the sun.
The calculations would get more complicated to figure it out exactly - how bright it would be at all times of the day at various distances from the contact point. For instance if you lived right at the contact point, you'd only see the sun at sunrise and sunset, and the rest of the time it would be hidden behind both planets, and whichever planet it wasn't illuminating would be in eclipse.
So then you'd only get light around the horizon and your only illumination would be at "night" when the sun would illuminate the opposite planet around the horizon.
So someone would need to do a proper detailed analysis of this. But it seems likely that with the other planet filling your sky, there would be places close to the contact point and times of day when it was as bright at night as it is in the daytime.
A PLANET THAT LIGHT'S UP ITS OWN SKY
It's possible in principle to get a planet that takes up non convex shapes, if it spins fast enough. If so then you might get your planet appearing in its own sky.
If it's an overcontact binary, then in a way both are the "same planet" so that's an example.
If a planet spins fast enough, it can take many different shapes theoretically, including a donut shaped planet. See Surprising Shapes for Rapidly Spinning Planets.
So, though it may seem unlikely, still, doesn't seem you can rule out a donut shaped planet. (Or for that matter maybe such a planet created artificially by some ETI with mega technology)
If you lived near the hole in the donut in a donut shaped Earth you'd get a lot of reflected light from the planet itself
And it could have moons also adding to the brightness:
Just mentioning it for completeness. As we don't know of any planets shaped like this and it would probably need very rare and unusual conditions to create one, perhaps we can leave it for now.
Anders Sandberg's fun article explores many aspects of life on a donut shaped planet - and the orbits of satellites and moons around such a planet.
What would the Earth be like if it was the shape of a donut?
See also Surprising Shapes for Rapidly Spinning Planets
HABITABLE ZONE
So anyway that's an interesting thought. What about a moon orbiting a big gas giant just outside the habitable zone. Or a Roche World contact or over contact binary for inhabitants living near the contact point?
Or what about a planet orbiting a gas giant with a large and dense ring system?
It would need more careful calculation. Not just the maximum brightness at midnight or close to, but the total amount of light received throughout the night from it's parent planet.
But I think that could possibly double the total amount of sunlight it receives in the day. I wonder if that extends the habitable zone outwards for closely orbiting Earth sized moons of gas giants and gas giants with rings? Or indeed for Roche world type binary planets also to some extent? I think it would.
COMMENT IF YOU FIND ANY MISTAKES
This is just a first rough calculation, if you spot any mistakes in this calculation do say!
Also does anyone know of any articles or papers on this. Has anyone explored the variations in illumination of points on a Roche world close to the contact point? Or for Earth sized moons orbiting close to gas giants with rings like Saturn?
Or if you have any other ideas or suggestions for ways that a natural Moon could be as bright as the sun.
See also Surprising Shapes for Rapidly Spinning Planets and Can Moons Have Moonlets? Or Rings? Moonlets Of Pluto's Moons?
KINDLE BOOKSHELF
I have made some of my blog posts into booklets for kindle, so you can download them and read off-line, formatted as books, with table of contents etc.
Check out my kindle bookshelf.
You can get this and many more of my answers now as a kindle book:
Comments