This is a commonly used argument, indeed often taken for granted. We can simulate physics on a computer. So, the argument goes, what is to stop us eventually simulating your whole body including your brain? And if so, is it not just a matter of time, and increasing computer power before we have exact simulations of humans as computer programs? Programs whose behaviour is indistinguishable from humans?
This is a staple of many science fiction stories of course. But some logicians, philosophers and physicists think there are flaws in this argument.
We know the laws of physics are incomplete. Could there be physical processes which for some reason are impossible to simulate using a computer program? And could processes like that go on in a human being?
This is what Roger Penrose thinks.
Roger Penrose, professor at Oxford university and theoretician in quantum gravity - who gave detailed arguments for the view that human brains can't be simulated with a programmable computer.
Author of "The Emperor's New Mind" and "Shadows of the Mind" and other publications where he explores these ideas.
His work follows on from work by Kurt Gödel himself
Kurt Gödel who proved the famous "incompleteness theorems" showing that maths can never be completely described in a fixed set of axioms and deduction rules - he thought that humans could not be simulated using finitely programmable machines.
He explores these philosophical ideas in "Some basic theorems on the foundations of mathematics and their implications" -
Then later by the philosopher John Lucas who also thinks that human understanding of maths can't be reduced to the actions of a finitely describable computer program.
John Lucas, author of ‘Minds, Machines and Gödel’, in which he argues that an automaton cannot represent a human mathematician.
The main thing Roger Penrose contributed, as a quantum physicist, was to suggest possibilities for physical processes involved in the brain that might be impossible to simulate in a computer program - and to present a much more detailed argument from Gödel's result to his conclusions.
If he is right, then it is never going to be possible to create "digital humans" as computer programs. But it's much more general than that. If he is right, it is not just impossible to completely simulate a human down to every atom in a computer - you can't even have a computer program that can truly understand addition and multiplication in the way a human can.
I'm not going to talk so much here about his arguments in detail. This article is more of a "What if". What are the implications if he turns out to be right? Whatever you think about the actual arguments used for the conclusions?
It's a philosophical debate that's been going on for over 60 years now, with no sign of a consensus, so it is not likely to be resolved definitively one way or the other any time soon. I will briefly touch on the arguments themselves also, but just enough to give a flavour of what it's all about.
SIMPLE SEEMING TASKS THAT CAN'T BE SIMULATED BY A COMPUTER PROGRAM
This claim is not as wild as it might seem because there are some quite simple seeming tasks that can't be simulated by a computer program. The one all the arguments here focus on is, recognizing mathematical truths.
You might think it was easy enough to program a computer to prove the same things a human can prove, for instance about numbers. To check our proofs and come up with new proofs of its own.
HUMAN "OUT OF THE BOX" THINKING
But turns out - that it's harder than you think. You can set out a simple set of axioms and deduction rules - but the thing is that humans can always "think out of the box" and that out of the box thinking lets you see that some things have to be true, which a computer program caught in the box of those rules you wrote down can never find out.
By "out of the box" here - I mean in a simple general way - something that everyone does.
Children as well as adults ask "Why is the sky blue?" "Why do clouds float"? "Is there an end to space?". "Where am I in the universe?" "Why is there anywhere at all?". It is as natural for a human to do this "out of the box" thinking as it is to breathe.
For a computer program to ask questions like that, then you have to program those questions into it. And it would never ask any questions about its own programming unless you program the ability to ask those questions also. Program it to add and multiply - and it will never ask any questions about the rules you program it to follow unless you program it to do that also.
And - it's not enough to make a program that is self modifying - that also has limits because at some level you have to specify how it does its self modifications - and that then puts limits on its creativity, it is still incapable of "out of the box thinking" about its own self modification rules.
I thought I'd say a bit more about this as in some of the online discussions of this article, readers seem to think that self modifying programs get around this argument. But they don't get you out of the box at all. I've indented this so you can skip this if it is already obvious for you.
Why can't a programmed self modifying program get "out of the box"?
The thing is - that so long as the self modifications themselves are programmed - you can always simulate it using another program that doesn't modify itself. It's basically an "interpreter" for the first program.
This new program, let's call it B, treats the first program, A, as data, and then it runs it following its instructions in whatever programming language A is written in - so you have to program an interpreter into B. And if the program A modifies itself in the middle of its calculations, then all B has to do is modify the program code in the data.
In this way you can push all the self modifying behaviour into the data - so long as the modifications themselves are programmed. B itself is never modified. You end up with a single program + data and that's all there is. So the self modifying vanishes, introduces nothing essentially new to the discussion.
To duplicate this "out of the box" thinking that humans are always capable of, a program needs to be endlessly creative adding new axioms and continually tweaking its program in a way that can never itself be programmed.
That's basically what Gödel proved in his first incompleteness theorem.
So - that's a kind of plausibility argument that no finite computer program can understand truth in the way a human does, because all such programs are limited in some way. Given that maths can never be completely described by a finite set of axioms - how could there be some similar limit on what humans can see to be true?
I'm not saying yet that this is rigorous. But - irrespective of whether we can make this into a rigorous, watertight argument - what if it turns out that the conclusion is true?
This happens all the time in maths. When you try to prove something, your first few attempts may fail - but still - that doesn't mean at all that your conclusion is false.
So, what if there is indeed some non computable process going on here, when humans understand mathematical truth (or indeed, any kind of a truth)?
What would that say about physics and artificial intelligence?
POTENTIAL FOR PHYSICS THAT WE DON'T KNOW ABOUT WITHIN LIVING CREATURES
Of course this is no use if you think that we already fully understand all the laws of physics that are going on at the level of living creatures. Because then our behaviour would still be capable of a computer simulation no matter what we think is going on.
You might think at first, that the only scope for new fundamental physics would be in the likes of black holes, neutron stars, and the like, or high speed particle collisions such as the LHC, ultra low or ultra high temperatures and so on.
But - some physicists think there may also be new physics at a more ordinary level. For instance, some think that this could happen whenever you have enough mass interacting - a Planck's mass worth (about 1019 times the mass of a proton, it's 21.767 micrograms) - that's around the same as the mass of a human eyelash.
Measure the mass of an eyelash with a DIY microbalance
Enthusiast measures human eyelash at about 35 micrograms. The Planck mass - amount of mass needed for "spontaneous gravitational collapse" is 21.767 micrograms, so around the same mass as an eyelash.
Roger Penrose thinks that as soon as you have as much mass as this in an indeterminate state - that it has to "collapse" - has to "make up its mind" where it is - and that when that happens, he thinks something non computable happens, something that can't be simulated with a computer program.
This suggestions comes as a result of the problem of an observer in quantum mechanics. This is the idea that everything is somewhat fluid until you observe it. An electron can be in a "superposition of many states" until you make an "observation" - and then when that happens then it "collapses" into a single state.
In the classical "two slit" experiment, if you observe which of two slits an electron goes through, it always goes through one or the other. But if instead you look to see where it hits a screen, the other side of the two slits - then repeat this experiment many times, you get a diffraction pattern effect, that can only be explained by saying that all the electrons go through both of them at once.
So - who or what is it that does this "observation" that collapses the electron into some particular state? There is no properly accepted explanation in quantum mechanics, and possibly if we get an answer to this, it might take us into new physics.
There are many ways of attempting to solve it.
ORCHESTRATED REDUCTION - ROGER PENROSE'S IDEA
Roger Penrose's idea - shared by other quantum physicists - is that you get a spontaneous collapse whenever the mass of interacting particles is large enough. This makes it an example of an objective collapse theory for quantum mechanics.
So in this case then by observing the electron we couple the entire mass of ourselves, experimental apparatus etc to the state of the electron - which then forces it to go into one or other state.
Then his idea is that this objective collapse is what lets the non computable physics enters in. This objective collapse would be something new that isn't predicted or explained in standard Quantum Mechanics.
If our brains were just quantum computers, they would still be Turing machines - just very fast ones, because quantum computers with entangled qubits can be shown to be equivalent to Turing machines. All they do is to reduce the complexity of some tasks so that they can be carried out more quickly, with fewer steps.
However, this objective collapse introduces something new. It means that the entangled particles collapse into some particular state at a time when according to classical QM theory no observations are going on.
If that happens - then there would need to be new physics to explain in detail how, and when, this collapse happens - and what leads to it collapsing one way rather than another. This then could be something that is going on all the time, quite ordinary - not in neutron stars or black holes or particle accelerators - that we don't yet understand.
HOW MUCH MASS IS NEEDED FOR THIS PROPOSED NON COMPUTABLE OBJECTIVE COLLAPSE?
Then - the amount of matter needed for this objective collapse - it could be anything. What if you have to be say, a kilogram in mass for it to happen? But physicists have picked on this particular amount of mass, the Planck's mass, about the same as a human eyelash, as a likely figure.
The Planck's mass is the amount of matter needed to form a mini black hole, if you compressed all that matter to a single point. So - as best I understand it - the idea is that - when you get enough matter involved in superposition of states so that if it was all in one point it would form the tiniest possible mini black hole - a Planck particle to be more precise - at that point some "decision" has to be made about where it is. So you get a spontaneous collapse into one of the numerous possible states, and this is the part of the process where something non computable would enter in through the interaction of gravity with quantum mechanics.
(BTW physicists think that a Planck particle can probably only last for a fraction of a second before disintegrating due to Hawkings radiation. And of course the chance of this actually happening in ordinary situations is so low as to be for all practical purposes zero. But whether or not, this collapse would, in theory, briefly cut it off from communication with the rest of the universe and so the possibility of it happening could force a decision about what state the matter is in).
Then the particles start interacting together again until you get another Planck's mass of interacting matter - at which point it has to collapse again and so it continues.
Roger Penrose proposes to tie this to quantum superpositions going on inside neurons - and also quantum states spanning several neurons - to explain how the brain is able to go beyond the limitations of computable physics.
More particularly he ties it to quantum superposition in microtubules - these are tiny structures within individual neurons (which you also get in other types of cell as well). He thinks that an individual neuron is vastly more complicated in the way it works than a simple "neural net node" and plays a more important role in our thinking than the simplified "neurons" of neural nets.
Staining of microtubules in a cell fixed by means of anti -beta - tubulin antibodies
There's some evidence that these microtubules are not just structural but involved in the cell's decision making.
Roger Penrose and Stuart Hameroff's idea is that this network of microtubules within each neuron is also involved in our thought and consciousness. Then the idea is that the brain structure and the connections between neurons then leads to quantum correlations between these networks in other neurons right across the brain.
If they are right, the brain could be quite a few orders of magnitude more complicated than most AI researchers think - and with the processes going at such a small scale, at the atomic level, then there is plenty of scope for new physics to be involved.
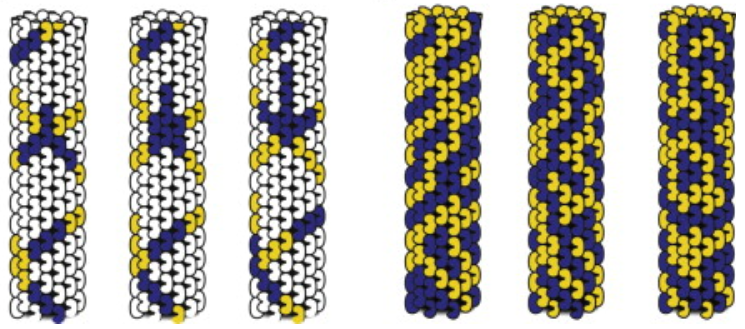
These patterns show how microtubules may engage in some form of "computation" using processes similar to the way cellular automata like Conway's game of life work.
It is a controversial theory. First, it's based on the idea of objective collapse which is just a theory at present which we are a long way from being able to verify or disprove, when we can't yet even entangle more than a few qubits, never mind 1019 of them.
Also, at first many thought that it was impossible that there could be any large scale quantum processes going on in warm conditions such as our brains. But - there is a fair amount of evidence now of different types of "warm quantum effects". See for instance Evidence that photosynthesis efficiency is based on quantum mechanics - it seems that plants in some way or other "try all possible paths" to find the most efficient way to do photosynthesis.
Then there is emerging evidence that quantum effects are also important for the ways that birds can navigate using the Earth's magnetic field, because they get confused by radio signals and weak coloured light which should have no effect. Also for the human sense of smell.
See Quantum biology: Do weird physics effects abound in nature? (BBC)
And then, quantum superposition has also been detected in the microtubules themselves, as predicted by his theory.
For the latest on their theory, a paper they wrote earlier this year lead to several news stories: see Discovery of quantum vibrations in microtubules inside brain neurons corroborates controversial 20-year-old theory of consciousness and Discovery of quantum vibrations in 'microtubules' inside brain neurons supports controversial theory of consciousness
This is not the only way that new physics could arise on the ordinary level of the human brain, though. I don't think the idea of non computable physics in the brain should stand or fall depending on whether Orchestrated Reduction is confirmed or disproved. It's just one way it could happen.
It could be that we just don't know enough yet to work out the physics of what is going on. Maybe it doesn't even involve quantum mechanics, maybe something else.
PLAUSIBILITY ARGUMENT - THAT OUR NEURONS MUST AT LEAST BE MORE COMPLEX THAN "NEURAL NET" NODES
Recently there was a news story: "Supercomputer models one second of human brain activity" about a super computer that modeled a neural net thought to be as complex as the human brain in terms of the number of neurons. It took it forty minutes to simulate one second of neural activity.
However, a single cell creature such as an amoeba moves around, has complex decisions to make, do I go here or there, eats food etc.
Amoeba Eating - and rejecting food
If you modeled the behaviour of an amoeba with a neural net you would need thousands of neurons. But it doesn't have any.
So - this is just a plausibility argument - it's not proof.
But - if our brains were as simple as these neural nets suggest - then a creature with a single neuron that takes advantage of its internal structure would be easily outsmarted by another creature with a brain with many thousands of neurons which it treats as just nodes in a neural net.
NOBODY HAS PROVED THAT ALL THE LAWS OF PHYSICS ARE COMPUTABLE
Whether or not you think Roger Penrose has succeeded in this proof - certainly nobody has proved in the other direction that all the laws of physics have to be computable. So - until someone comes up with a totally convincing proof either way, we are free to take either possibility as a hypothesis. There is no a priori reason to suppose that all physics has to be computable. So, let's start there, by looking at the consequences of non computable physics, and especially non computable processes going on in us.
SO, WHAT IF THIS IS RIGHT, THAT THERE ARE NON COMPUTABLE PHYSICAL PROCESSES GOING ON IN LIVING ORGANISMS?
The first consequence would be, that we will never simulate physics completely with a programmable computer machine.
That includes also,
- Quantum computers if they act according to the currently known laws of physics with entangled qbits
- Hardware neural nets (if they can be simulated in an ordinary computer as software neural nets)
- Self modifying computer programs
- Machines that use probabilistic methods to solve things (e.g. probabilistic annealing),
- Massively parallel computers with billions of processors acting in parallel.
- Hardware cellular automata
All of those have been shown to be logically equivalent to a Turing machine and can't introduce anything essentially new. All they can do is to speed things up, make our computers faster.
To get an idea of whether some kind of computer introduces anything essentially new here - ask yourself - "Could this computer itself be simulated with a normal linear type computer program, even if it can only be simulated very slowly?"
So for instance, here is a simulation of a 3D cellular automaton. The next state of each cell depends on its neighbours in the previous frame. You could build this as a hardware cellular automaton with millions of individual chips behaving like this and running in parallel. Or you can simulate the whole thing in a non parallel computer. The non parallel computer is much slower, but it behaves exactly the same way. So this introduces nothing new.
Example of a 3D Cellular automata.
If we can simulate any of these types of computer in another computer already proved to be equivalent to a Turing machine in this way, then it doesn't introduce anything non computable, by definition.
So - the first consequence would be, that none of those types of computers would be able to completely simulate the workings of a human being.
COMPUTER PROGRAMS CAN STILL BE BETTER AT MANY TASKS THAN HUMANS
Obviously computers are better at calculations. They can also beat humans at chess, now, since Deep Blue won against Kasporov. And may in the future be better at driving cars than us. We may rely on them more and more for various aspects of our lives.
A Ride in the Google Self Driving Car.
But the computer program that beats you at chess has no idea what chess is, or what a chess piece is. It couldn't discuss the match with you, or recognize a chess game in a photograph. It doesn't understand anything. All it can do is follow instructions.
The program that drives your self driving car has no idea what a pedestrian is really, it's just a particular type of pattern. Still, you can program it to work well in a human environment, through endless tweaking of the program and feedback from human test drivers in the car. And maybe one day the self driving cars will be better at driving than humans, so much so that we let them drive our cars for us so that we have far fewer accidents.
Our programs so far are good at many things, and far better at us at quite a few things, but I think fair to say, that they don't really "understand" anything in the way that humans understand them.
If Roger Penrose is right, then no programmable computer can ever understand mathematical truth. If so - perhaps arguably they can never really understand anything at all, just follow the instructions programmed into them.
WHAT DOES NON COMPUTABLE MEAN HERE
It might help to have an example of some non computable functions. Because it is easy to think that our computers can simulate everything, if we can just make them fast enough. That's not true though.
There are many problems in maths that our computers have no hope at all of solving, because they are non computable problems.
A simple example is to calculate the tiling function. This is a function that given any finite set of square tiles, with various indentations around the sides that constrain how they fit together - tells you a value k for the largest k by k square pattern of tiles it can tile, or returns, say, 0 if it can tile the entire plane.
Or simpler - just to answer yes, or no, does this set of tiles tile the entire plane?
At first sight you might think it is likely to be quite easy to answer a question like that. Most times, when you tile a region - you have some repeating unit. So just try larger and larger patches of tiles until you either find a repeating unit, or find you can't go any further. You might think that would be a simple program that would be guaranteed to give you an answer if you search long enough for any given set of tiles.
But it's not as easy as it seems because of the discovery of tiles that can tile the entire plane - but can only do it non periodically - i.e. without any repeating units.
Here is Roger Penrose standing on a floor made following one of his tilings. As you see there are two kinds of rhomb there - a fat one and a thin one. What you don't see there are the matching rules that force them to go in particular patterns.

So, you mark the two rhombs like that, with those notches - which force the curves to continue across the boundaries of the tiles. It turns out that when you do that - then you can't tile the plane with a repeating block of tiles - no matter how large. But you can tile it to infinity, in a non periodic way.
Tony Smith's stunning image showing how the Penrose tiles tile to infinity. Though the various patches of tiles appear over and over again in the pattern - the whole thing doesn't repeat. It's because of the possibility of non repeating tilings like this that the tiling problem is so intractable. So much so that it is non computable - no computer program can solve it.
It's existence of tiling patterns like this that makes it so hard to tell if a set of tiles will tile the plane or not.
And indeed - mathematicians proved that no computer program can ever be written that will, given a set of tiles, tell you if it will tile the plane or not.
That includes quantum computers, artificial neural nets, and machines with finite states (e.g. binary, digital) that incorporate random processes. Anything equivalent to a Turing machine.
It's because of the existence of Wang tiles which can be used to simulate the behaviour of any Turing machine.
This makes the tiling problem computationally equivalent to the halting problem - the question - will a computer program halt or not? It is very easy to show that, given a program in any sufficiently flexible computer language, you can never write an automated program tester to answer the question "does this program halt or not?".
Because of that result, and because Wang tiles can simulate computations, it turns out that there is no computable function that, given a finite set of Wang tiles, can put any bounds on the size of the largest region it can tile.
That is to say - to make this clearer - if we know how to tile the plane we can get the computer to print out a tiling. And a computer program might well be able to solve many particular cases of Wang tiling problems.
But if some process in nature was able to take any arbitrary finite set of Wang Tiles as input - and give some output that tells us how to tile the plane - or the largest area that can be tiled if it can't tile the entire plane - that physical process would be something our computers can never simulate.
For more examples, see this discussion: Non-computable but easily described arithmetical functions
Gödel, Lucas and Penrose think that Gödel has proved, that when we understand mathematical truth we are making a non computable leap that our programmed computers will never be able to achieve.
By extension, when we understand truth at all, we are probably making a similar non computable leap. Mathematical truth is just easier to analyse, which is why they focus on it first.
IF SO A SPEED UP IS NOT ENOUGH
If it's true that we are doing something non computable when we understand mathematical truth, you can't solve non computable problems by a speed up.
Take the example of the task to write a computer program that
- Given a finite set of square Wang tiles with matching rules as input
- Will output a number k for the size of the largest k by k region of the plane that it can tile (and, say, output 0 if it tiles the plane to infinity).
We know that no Turing equivalent computer program can do this. So - if the problem you are tackling is one that is computationally insolvable, like this one, no amount of speed up, no amount of computer time, or disk space, can solve it.
. 
Example, my surface Pro tablet that I'm writing this on - it could solve exactly the same problems as the ones solved by the £97m weather supercomputer built by the Met office - only difference is, it would probably take centuries, or thousands of years even to do a few seconds worth of the simulation. But it is a Turing Computable problem, so, given enough time and if I give it enough disk space (so need to invest in some external USB drives probably), my tablet can solve it.
But if it is true that AI requires ability to tackle non computable problems - then - no ordinary Turing supercomputer can ever solve it, however fast, however much it reduces the complexities of tasks, however much it is optimised for the calculations it does.
CAN WE GO BEYOND THE TURING LIMIT WITH PRESENT DAY PHYSICS
Roger Penrose suggested that we need new physics to go beyond the Turing limit. But is there any chance that we can do this with present day physics?
If it is possible, it is likely to be very difficult.
Take for example, quantum computers using entangled qubits (of the classical type without Penrose's objective collapse). They are so different from ordinary computers, with superposition of states, and even have a different logic, quantum logic. It would have been entirely reasonable to assume that they would introduce something new, solve previously non computable problems. But - it turns out - that they are equivalent to Turing machines.
These quantum entangled qubit computers should make some problems less complex, and so, far easier to solve. But, as it turned out, they can't solve any new previously unsolvable problems.
This has happened time and again - that a new type of computer - either theoretical, or actual, is proved to be equivalent to a Turing machine.
ROBIN GANDY'S "GANDY MACHINES" ANALYSIS
There have been attempts to show that large classes of machines based on physics also have to be Turing machines. For instance Robin Gandy's 1980 paper on what came to be known as "Gandy Machines" (For later paper about his ideas, by other authors see "An abstract model for parallel computation: Gandy's Thesis)
He showed that if you have a machine with finitely many states, and finitely many ways to assemble them together, with limits to speed of light communication - and with a finite running time - then - you have is equivalent to a Turing machine.
He limits his discussion to Babbage computer type machines - mechanical devices that compute with discrete states.
Babbage Difference Engine in Motion
So - you might think that is rather limiting - but - apart from quantum computers, just about all present day computers are logically equivalent to Babbage type machines - the elecronics just makes them a lot faster but essentially they are doing the same thing that Babbage's machine did.
So his arguments apply to them also.
WHAT ABOUT RANDOM PROCESSES
So this is something that often comes up - can we not get around the whole issue by adding some randomness? Might this perhaps be how we manage to do our own "out of the box thinking"?
Well - if you are talking about randomizing between finitely many states - e.g. choose a number between 1 and 10, or randomly flip a few binary bits - this won't make any difference at all to computability.
That's because, given unlimited time, you can simply try out all the possibilities. Just see what would happen for all the different ways the random bits can be flipped.
This is what's known as a "Probabilistic Turing Machine".
Random methods are useful sometimes. For instance the process of Stochastic annealing
Traveling Salesman Problem Visualization - solved by simulated annealing
In this way probabilistic methods can sometimes solve problems more quickly than a more direct search. Still - when they work - they only give you a speed up. Don't let you solve a previously uncomputable problem like the Wang's tiling problem.
So long as you stay in the binary (or digital etc) realm, i.e. randomize discrete states, random methods don't let you solve any new, previously uncomputable problems.
WHAT KIND OF A COMPUTER COULD GET AROUND ROBIN GANDY'S ANALYSIS?
So - if some new architecture can get around his argument, it probably it can't be purely digital, with a finite number of states, but would need to be based on continuous, analogue type data, with theoretically infinitely many states (e.g. any point on the real line between 0 and 1 for instance).
You don't have to actually actualize all those states in the sense that anyone needs to be able to measure anything to infinitely many places of precision - but as calculations progress it approximates them more and more.
Actually some early computers were like this, continuous, analogue type machines. And there are ideas for future computers like this also.
If you used the word "computer" in 1950, this is what they would think you are talking about. It's not a programmed Babbage type mechanical computer - rather - is an analogue machine, doesn't use numbers internally at all. Skip to 1.26 to see the computer in action. Just a minute or two of it.
At 1:45 "If you look inside a computer, you find an impressive assembly of basic mechanisms. Some of them are duplicated many times in one computer"
Wikipedia article about it, range keeper.
Alternatively - if using quantum superposition - it needs to have no upper bound on the number of states a component can go into, or some such.
I don't think anyone has proved that it is impossible to solve non computable problems with present day physics.
Indeed, in a book called Neural Networks and Analog Computation: Beyond the Turing Limit (Progress in Theoretical Computer Science) - showed that perhaps hardware neural networks might, in some situations, be able to go beyond the Turing limit.
WHAT ABOUT BIOLOGICAL "COMPUTERS" AND COMPUTERS BASED ON PHYSICS WE DON'T UNDERSTAND YET?
What if we use actual biological neurons in our computers? There is already work underway on this, using biological neurons for computing.I don't think any simple neural net made of actual neurons in place of hardware neurons would do something non computable. But - what about use of actual neurons in future with better understanding of how they work and how they communicate, maybe based on Roger Penrose's theory or some other future version of it?
This goes back to 1999 - this computer is made out of neurons taken from leeches - and it can add up - a very primitive computer - the neurons are in a petri dish, each neuron represents a different number, and when connected together they can "add up".
Or slime moulds - there is research right now into using slime moulds for computers.
Computing with slime: Logical circuits built using living slime molds
Or - we might create a computer that we think is a quantum computer - but nobody is quite sure how it works. Indeed we have one of those already. The D-Wave Systems quantum computer.
Quantum Computing - D-Wave's quantum computer, which seems to work, and is very fast also, but nobody seems to be entirely clear how it works.
Nobody quite knows how it works, but it does seem to, in independent tests.
Now chances are it is just a quantum computer - so faster - but essentially doing the same sorts of things as ordinary programs can do - but massively multi-tasking basically.
But what if some future D-Wave systems type company constructs a computer that they think is a quantum computer - but instead it is operating according to whatever principles work in the human brain - some kind of underlying layer of operation that they don't understand, and didn't build in intentionally -but it is there and helps their computer work?
Such a machine, might, just possibly, be able to understand truth and falsity, and be in some way aware.
MORE THAN NON COMPUTABILITY NEEDED
Just triggering something non computable wouldn't be enough - hard though that is. It then has to start acting in a coherent sentient way. It is surely far more likely to be random, chaotic, or patterned in some way that is intricate, impossible to simulate in a computer program, but makes no sense.
So something more is needed, surely. But what?
Perhaps if we somehow come to learn how this works in the brain, maybe we can then apply that to make machine sentience?
Or maybe - somehow we could get there by simulating processes of evolution within our future non computable physics machines?
WHY "OUT OF THE BOX" THINKING PROBABLY CAN'T BE REDUCED TO ANY KIND OF INSTRUCTION FOLLOWING OR PROGRAM
The "Church-Turing thesis" hypothesizes that anything that any human (or computer) can do that is following a fixed set of instructions, can be done with a Turing machine.
That doesn't prevent us going beyond the Turing limit - because it specifically doesn't address "out of the box" type thinking. When Gödel proved his theorem he was not just following rules. He was inventing new rules to follow.
But - if this thesis is true - then it means that a computer or intelligence that goes beyond the Turing Limit can't be reduced to any form of rule following.
That also excludes self modifying programs too, as before, because a self modifying instruction following program, even if it changes its own instructions - it can be simulated using a fixed non self modifying instruction following program. That is so long as it is following rules about how to change the instructions it follows. So a self modifying instruction following program doesn't help at all.
AI BABIES - NOT FOLLOWING ANY SET OF INSTRUCTIONS
So, whatever method we use, if they use non computable physics - that means that, if the Church-Turing thesis is true, we can't reduce their operations to any kind of a computer program, any kind of a set of rules they are following.
It's not even like a neural net where we can program it to respond to particular inputs in a desired way by tweaking all the parameters inside it in an automatic feedback process - because that too is an approach within computable physics and programming.
This is the example of the "artificial intelligence baby".
One day, it "Wakes up" with an understanding of truth. But - what would our world be like to it?
UPLIFTED CREATURES
Another example of this could be the process of "uplift" as explored in David Brin's novels and his Uplift Universe.
Perhaps we will have the capability to do this at an earlier stage than the other ideas - as we don't need to really understand how the brain works or is organized in detail, or how DNA leads to the brain.
Instead the task is to figure out what in our DNA etc. leads to particular structures and features in the brain that let us understand speech (for instance) - and then find a way to modify their DNA etc to incorporate those into other animals such as dolphins.
In that way we could maybe end up with dolphins and other creatures able to speak, and understand human speech - without us ever truly understanding how this uplift process works, really, at the atomic level. Just that we have found out how to do it.
OUR AI BABY
So, if this was ever possible, I think it means that an AI, whether a computer based on non computable physics, or a neural net using actual neurons, or a slime mould computer, or an uplifted creature, would be more like a baby learning things for the first time, with no way to program "prior knowledge and understanding" into them. Because what is going on is something that can't be programmed.
So then, that raises major ethical dilemmas. If we do manage to create physical systems that can truly "understand truth" - then I think when they "wake up" they will be confused and not understand how to make sense of their situation.
Even if we don't build the equivalent of pain receptors into their systems (and we might well, especially if they are mobile, in order to help them respond to things likely to damage them) - they will have this idea of truth, and falsity - and a wish to know what is true. And that then will lead also to frustration - how do you know what is true and what isn't? So we would be creating a creature that can suffer. So we have a responsibility to it.
UPLIFT BABIES
Same also with uplift - if you modify say a dolphin, so that it can understand human speech - and communicate with us.
It's got a head start on a computer program - a dolphin already, I'd say, "understands its world" that it lives in - it knows what other dolphins are, what food is, what the sea is, in some sense it "knows things". If humans "truly understand" things - then dolphins also - and indeed other living creatures, even dogs, even ants, in a way - they are not just following a program, but, they are relating to things, in some sense they understand things, if in a dim way compared to ourselves. They understand e.g. what is food, they have friends, they know things about their world that they live in.
When you know things, then, I would say, that's a form of understanding of truth.
So, I don't think a dolphin needs to be "uplifted" to understand truth. But if you then modify its DNA and biology so it can speak to humans and understand as we do - and have similar capabilities to us - you end up with a creature that is part dolphin part human in its intelligence. And it's going to have many problems - though as well - maybe many insights as well.
ETHICAL RESPONSIBILITIES TO OUR AI BABIES
So - not saying we shouldn't do this ever. Or that we have to do it either. This is a decision for future generations probably.
But if we do - it's again like having a baby - we would have a responsibility to the uplifted creatures, just as to the AIs and can expect them to have a difficult time as they mature and try to make sense of the world they are born into.
In David Brin's novels then the ETs that uplift other creatures speak for them and have responsibilities towards them in the galactic community. I imagine that it would be a bit like that - in the future, species that have been uplifted will know which species did the uplifting (usually), maybe even who within the species did this, and will have - hopefully, some gratitude, hopefully they are pleased that they got uplifted.
But their "species parents", as it were, will also have responsibilities towards them as well.
AI AND UPLIFT BABIES GROWING UP
Seems unlikely to me, that, e.g. a program designed to drive cars, or play chess or whatever, would somehow suddenly "wake up" and understand the world like a human being. Or even one designed as a generalist, say as a companion for humans or a personal robot "butler" as in some of Asimov's stories, or the like. Because of Penrose's and Gödel's arguments.
They will be programmed machines, and will have whatever capabilities we build into them - and if the designer has any sense, then as the robots get more powerful then you build in safeguards also so that it is easy to stop them instantly if they cause any problems through some problem with the way they interact with the world.
And the sorts of problems I imagine happening are - like the issues with rapid stock trading using programs that respond to share prices - due to capabilities that we build in to the computer that then have unfortunate unexpected side effects.
But as for the true artificial intelligences, if we do manage to give birth to these "AI babies" as a civilization - then also bring them to maturity - then they are our responsibility also, to give them as good an upbringing as we can. Just as with parents and children, some of our ideas and values will end up influencing them. But also - they'll be influenced by the whole civilization they grow up in.
If they have a problematical upbringing then they could become problematical AI adults - just the same as with humans.
If this ever happens we'd have got to know them well at this stage, and them us. And developed mutual trust (hopefully).
And if brought up well, then they may be valuable parts of our society as adults. And - hopefully if there are many of them they can help each other to mature as well, as some of them reach adult hood, they may help their less mature "newborns".
A COMPUTER PROGRAM COULD NEVER REALLY UNDERSTAND ADDITION AND MULTIPLICATION - IF PENROSE, LUCAS AND GÖDEL ARE RIGHT
The maths we are talking about here need not involve abstract difficult to understand concepts. Gödel proved his result for one of our simplest theories with just a few axioms, the axioms of elementary number theory.
Then later, it was found out that you can manage with an even simpler theory. All you need to have is an axiom system powerful enough to be able to add 1 to any number, has a 0, and lets you define addition and multiplication.
This tiny system of arithmetic makes your mathematical proofs cumbersome - still - it's enough for Gödel's results.
For the mathematicians amongst you, here are the actual axioms, of Robinson's Arithmetic - one of the simplest axiom systems of the type that Penrose and the others are talking about.
It's an axiomatization of the positive numbers (no negative numbers or fractions), and it goes
1. You can't get to 0 by adding 1 to any other number
2. If x+1 = y+1 then x = y
3. Every number other than 0 can be got by adding 1 to another number
4. x+0 = x
5. x + (y+1) = (x + y)+1
6. x*0 = 0
7. x * (y+1) = x*y + x
There, axioms 1 tells you what 0 is, and 2 to 3 tell you how the successor operation, of adding 1 works. Axioms 4 and 5 tell you how addition works, and axioms 5 and 6 tell you how multiplication works.
Amazingly - this alone, plus ordinary rules of "first order logic" so you can say things like "There exists x..." or "For all x ..." and use logical deduction - is enough to be beyond the grasp of our computer program, according to Penrose, and Gödel indeed.
A program would have no trouble at all checking proofs that it can carry out with those 7 axioms, and proving new results.
But - turns out - that humans can look at this list of axioms and come up with new results about the numbers by reasoning "about the axioms and proof methods " - and a computer program programmed just with these axioms simply can't make that deductive leap and see that those things are true.
So in that sense, it doesn't really understand the axiom system, it is just following rules.
So, I'd say, that though the program can add and multiply - it doesn't really, truly, understand addition and multiplication in the way a human being does. It has no idea, really, what it is doing when it adds numbers together, it is just following rules. Otherwise, it would surely be able, with enough time and thought, to follow through the implications and see the truth of Gödel's sentence.
This is a general result for any theory that is rich enough to do Gödel's proof construction. It doesn't have to have numbers in it as such, so long as we can find something in it that we can reinterpret as numbers.
SOME THEORIES SUCH AS EUCLIDEAN GEOMETRY ARE COMPLETE AND DECIDABLE
Now this result is not true of all theories. Ordinary ("first order") Euclidean geometry is an example of a theory that is complete and decidable. It is a rich and complex theory - but not quite complex enough so that we can interpret arithmetic within it.
So - we could write a computer program to explore Euclidean geometry - and though "out of the box" thinking would help it to find shortcuts to proofs of the results - still, anything we can prove as humans can be put into a proof that our computer program can understand.
BUT YOU DON'T NEED ACTUAL NUMBERS, IN AN OBVIOUS SENSE, BUILT INTO THE AXIOMS
But once you have anything resembling numbers with addition and multiplication - then these "out of the box" Gödel sentences arise.
It doesn't have to have numbers in the theory in an obvious sense. An example is the theory of "hereditarily finite sets" - the theory that results if you take the axioms of set theory and remove the infinity axiom.
This is a theory that only talks about the empty set (set with no members) and then ways you can combine sets together.
| 0 | = {} | |
| 1 | = { 0 } | = { {} } |
| 2 | = { 0, 1 } | = { {}, {{}} } |
| 3 | = { 0, 1, 2 } | = { {}, {{}}, {{},{{}}} } |
| 4 | = { 0, 1, 2, 3 } | = { {}, {{}}, {{},{{}}}, {{},{{}},{{},{{}}}} } |
Even in this simple theory, you have something that works like numbers, the Von Neumann ordinals. You start with the empty set as your "zero". Then the set whose only member is the empty set, that's your "1" as it has only one member. Then the set whose members are all the sets defined so far - it's got two members so is your "2". Then repeat the process to get "3", "4" etc.
You can then define addition and multiplication using set operations - and you find that even though there is nothing resembling a number in your list of axioms, still you have these things you can interpret as numbers, and that's all you need - you can build a Gödel sentence using these instead.
See Gödel's Incompleteness Theorems (Stanford University of Philosophy).
RECOMMEND STANFORD ENCYCLOPEDIA FOR PHILOSOPHY OF MATHS
Note - that if you want to find out more about philosophy of maths - I would recommend the Stanford Encyclopedia of Philosophy- it is far far better than Wikipedia in this area.
Wikipedia is often an excellent source for formal logic.
But when it comes to philosophy of logic and philosophy of mathematics - and for that matter the incompleteness theorems the Stanford Encyclopedia is currently far better, and Wikipedia tends to have inaccuracies as well. I expect this will change as Wikipedia improves - but - I think it's likely to be one of the harder areas for Wikipedia to cover.
SKETCH OF WHAT HUMANS CAN FIND OUT
I thought I'd give just the briefest of sketches of Gödel's argument, but won't go into details at all and will skip over the most difficult part of his proof altogether. If you want an entertaining popular exposition of this, try Douglas Hoffstadter's Gödel Escher Bach, and Endless Golden Braid.
Title cover of Douglas Hoffstadter's book, good popular account of Gödel's result.
Gödel found a way to represent proofs, and theorems, as numbers within the theory. Let's just put them in single quotes, so 'q' is the number that encodes the theorem or proof q.
That's not so hard to understand nowadays. The text I'm writing just now is stored in the computer, not as letters, but as numbers. And - if I write out a proof, and then save that to a file - the file itself could be encoded into a single large number, easily, in many ways.
Then - using various mathematical tricks, he managed to find a complicated arithmetical expression, let's call it ProvableArith('q'), a statement about the number 'q' just involving additions, multiplications, variables and logic.
ProvableArith() here is a single, very complex arithmetical statement about numbers. It says nothing about proofs directly, but a human mathematician can see that it is true if, and only if, the statement encoded as 'q', our original q has a proof in our theory.
So far this is straightforward. To actually construct his statement, which I'm calling ProvableArith, and to prove it works as required involves a lot of work, it's a major part of his original paper - and it involves some tricky maths - but the basic idea is easy to understand.
His next step is the most outstandingly clever and original part of his paper.
Here the maths gets really hard, and I will just skip it. It's not at all obvious that you can do this - but he manages by using clever mathematical tricks to show that you can always find an arithmetical expression
G
which is only true if ProvablArith('G') is false.
It's important I think to realize - that here G doesn't actually say in the axiom system, or indeed in any language, that our arithmetical statement "ProvableArith('G') is false". It is just some complex arithmetical expression that we, as mathematicians, can see has the value true if ProvableArith('G') has the value false, and the value false, if ProvableArith('G') has the value true.
And what's more you can actually show this equivalence within your theory. The only thing you can't do within the formal theory is to do the "out of the box thinking" to understand the implications of what you just proved.
I won't go into the details here - it is hard to explain it well, and the details don't matter here. For mathematicians and logicians, see Gödel's Incompleteness Theorems (Stanford University of Philosophy).
So - you can show in this rigorous way, that G is true if and only if it is not provable within the theory.
But then - going one step further - if it was provable in the theory - then it would be false, and what's more our theory would be plain inconsistent. By inspecting the proof and converting it into its Gödel number - you'd be able to come up with a particular, very large number that was a counter example to G. Then you would also have your original proof of G, within the theory, so combing the two together, you would be able to derive a contradiction within the theory.
So - if our theory is consistent - and there are good reasons for supposing that arithmetic is consistent (though we can never prove it) - then G can't have a proof from the axioms. And so therefore it has to be true.
In this way - a human can see that certain things are true that no computer program, programmed with just the axioms and deduction rules of that theory could deduce.
WHAT IF WE ADD IN THE NEGATION OF G?
Now, you could say - that, so what? We don't need an actual example of a proof of G, to add in the negation of G as an axiom. We end up with a rather paradoxical theory - it is "omega inconsistent". The negation of G - at least in classical logic, says that there is a number 'p' that codes up a proof of G from the remaining axioms - when we already know by that no particular number can ever code up a proof of that type.
So we've added an axiom saying that a particular type of number exists, when we already know that there can never be any number with those properties. A theory like that is called "omega inconsistent" (omega is a mathematical symbol for the order type of a simple infinite sequence).
Still - there is nothing saying you can't built an "omega inconsistent" theory like that.
We can even work with inconsistent theories in paraconsistent logic.
So does it matter if the computer can't "see" that G is true? Is it really "true" in any absolute sense if we can consistently (but omega inconsistently) add in the axiom that it is false?
THAT DOESN'T MAKE ANY DIFFERENCE TO THE ARGUMENT HOWEVER
Well - that is beside the point here. The thing is - that our computer program, when presented with these proofs that we have come up with - if it doesn't have the additional understanding needed to understand Gödel's proof - won't be able to deduce anything about G.
It can't deduce that it can add in the negation of G and get an omega inconsistent but consistent theory. It can't deduce either that it can add in G and get a theory that is both consistent and omega consistent.
As far as the computer program is concerned, our G is just a complicated arithmetical statement which it hasn't yet proved or disproved.
And for the program - yes - it is true only if Provable('G') is false - but our computer program interprets " Provable('G')" here as just a complicated statement of numbers - so what? Doesn't mean anything of significance to it, just said that 'G' which it doesn't connect with G, is a number with some complicated properties.
So - however you interpret it - still humans understand something here that the program never can
WHAT IF YOU ADD IN THE GÖDEL SENTENCE PROOF METHODS
Now, you could program in all these leaps of deduction that a human can make - program in the rules for making a Gödel encoding and mapping formulae to numbers and proving Gödel sentences - but that doesn't help
That's because, it turns out that whatever program you write like that - it just gives you a more complex axiom system for your computer to follow - and you can then find new results that it can't recognize within that axiom system.
And what's more - we aren't talking about abstract abstruse or questionable areas of maths (such as the "Large Cardinality Axioms" for maths geeks). We are just talking about ordinary arithmetic -a very intricate sentence, but basically it's not talking about anything more complicated or abstract than you do when you say that - for instance, there are infinitely many primes. Or indeed, just, that the numbers go on for ever.
Also another thing to bear in mind here - at what point, as we add more and more of these extra Gödel methods, sometimes perhaps also various undending sequences of such methods - at what point does the computer finally "understand" addition and multiplication so it can be said to understand mathematical truth?
With humans - if you explain addition and multiplication - at some point you "get it" - you don't even need a formal set of axioms to do that. And those seven axioms would be fine, or the Peano axioms. No need to add in all the other Gödel methods for us to understand their implications, and to follow through the reasoning, given time and patience.
But a computer program can't "get it" at all with just these few axioms.
GÖDEL'S OWN TAKE ON IT
Gödel's argument is not particularly convincing - and he says as much himself, but it shows that he thought himself that probably human minds can't be reduced to a finite machine (i.e. Turing Machine).
He looked instead at diophantine problems - simultaneous polynomial equations in several unknowns with only integer solutions. His result showed that no finite system of axioms and deduction rules is sufficient to solve all diophantine equations. In this quote, by "absolutely unsolvable" he means - not solvable by any human being.
"So the following disjunctive conclusion is inevitable: Either mathematics is incompletable in this sense, that its evident axioms can never be comprised in a finite rule, that is to say, the human mind (even within the realm of pure mathematics) infinitely surpasses the powers of any finite machine, or else there exist absolutely unsolvable diophantine problems of the type specified"
He goes on to say that he finds the first of these two possibilities more plausible. See "Some basic theorems on the foundations of mathematics and their implications" - lots of missing pages in the preview, sorry.
The main difference is that Roger Penrose took this a lot further, applied it to physics, and supplied what he considered to be a proof that human minds can't be reduced to a program, using ideas of Turing machines combined with Gödel's results.
Gödel died in 1978, so there is no way to know what he would make of Penrose's argument.
PENROSE'S ARGUMENT
He presents a complex argument, and there are many details that need to be considered carefully. Have a read of his two books, The Emperor's New Mind (the entire book is available to read online as a google book) , and Shadows of the Mind for the details.
So, I'm not going to attempt to present his actual arguments here in any detail at all.
But the essence of it is that
- It is impossible for a Turing machine to enumerate all possible Gödel sentences. Such a program will always have a Gödel sentence derivable from its program which it can never discover
- Humans have no problem discovering these sentences and seeing the truth of them
So, therefore humans are not reducible to Turing machines
Here is a thoughtful essay by John Lucas, where he comments on the follow up discussion of Roger Penrose's ideas. The Gödelian Argument: Turn Over the Page
Also - Gödel had platonist, maybe dualist ideas about mind and matter. While Roger Penrose is approaching this very much as a physicist, as a problem in physics, how can humans brains understand maths, when maths is not within the grasp of any computer program?
OBJECTIONS TO LUCAS'S AND PENROSE'S ARGUMENT
One simple objection made early on, is to say - that humans are also limited, there are things we can't assert too.
Take for instance the sentence
"Lucas can't assert the truth of this statement"
That sentence is true, but John Lucas can't say that it is true.
or more generally
"I can't assert the truth of this statement"
- that's a sentence that applies to all of us. Nobody can assert that it is true - nevertheless seems that in some sense it is true.
A variation on the argument was brought up by Daryl McCullough in "Can Humans Escape Gödel? " where he uses a similar sentence "This sentence is not an unassailable belief of Roger Penrose."
However - Roger Penrose has answered this already. These are sentences in natural language, and we know that we run into difficulties in logic if we use unrestricted natural language.
However they don't seem to be problems with understanding maths as such. Especially such a simple area as number theory.
The thing is, that Gödel's sentence - though it's construction was inspired by these sentences, is not in itself paradoxical. Indeed it is just a rather intricate expression about ordinary arithmetic involving nothing more complex than addition and multiplication - and what's more a sentence in a simple axiom system that we believe to be consistent.
So we are talking about a sentence about arithmetic that a human mathematician can see to be true, which the original computer program can't see to be true.
PENROSE'S "P SENTENCES"
To make this clearer - he uses a technical trick, to let him talk in a perfectly general way about mathematical truth - but to avoid all the problems of natural languages.
But this can be a bit confusing if you don't realize why he does this.
He made it into an argument about "P sentences" - sentences that are true if and only if some particular Turing machine can never halt.
Statements about mathematics can be put in that form, and many natural language statements can also - lots of things can. But these self referring paradoxical sentences can't be put into that form.
It's a bit confusing because - earlier on he is talking about Turing machines as computer programs that some people think could be artificial intelligences. While here he is talking about them in a different way - as a technical device to simplify discussion of what counts as a mathematical truth.
Anyway - I think best not to get too bogged down in this here. It's a helpful distinction but only if you are well up on formal logic, Turing machines etc. I thought I'd mention it as it is something that comes up if you read the literature on the subject.
MAIN THING IS - THAT WE CAN DO MATHS EVEN THOUGH NATURAL LANGUAGE IS PRONE TO PARADOXES
But - doesn't matter quite how you do it, the main thing is that we can still do maths even though natural language is prone to paradoxes. And we do that by being especially careful about the language we use when we do maths.
So - if you then require that humans and the computer program keep to acceptable "mathematical language" - then you no longer need to take account of these kinds of sentences.
And then - it turns out - the computer program still has things it can't see to be true.
And these are truths in simple areas of maths such as arithmetic.
WHAT IF WE HUMANS ARE ALSO LIMITED IN THE SAME WAY
But - what if we do have a Gödel sentence ourselves also - but don't know it?
Most of the objections to his arguments are along these lines in one way or another. I.e. accept that the Gödel sentences are true, and that every computer program does have such a sentence, that it can't see to be true - but they then argue, that we have sentences like that also, we just are not aware of them.
After all mathematicians make mistakes. But we are able to correct our mistakes.
And - we do get caught "in the box" of our thinking in many areas of thought. But - are any of these boxes absolute - ones that we can never escape, ever? And can this be the case in the area of pure maths?
Especially in an area of maths with the underlying simplicity of pure arithmetic with addition and multiplication only? Is it plausible that somehow there are truths in this field of elementary arithmetic that we can never, ever, see because we are caught in some kind of a mathematical box in our thinking that we can't escape?
Well - here the arguments get really intricate. Has he proved his case? Or is it logically possible that human beings also have "Gödel sentences" that we are not aware of?
You can read some of the many arguments and counter arguments here, this article by Roger Penrose answering some of the many criticisms of his work.
Beyond the Doubting of a Shadow, A Reply to Commentaries on Shadows of the Mind,
For the papers he cites and replies to, most of the links he gives there are now broken, but you can find the papers easily if you paste the links into the wayback machine. For instance, Can Physics Provide a Theory of Consciousness? by Barnard J. Bars, Penrose's Gödelian Argument by Solomon Feferman etc.
Here is Roger Penrose talking about it:
Sir Roger Penrose — The quantum nature of consciousness
And here he is with his colleague the biologist Stuart Hameroff. This interview is well worth listening, despite a bit of background noise.
Interview with Nobel prize candidate Sir Roger Penrose and Stuart Hameroff
WHETHER HE HAS PROVED HIS RESULT OR NOT
Whatever you think though, whether you think he has proved his case or not, nobody, surely, has yet proved the opposite position - that all physics including human behaviour, can be simulated in a computer.
I'm not sure why so many are so sure of that conclusion - that a computer program can simulate a human - when nobody has proved it or has any idea yet of how to prove it.
And - it seems at least to be a reasonable philosophical position for anyone to take, that the human mind is essentially non computable.
Myself anyway - I now expect that some time or another down the road, we will hit some truly non computable physics. Though whether in the form of Roger Penrose's Orch Or theory or some other idea - maybe not involving quantum mechanics at all - or even quantum gravity - I don't know.
It's interesting as an area of philosophy which leads to an actual prediction about the future of science. A clear prediction that computer programs will never fully emulate human beings, so long as they are based on physics as currently understood, or computer programs as we currently understand those.
And then based on Roger Penrose's ideas - I think it is reasonable also to say that it predicts non computable areas of physics.
Is there any other area of pure philosophy that leads to a future science prediction?
And that then leads to the idea that if we ever do have Artificial Intelligence then it is likely to be impossible to program, in some intrinsic way because at its core, it is in some way doing something essentially non computable. And, I think myself, that means that it would start off like a young thing or baby - or may be an "uplifted species" or similar.
What do you think?
If you like this article, you might also like my: Maths From An Extra Terrestrial Civilization - What Could It Be Like - And Would We Understand It?
Also Why Strong Artificial Intelligences Need Protection From Us - Not Us From Them













Comments