A few years back I heard Joy Christian give a talk on his disproof of Bell's theorem, where he explained his idea for an experiment involving two hemispheres with a mass stuck on each.

To me it seemed obvious that the first thing to do with such an idea was to write a computer simulation of it.

It took me some time to get round to it, and I was rather distracted on the way looking into computer game engines, but it is finally finished, and can be seen at http://tachyos.org/bell/bell1.html.  

The result is unsurprising:



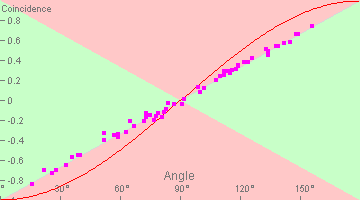
The green areas are those results allowed by Bell's theorem, the pink area those forbidden, and the red line is the experimental result from quantum theory. So the simulation doesn't disobey Bell's theorem.

In Bell's theorem it is assumed that the results of the measurement are single bits of information. If it were allowed to return a unit vector, then the measuring devices could ignore the properties of the object to be measured, and simply return results based on their settings, unit vectors a and -b. The correlation would be the dot product -a.b .Christian has the devices return the unit bivector valued results μa and - μb where μ (the hidden variable) is a unit trivector.

The product of these is -a.b - μa × b and if μ takes the values +I and -I equally often then the second term will average out to zero, so the result of this is just the same as using vector results.  Christian's claim is that because bivectors and scalars together form a subalgebra of the Clfford algebra - the quaternions - then bivector results are really just the same as scalar results. I'm not convinced.

 I only came across the explanation late in the project, and I was rather disappointed - if I'd have known about it to start with then I probably wouldn't have bothered doing the simulation.  Christian emphasises the importance of the global topology of the quaternions and their double cover of su(2), but in the end these play no part in the result.  Although I hadn't expected an actual disproof of Bell's theorem,    I had hoped for some insight into it.  Double covers can be tricky things.  For instance, suppose you could only count up to 3, and wanted to know what 2+2 was.  

Let y=2+2 .
Then (y-(3+3))(y-3)+(3×3)/(2×2)=-2×1+(3×3)/(2×2)=(3×3×3-2×2)/(2×2)=1/(2×2)

Putting this in terms of numbers we know

y²-9y+9/4 = 1/4 i.e. (y-9/2)²=(1/2)²

Hence Danger! Will Robinson Danger! Square root has a double cover

y-9/2 = 1/2 so y=5 i.e. 2+2=5

So it seemed entirely possible that the double cover would be the reason why Bell's theorem appeared to have been disproved.  Maybe this would have lead to some extra insight about the theorem - all this nonsensical talk about non-realistic models is getting rather stale. But it wasn't to be.

Further information about the results of the simulation can be found at http://quantropy.org/13/