Rocket science deserves its reputation as a difficult subject to approach. Relativistic rocket science is scarier still. If one tries to take this difficult, scary subject, and apply it to the way the biggest masses in all the Universe move, wouldn’t that be crazy? No, this idea is something that could get you certified. If you don’t know the difference between crazy and certified, well, neither did I before my 2 week vacation at Boulder Community Hospital. That story is too long to tell now.
[click or skip the reading of the content of this blog]


Newton’s law of gravity is broken. It has been broken since 1933. Frank Zwicky was trying to figure out the motions of a thousand identified galaxies in the Coma Cluster. The calculations did not go well. He could measure the light, guess the weight, and measure velocities. Put that all together with the viral theorem, and his calculations suggested we need more mass, like 400 times the visible mass. Oops.

The rotation of thin disk galaxies was not attempted until the early 1960s. Newton would not have done it since he didn't know about galaxies. Alar Toomre from MIT did the hard math using elliptical integrals to figure out the rotation profiles. The calculations did not go well. There was enough mass in the galaxies to get the stars moving at the maximum velocities seen, but not enough to keep them going at that speed. Oops.

There was another problem. If one gave a slight nudge to the galaxy along the axis of rotation, then the galaxies should collapse into a ball. Thin disc galaxy geometry is unstable to a gravitational bump from a passing nearby galaxy. Spiral galaxies would thus have trouble lasting for billions of years. Oops.

Classical big bang theory is based on a great volume of great data: everyone is running away from us. Those that are near us jog. Those farthest away sprint at speeds approaching that of light. Run it all in reverse, and in the past we were all closer. Go back farther in time, and we would get closer together. And closer. And closer. There must be a limit to this exercise, and it is called the Big Bang. The math relies on Newton’s law.

Two problems emerge. One is called the flatness problem. Gravity is all about acceleration. Go faster or slower young man! One stable solution is to go slow and then, like a frightened tortoise, revert back into the shell. Forget about a Universe lasting 13 billion years, it would never happen if the start were a wee bit slower. Another stable solution is to go too fast, the sprinting hare. This would be so fast as to skip forming galaxies. There is no stable solution between these two extremes. What we see, a flat Universe is mathematically an unstable solution. It is like balancing a pencil on its tip, only the classical big bang is much less likely than that. Oops.

The cosmic background radiation is the family photo from those early times. Everyone agreed on what velocity to go when leaving the Big Bang party. The horizon problem is that different parts of the Universe were spacelike separated from each other, and thus could not talk about what that speed should be. This was an exact agreement, at least to five significant digits. When parts of a system are independent, reaching a consensus is absurd. Oops.

Now consider now. Only gravity works on the scale of the entire Universe. Gravity is all about attraction, the force of universal love. That should slow down the sprint away from each other. Logic dictates one choice. Science as a practice demands data. This is not easy data to get. Until the measurement of the Hubble constant was nailed down, I am not sure if it was possible. They got the data, and the data says we are not slowing down as we should, we are speeding up. Oops.

These three problems have three hypotheses that have gain supporters. Dark matter hopes to supply the stuff needed to make the motion seen in galaxies work as well as make thing stable. Inflation hopes to find stuff needed to make inflation happen so all agree on the motion as well as make the solution stable. Dark energy hopes to find stuff that will make us not like each other. Dark energy, the movie, would be subtitled “The Cosmological Constant, Part 2, The Return of Einstein’s Biggest Mistake.”
[post-posting note: these are three separate areas of study working on distinct problems. The hypotheses are tricky to understand. In particular, the description of dark energy line is not consistent with the predominant view of that issue. These hypotheses are not the focus of this post, so please turn to other sources of information if you are interested in the dominant research efforts.]

As a member of the ultra-conservative fringe, I don’t feel like I can comment on any of these hypotheses.
 I am constrained to work with what I find in my blue PGD (Particle Data Group) Particle Physics Booklet. These are known particles with lots of variables defined. Researchers in the dark arts as I will group them, have reached the conclusion that the dark stuff probably will not be found in the book in my possession. I do wish them luck in the dark arts. I prefer to work in the light where they can take me away. [picture]

Let me define a technical speculation. I will be technical about my definition of a technical speculation, which is:
1. One line of algebra
2. Works with one or less free parameters
A historical example of a technical speculation would be Balmer’s formula of 1885 for the wavelengths of light emitted by hydrogen (more details here). He had 4 pieces of data.

All of the numerators are squares, but they do not make an increasing series. Find equivalent ratios that are an increasing collection of squares:

Good, the numerators are 3², 4², 5², and 6², respectively.
Is there a pattern down below? The denominator is always 4 smaller than what is on top. Here is Balmer’s one line technical speculation:

This has one free parameter h which is 364 nm. This formula was generalized by Rydberg. Bohr’s hydrogen model of the atom justified this formula via quantization of angular momentum with no free parameter. That is how technical speculations progress, from one parameter to none.

Dark matter, inflation, and dark energy are not technical speculations, by this definition. Oops.

Modified Newtonian Dynamics, or MOND, is a technical speculation.
 It was proposed in 1983 by Mordehai Milgrom. The force law for gravity is identical for systems that have a significant amount of acceleration, such as here on Earth. It is only when the acceleration gets eleven orders of magnitude smaller that MOND transforms Newton’s force law like so:

There is one parameter a₀ whose measured value is 1.2 10^-10 m/s². How well does it work? For thin disk galaxies with flat rotation profiles, it has worked like a charm hundreds of times. That is impressive.  Recent studies with gas rich galaxies by Stacy McGaugh showed a nice match for 47 out of 47 such galaxies.

The most important message from the MOND work is that Newton’s law of gravity is hardly broken at all. Things only are off for super-weanie amounts of gravity. It would take an hour and fifteen minutes to fall 1 millimeter. The folks marketing the dark matter hypothesis promote this issue as the huge missing mass problem. All this mass is needed to generate a trivial amount of acceleration. Much press on dark matter stresses it as the only game in town. It is vital to stress the message learned but not embraced by work on MOND:

Newton’s law of gravity is hardly broken at all.

General relativity did a similar thing. The wobbling of Mercury was mostly explained by the other planets (box 40.3 in MTW), some 500 arcseconds per century. Anything that takes a century to add up is not that big an effect. The unexplained part was an order of magnitude smaller, per century. That is what GR fixed. One really needs to be careful in the observations and the calculations to spot this problem. GR does fix the issue. In “Subtle is the Lord...”, the autobiography of Einstein by Pais, he said Einstein was giddy for three days when he realized GR solved this known problem. Good work grand master. A fine example of fine tuning.

By comparison with general relativity, MOND is not pretty. This is one reason it has not been promoted much in the science press. Newton’s inverse square law becomes an inverse distance law when accelerations get small. Something that bothers my eye is the switch to depending not on the mass of the source, but its square root. What is up with that?

Here is the bigger problem: data says MOND is wrong. 
There is the bullet cluster (1E 0657-56), a pair of clusters passing through each other. We can see the stuff, add it all up. We can also measure the speeds and calculate where the gravitational potential is. With the MOND proposal, stuff is stuff. The visual mass and gravitational potential must be exactly aligned. Yet the data says that were we see stuff is not quite where the gravitational potential is.  Oops.

Folks working on dark matter say they are the only game in town now. There is a problem with the transfer of authority. The replacement of the one-parameter MOND technical speculation, must also be a 1/R force law. That is what works with a large body of data. I have yet to see why putting stuff in the numerator as dark matter does should necessarily lead to a 1/R like law when accelerations are small, as the data dictates. Real progress would be to a technical speculation with no free parameters.

Newton’s gravity law has a cause and an effect. I view MOND as really being on the cause side, a 1/R gravity law. What about the effect side of the equation? The effect of gravity is to change momentum. By the product rule of calculus:



Of course all the deltas are changes with respect to time, so we can see our mA. The rocket science term is the constant velocity times the change in mass with respect to time.  How many seconds after the Big Bang lift-off is a system? I have read in papers where people carefully considered the rocket science term. Galaxies don’t throw much matter out, and do not do so quickly. The researchers concluded there is no fuel in a galaxy rocket engine.

Here was my first guess at a relativistic rocket science law for gravity. Keep the cause the same. Use the rocket science term, but give it a relativistic twist, swapping a differential distance over the speed of light c for differential time:



The units are force for all three terms. I showed this to a recent physics Ph.D. friend. He gave it a good, sincere stare, and said that he didn’t think it made sense as a vector equation. I was like, what, that R-hat stuff? After a few days, I decided he was right. Without the right vectors, the above equation is wrong, a bullet to the head. Oops.

Time to make it better. Here is the relativistic rocket science technical speculation: 



There are a few trivial changes. I have made this into a scalar-3-vector or quaternion equation by tacking on the zeros. This indicates the law is conservative, which is true in the classical regime. I have also made the expression dimensionless since nature nurtures naked numbers.

This equation is a technical speculation with no free parameters. It is one better than MOND, progress. It does not alter Newton’s law of gravity at any time or scale. It does provide gravity a new direction to work in, that along the velocity vector. For every system that does not move, like gravity on the Earth, this term is strictly zero. Newton got his apple right. Stuff in a galaxy moves, so the relativistic rocket science effect might come into play.

Where there is no acceleration going on, the force would depend on inverse distance. See the snarky puzzle to show this to yourself.

With two terms on the both sides of the equations, there is no need for both the contributions from Newtonian gravity and relativistic rocket science to exactly line up. It is formally possible to explain the bullet cluster. I am not over-claiming the cards in my hand. I don’t know how to do the calculations involving the bullet cluster. I am only pointing out a possibility.

What we have here is a new classical constant velocity term that involves gravity. Going back to the classical Big Bang, let’s relabel the horizon problem - that all agree on the velocity - the constant velocity problem. Let’s relabel the flatness problem - the fine tuning of initial conditions - the stable solution problem. What classical Big Bang theory needs is a stable, constant velocity solution that involves gravity. That is exactly what the relativistic rocket science term could be. What the data from the cosmic background radiation says is that the only effect of gravity - to 5 significant digits - was the relativistic rocket science term. All were moving at the constant velocity V. The effect of gravity in the Big Bang is to change where stuff is in space. There is no effect of speeding stuff up or slowing stuff down.

As the Universe has aged, we are seeing some sort of shift between these two terms.  Milgrom of MOND fame points out that the expansion acceleration is also super-weanie, one of those ten-to-the-minus ten things.

Balmer had an advantage on me. All he had to do was connect four dots, four numbers. He even predicted two more, not knowing they were already known (he nailed those too). I cannot take computer code already out there and just give the technical speculation a try. That code always cancels the little m on both sides of the equation. Rocket scientists cannot do that. Rocket scientists are smart enough to deal with the challenge. I am not a rocket scientist.

I have spent time and money trying to understand the data going into the rotation profile of a thin disk galaxy, specifically the galaxy NGC3198 in Ursa Major. 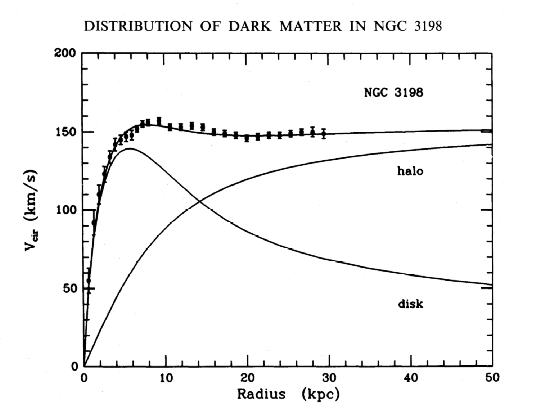So far, it has been beyond my skill set. I have no idea what the numbers that would go into a classical Big Bang calculation or the anomalous acceleration. I am in the deep end of the pool with weights, and my gills receded long ago in the earliest stages of my development.

All I have is a new technical speculation, one line of algebra with no adjustable parameters. That is the rarest of birds in the flock of ideas. Relativistic rocket science is both simple and strange. Like a 6-7-10 split in bowling, it has a chance to knock down three dissimilar problems in astrophysics: galactic motion, the Big Bang, and accelerated expansion.

This result is not new, at least to me. I did a Saturday 8am presentation at a regional APS meeting in the Spring of 2004. I know you were not there, no one but other people presenting their own work was there. But I have sold buttons with the math. Perhaps as many as three over six years.