I have decided to rescind this proposal. Stars in a galaxy travel at one velocity, light at the speed c. There is only one velocity involved in applying the product rule to the definition of a force as a change in momentum. Note that is not a trivial application of the product rule either. Newton's second law is invariant under Galilean transformation. The dm/dt dR/dt is not invariant.
Here are my big picture house rules: no equations in LaTeX or Mathematica. Graphics are allowed so long as they are done by hand. Visually, images break up the monotony of text and provide convenient landmarks. Numbers will be used so long as they are made up, are easy to work with, and are somewhat related to the problem.
Until otherwise notified, presume there is no fusion. All masses are thus constant in time. The word "fusion" does not appear in the index of "Galactic Dynamics", so this assumption does not have an obvious cost other than it makes a galaxy utterly, completely, and profoundly black. I will not be concerned with that detail which would frustrate astronomers.
Constructing a Disk Galaxy
Start with two masses, Big M and small m, where Big M has a mass orders of magnitude larger than small m. Big M effectively stays put while small m travels around in a circular orbit. Kepler spoke the truth long ago that the orbits are really ellipses, but I will work with the assumption that the eccentricities are tiny and not important to the discussions at hand.
What is the functional relationship between Big M and small m? There isn't one. Instead use the Dirac delta function which, despite its name, is really a distribution. One can say either a mass is right there or it isn't there.
The force equation used to calculate the circular velocity was known to Newton himself. It is the solution to the binomial equation where the coefficient of the linear velocity term is zero (b=0, if you memorized the math jingle that starts: "negative b, plus or minus the square root of...").
used to calculate the circular velocity was known to Newton himself. It is the solution to the binomial equation where the coefficient of the linear velocity term is zero (b=0, if you memorized the math jingle that starts: "negative b, plus or minus the square root of...").
Now work with three masses in a row. One Big M and two small m's to either side. The delta function is still used to describe the situation.
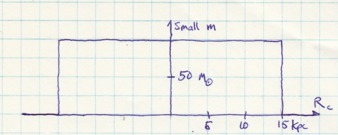 Now work with a continuous line of masses. Spread them out over 30 kpc. Let there be 100 solar masses per kpc for a total of 3000 solar masses. That is Big M. For a force calculation, one doesn't work with Big M directly. Instead one sums up all the small m's, more specifically one sums up the ratio of small m masses over the square of the distances. The size of small m depends on the width of the slice taken from the line of masses. If the slice was a hundredth of a kpc, small m would be a solar mass.
Now work with a continuous line of masses. Spread them out over 30 kpc. Let there be 100 solar masses per kpc for a total of 3000 solar masses. That is Big M. For a force calculation, one doesn't work with Big M directly. Instead one sums up all the small m's, more specifically one sums up the ratio of small m masses over the square of the distances. The size of small m depends on the width of the slice taken from the line of masses. If the slice was a hundredth of a kpc, small m would be a solar mass.
Mass and distance now have a functional relationship: it is constant, always 100 solar masses per kpc. This kind of straight line with a constant mass per kpc ratio is not seen in Nature. Why? Apparently it is not a stable solution to galactic dynamics.
One error I made in my previous blog was to keep thinking in terms of Big M, small m and even fusion m. Once there is a way to write m as a function of distance, that is really all there is. What was Big M is merely a sum of all the small m's over a range of distances. That particular sum is not particularly important as it is just a characteristic of the system. What is important is the gravitational field which is a sum of small m masses over distances taking into account the geometry of the system. I will be focusing on the small m's from now on because they are in motion and can be used in calculating the gravitational field given the function and distance from the center of the galaxy.
Now imagine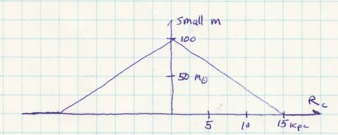 a straight line of masses that starts from nothing and rises linearly to 100 solar masses in 15 kpc, then falls back linearly at the same rate. The total mass is 1500 solar masses. Go out 7.5 kpc from the center, and the solar masses per kpc is 50. The slope is no longer zero, but is constant. This simple model is not seen in Nature.
a straight line of masses that starts from nothing and rises linearly to 100 solar masses in 15 kpc, then falls back linearly at the same rate. The total mass is 1500 solar masses. Go out 7.5 kpc from the center, and the solar masses per kpc is 50. The slope is no longer zero, but is constant. This simple model is not seen in Nature.
Now use 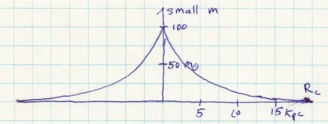 an exponential decay for the mass as a function of distance. What matters for an exponential decay function is the length scale, call it Rd. The exponent must be dimensionless, so one uses the distance from the center, Rc, over the length scale to generate a dimensionless number, Rc/Rd. The mass drops off quickly for a small length scale. The numbers drift down slower for a large length scale. I will use a length scale of 5 kpc because that is seen sometimes in Nature. A little quality time with a calculator leads to this table of numbers:
an exponential decay for the mass as a function of distance. What matters for an exponential decay function is the length scale, call it Rd. The exponent must be dimensionless, so one uses the distance from the center, Rc, over the length scale to generate a dimensionless number, Rc/Rd. The mass drops off quickly for a small length scale. The numbers drift down slower for a large length scale. I will use a length scale of 5 kpc because that is seen sometimes in Nature. A little quality time with a calculator leads to this table of numbers:
| Rc | Rc/Rd | m |
| 0 | 0 | 100 |
| 5 | 1 | 100 e-1 ~ 36 |
| 15 | 3 | 100 e-3 ~ 5 |
There is nothing special about these numbers. I like being concrete even in this abstract domain. Notice that I used small m because Big M is the sum of all these small m's.
I am not familiar with the vast collection of galaxies found in technical star catalogues. I believe a "straight as uncooked spaghetti" galaxy is rare. Cook the spaghetti. Toss it on a counter and give it a slight twist in the center. A gentle "s" curve will form. This shape is seen quite often as a bar galaxy. I checked with "Galactic Dynamics", and there are bar galaxies with an exponential decay of luminosity with distance. Superposition a bunch of s curves and one gets a disk galaxy. The mass will decrease exponentially for each strand of spaghetti, but now an area is covered.

A galaxy is stable over long periods of time. Mass densities are low. Motion is slow relative to the speed of light. Gravity is weak. The spatial scale is H U G E. A galaxy is as classical as a classical system can be. There is no need for the tools of relativity and quantum mechanics.
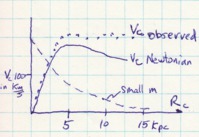 Newton's law of gravity when applied to a disk galaxy works at the start up to the peak, but fails for the tail of a velocity profile. Newtonian theory demands the velocity falls off, yet it often stays at the peak velocity. A velocity profile of a classical system should be an easy problem even if the math details for the gravitational potential are a bit scary. The velocity profile of a disk galaxy is a current problem that demands fixing. Let's take a big picture view of two proposals to fix the problem.
Newton's law of gravity when applied to a disk galaxy works at the start up to the peak, but fails for the tail of a velocity profile. Newtonian theory demands the velocity falls off, yet it often stays at the peak velocity. A velocity profile of a classical system should be an easy problem even if the math details for the gravitational potential are a bit scary. The velocity profile of a disk galaxy is a current problem that demands fixing. Let's take a big picture view of two proposals to fix the problem.
MOND (Modification Of Newtonian Dynamics)
As an equation and data guy, I have professed in the comments section of other blogs an affinity for the ability of MOND to match the velocity profile of a hundred or so disk galaxies. I like the message that MOND only comes into play when gravity is trivial, some ten orders of magnitude smaller than on the surface of the Earth. That suggests we need a minor fix of some sort.
In this blog, I have my big picture hat on, and the view is not pretty. MOND claims that one sails out from the center of the galaxy feeling the one over distance squared force of gravity. The start could not be more reasonable. Then at some distance where gravity happens to be feeble - say 3 kpc - the form of the law changes to a one over distance force law. That is not reasonable. Is there any other fundamental force law like this? Being an inverse square law is essential for gravity to be a long range force. Gauss's law works for the core, but not for larger radii where the one over distance law prevails. This changes the unlimited reach of gravity: (hyperphysics).
Any point source which spreads its influence equally in all directions without a limit to its range will obey the inverse square law. This comes from strictly geometrical considerations. The intensity of the influence at any given radius r is the source strength divided by the area of the sphere. Being strictly geometric in its origin, the inverse square law applies to diverse phenomena. Point sources of gravitational force, electric field, light, sound or radiation obey the inverse square law. [emphasis added by me]
This strikes me as a big picture deal breaker. Gravity is one of two fundamental forces with unlimited reach, and the only one that really shapes the cosmos. If a galaxy has switched over to a one over distance force law to get the outer velocity profile correct, what does that imply for the interaction between two galaxies which would be even greater distances and weaker gravity?
What about the Lagrangian? David Halliday had some thoughts on the subject, so read his stuff here (you can skip my comments :-) There are a few major technical roadblocks in the way of accepting one of the relativistic Lagrangians as being reasonable. I won't go into that swamp now. The big picture view is that at the Lagrangian level, the change from general relativity to a relativistic form of MOND is a challenge.
Dark Matter
At the Lagrangian level, the dark matter proposal creates a mystery mass term twin. There is the matter seen and measured in a telescope using one conversion factor, a mass to light ratio. For the dark matter proposal, add in a no-see-'em mass that arises only out of calculations adjusted until the model fits the data. This sounds too much like ballot stuffing where we do not even know what the stuffing is made of. This fix usually requires more dark matter than visible matter, so the fix for the problem is huge. I have seen physicists I profoundly admire serve up the dark pie graph. It makes me feel unwell.
Let me provide one detail that turns my stomach. A thin disk galaxy is pulled together under the forces of self-gravitation. One might expect dark matter is added to the disk so that the model fits the rotation profile. But that does not solve a less well-known problem: the stability of the disk to perturbations. With only normal matter, a disk galaxy that gets a tiny nudge from a passing galaxy should curl up and collapse. The modellers speculate that the dark matter is distributed in a sphere so that the visible matter disk is stable. I am confident the spherical distribution of dark matter solves the stability problem. Yet it creates a physics problem: both the visible and dark matter follow different roads in the self-gravitation process to create different shapes. I am skeptical.
The Ultra-Orthodox Fringe
In my first blog at Sceince20.com, I defined a credo I called "The Ultra-Conservative Fringe". I think I have been faithful to that credo. While I still have a scientific belief that gravity must be unified elegantly with the rest of physics, including quantum mechanics, my own GEM unification proposal was wrong and I do not have a new concrete proposal worth anyone's time. I have tried to do a number of different things, but those efforts came up short. Time to adjust the credo.
Let me define a new label, "The Ultra-Orthodox Fringe". Here again is my definition of fringe which can be applied without judgement:
I define the fringe as anyone trying to make a contribution to a field where they are not employed or do not have a degree in the subject.
By this definition, I remain a fringe physicist. To be ultra-orthodox, one can only work with widely used and accepted Lagrangians. Add anything new to a Lagrangian and it is a safe bet the addition does something bad. This does limit creativity in physics, but such is the burden of the label. The second principle is that only unstated assumptions can be challenged. Assumptions that get examined in introductory textbooks are presumed to be in fine shape given the many hours graduate students have spent going through the details.
Unstated assumptions, by their nature, are hard to find. There is no more weekly blogging for me. If such an assumption is found, I will not treat it cavalierly, "Oh, I am sure that has been done before." I still retain my goal of debunking my own work. Debunking also requires effort, hence my weeks of silence on this subject. Thinking and refining thinking takes time.
The Light Matter Proposal
The light matter proposal is an effort to examine the effect of fusion and its gravitational mass change in time on the rotation profile of thin disk galaxies. The light matter proposal does not alter the Newtonian gravity scalar field Lagrangian. The formal solutions must be the same. How could the light matter proposal be any different from the standard approach? The circular velocity is the solution to the binomial equation where b - the coefficient next to the linear velocity term - equals zero. This is the unstated assumption: for a system undergoing fusion, treat the change in mass per time as exactly zero even though the mass does change in time based on the physics of fusion. I could find no references to fusion and the way mass changes in time in two of Alar Toomre's papers from the early 60s, nor in the modern textbook "Galactic Dynamics" by Binney and Tremaine. I will proceed to examine this unstated assumption.
I can imagine others not lifting a pencil because galaxies are stable over long periods of time. One needs a static equation for the velocity profile, one that has no time dependence what-so-ever. Either the derivative of mass with respect to time will be zero as everyone assumes, or it will not be zero and thus not be part of a static solution.
With no fusion, the derivative of the mass with respect to time is zero. Every small m mass changes in time in the same way: the change is equal to zero. It is possible that every small mass m changes in time in the same way but that same way is not zero. Only in that case could one have a dynamic, time-dependent force equation where, due to the cancellation of the time-dependent small m terms, the circular velocity would be static.
Now turn on fusion.
Fusion uses an isotropic conversion of mass to do two things: mostly to keep a star burning and secondarily to sent photons to all corners of the Universe.
Fusion is caused by gravity gathering together copious quantities of hydrogen in one location. Gather so many kilograms of gas that somewhere near its core in an act of quantum tunneling, two hydrogen atoms fuse to make one helium atom. Ignition leads to more fusion. The initial work of fusion is to warm up the huge mass of gas. Eventually the star will reach a steady state, with the core at 5 million degrees but the surface at a mere 5 thousand, a difference of four orders of magnitude. In steady state mode, most of the energy of fusion remains with the star, and thus remains as part of the star's gravitational field which is made up of all forms of energy. Note that is a quality of general relativity. Only a tiny amount of fusion energy escapes in all directions to light the heavens. Only the energy that escapes can contribute to the change in mass per unit time term.
The amount of mass converted to energy in a star every second is non-zero and trivial, roughly twenty orders of magnitude smaller than the mass of a star. Imagine running and having one cell fall off each second. Do you think your race time will be changed? A cell is on the order of 10 times greater than the mass loss per second for fusion. The person who learns to shed cells is not going to alter their race times in any material way. In the same way, the momentum change due to fusion is trivial.
The mystery being investigated is the circular velocity. The binomial equation is used to solve for the circular velocity. Fusion matters because it makes the coefficient of the b term with the linear velocity no longer equal to zero while fusion is on. Change the coefficient b from zero, and that necessarily changes the velocity profile curve.
The amount of fusion happening in a star is a function of a galaxy's age. Extremely young and old galaxies look the same: complete blackness, no fusion. Between those two periods of darkness is the light phase. The coupling term I introduced is needed to characterize the amount of light that escapes the galaxy over the amount of fusion energy that stays with the galaxy. For the extremely young and old, no light is being generated, so it is zero. When galaxies are producing light, a sliver of which is leaving, then the coupling term is not zero.
It is vital to think about the two terms in the standard velocity profile equation. One is for the force of gravity, the other is the effect of centripetal acceleration. Both terms depend on the radial distance R. To be pedantic, R is the distance from the center of a disk galaxy out to the distance where one will calculate the circular velocity. Thus the distances used in the equations are not something general. Use the symbol Rc to indicate the distances start from the center of the disk and increase. The symbol Rc behaves like any other distance in an equation, but the subscript c indicates the center of the galaxy is the origin of the model used.
The third term I am exploring arises from the product rule of calculus and the centripetal force. It must share the property of being a description of the galactic system from the center as one goes out. Yet the new term is a derivative with respect to time. How could time have anything to do with the geometry of the galaxy? Because Nature is logically consistent, use precisely the same model for time, tc. It is the time needed to travel from the center of the galaxy out to different radii. The time tc behaves like any other time, but one is constrained by the model for time that represents going from the center of the galaxy on out because the circular symmetry makes calculations easier. To apply the product rule to the same small mass m at a distance 5 kpc from the center, use the distance Rc=5kpc and the time tc=5kpc/c.
What does it mean to shift from two to three terms? A force equation is a cause and a matching effect. In MOND and dark matter, the cause is changed dramatically. In the light matter proposal, the cause is unaltered. Instead the effect of gravity is distributed into two effects: the centripetal force and the isotropic mass loss term. The centripetal force will dominate for small radii, while the isotrophic mass loss term takes over for large radii.
Let's see the isotropic mass loss in action. Fusion happens everywhere there are stars in a galaxy. Certainly more fusion will happen at the center than at the edge. I need to pick a non-zero coupling factor, the ratio of energy leaving the galaxy to let us know about the galaxy over the energy that stays with the galaxy. Let's say it is one part in a hundred. The amount of fusion going on at a particular location must go in step with the small m mass at that location:
| Rc = c tc | Rc/Rd = c tc/Rd | m | γm |
| 0 | 0 | 100 | 1.00 |
| 5 | 1 | 100 e-1 ~ 36 | 0.36 |
| 15 | 3 | 100 e-3 ~ 5 | 0.05 |
The amount of mass available to undergo fusion has the same exponential decay and length scale as the small m mass. The mass change in time exponential needs a time scale that is directly related to the mass scale, which would be Rd/c. It is the exponential mass distribution which "powers" the constant velocity, mass change in time effect.
The b term in the binomial equation for circular velocity is the linear velocity times a derivative of mass with respect to time. A common first reaction is to ignore this oddball. It doesn't matter how extensive your career in physics happens to be: you have done no calculations with isotropic mass change, ever. Rocket scientist deal with mass loss in a particular direction. The only system that has isotropic mass change is a system undergoing fusion. The only people who might do such work, from Alar Toomre to Binney and Tremaine, have not made any effort to do such a calculation readily available.
I showed a draft of this blog to a friend, and he wondered about the rotation profile data coming from hydrogen gas spectral lines, gas that is in between stars and definitely not undergoing fusion. The mass of the gas is still part of small m, all the mass that happens to be at a particular place relative to the center of the galaxy. The hydrogen gas and any stars are all fed into the same binomial equation for the circular velocity. The gas is part of the cause. The gas is part of the centripetal effect. And I have argued here that as part of small m, it still plays a role in the time dependent term as seen in the table above.
My Own Big Picture
By the ultra-orthodox fringe credo, I cannot work on MOND, they play seriously odd games with the Lagrangian. I cannot join those playing equation games with dark matter to make a perfect match to a velocity curve depending on the whim of my model. My lack of participation is of no consequence to those projects, and I wish them luck.
I cannot say the product rule of calculus doesn't work in this case. I cannot say the solution to the binomial equation doesn't come into play.
Still, how could such a small mass involved in fusion have such a big effect? What is not small is going from two terms in solving an equation to three terms. That third term has an unusual linear dependence on the circular velocity. What is relevant is not the amount of fusion, but the time scale because it is the terms in the exponent of the exponential that come down in the derivative and live on for the circular velocity.
This blog failed for two reasons. First, I didn't find a flaw in my refined big picture review. My goal is to debunk the light matter proposal so I can give up the ultra-orthodox shackles and go out partying weeknights after I put the little girl to bed. The second shortcoming is a limitation of the big picture approach. If the solution to a binomial equation goes from two terms to three, how does the velocity profile actually change? Does the change look like the data? I did not write my previous blog until I saw a graph that was consistent with the data. You can look at the equations and graphs in that blog, but skip over most of the discussion as it has evolved quite a bit since then.
COMMENT NOTE: I will delete comments from anyone who does not log into the site, whether positive or negative. It is a simple rule to enforce and easier on my constitution as anonymity lends to less respectful replies. The comment must also have some physics easy to connect to the blog at hand or it too will be deleted. Those are my house rules.



Comments