[note: this blog, as written is insufficient. I will need to provide an action to clarify the nature of the proposal.]
The Spoon and the Moon
Give a baby a spoon, and the little one is likely to toss it to the floor, greatly amused. Return the spoon and the baby will gleefully demonstrate that the experiment can be repeated.
The Moon falls around the Earth. The Moon has not stopped falling toward the Earth for four billion years. It may be the greatest accomplishment of abstract scientific thought that the same law that governs the spoon falling also governs the motion of the Moon. Newton's Universal Law of Gravitation was the first expression which established that the same law works in the heavens as it does on Earth. Here is that law:
The small m could be the mass of the spoon or the Moon. Notice it appears on both sides. Written on the left, the mass times acceleration is an inertial mass, a resistance to change. The spoon is easier to move around than the Moon. On the right, there is a minus sign which indicates the force is attractive. The gravitational attraction of the small m to the big M (Earth) must be divided by the distance squared. The gravitational constant G is there so that the expression has units of force.
The inertial mass m happens to be the same as the gravitational mass m. In perhaps the second greatest accomplishment of abstract scientific thought, Einstein used that equivalence to construct his theory of gravity. I will not try to explain that idea in any detail other than to say it is about dynamic space-time geometry, where something is in a gravity field changes measurements of both time and space. General relativity is like a sublime wine, the more opportunities one gets to study the subject in detail, the more giddy one gets with its elegance.
The Problem with Light
The effect of gravity is universal. Gravity even tugs light. Watching the position of the stars during an eclipse gave the first data that the path light of the heavens is altered by the mass of the Sun. Using radio astronomy, it was possible to study light bending at any time of the year. All the data that poured in was consistent with the predictions of Einstein's approach to gravity, general relativity.
There is a problem with Newton's Universal Law of Gravity written down by Sir Isaac himself. The mass of a photon is zero. The law applied to photons says zero equals zero. While true, it is no use for doing a calculation. Physicist know to use general relativity. Yet I think one should give the father of physics more respect. Is there an upgrade one could apply to this grand old law?
Upgrading the Law
Why not replace the mass of the spoon or the Moon on either side with universal constants? There is a combination of such constants known as the Planck mass (the weight of a flea egg according to wikipedia). Let that be a stand in:
A photon with a mass of zero will not be a problem for this law. The upgrade make's Newton's law more universal because it can also be used to describe the motion of light.
Physicists have already calculated how much Newton's theory predicts light bends in the limit of the mass approaching zero. The theory gets half the amount seen. This upgraded gravity law remains inconsistent with experimental data and so remains wrong.
The upgrade is interesting for a number of reasons. The law now looks like it is only about geometry [note to the technical reader: out of habit, I wrote "space-time geometry", but that is not right since this upgraded law remains fixed to Galilean geometry]. On the left are a few constants and an acceleration, the change in the change of space per unit time. Upgrading Newton's theory shows respect for the accomplishments of general relativity: gravity is only about geometry (albeit the wrong geometry).
General relativity was born from a careful analysis of the equivalence of inertial and gravitational mass. Now neither is in the equation. Interesting.
Newton's original equation had one constant, G, whose value was not known to Newton. The presence of the Newton's gravitational constant indicates the equation is related to gravity. The field equations that make up general relativity have the constants G and c, the speed of light. This indicates the equations touch on gravity and special relativity. The upgraded gravity law brings in a third constant, Planck's constant, hbar. That is the calling card of quantum mechanics. On dimensional grounds, the upgraded law looks like its domain of application should be relativistic quantum gravity, the driver of so much research today. I am NOT claiming to have a full blown quantum gravity model. I don't even have a toy model. I think this is worthy of more investigation, and that's about it.
The solution to the field equations
Field equations go hand in glove with the equations of motion. The classical field equations gravity look like so:
The solution for a point charge is:
There are two integration constants because this is a second order differential equation. Take two spatial derivatives of M/R and the units are mass per volume, so k is dimensionless. Is k positive or negative? The force equation must be attractive:
[note: out of habit, I started to write "like charges attract", but realized with the upgrade to Newton's law proposed here, there was only the gravitational mass. Getting rid of a cliché phrase, how fun is that?]
A spatial derivative of M/R will bring in one minus sign, so k must be negative so that the three negative signs end up staying negative, and the force is attractive.
The negative k creates a problem: the field has a negative energy. The problem can be avoided if the additive constant C is HUGE. Making certain the energy of the gravitational field was positive definite was a problem that bothered James Clark Maxwell (see an excellent page devoted to the subject written by Kevin Brown). Maxwell was unable to justify creating such a huge positive value. In general relativity, the metric term g00 is one minus a super-small M/R term due to the constants G/c2, a small number divided by the square of a large number. Use the inverse of those same constants to make the energy in the field positive definite but the gradient negative:
It is quite common for people to ignore the additive constant. Yet it does solve a problem the perplexed Maxwell, so is worthy of noting.
Limits to the Upgrade
Newton's universal law of gravitation is now more universal because it applies equally well to spoons, moons, and photons. Just because it applies to photons does not mean it gets the answer right: it is off by a factor of two. On a deeper level, the upgrade does not make Newton's gravitational law about space-time geometry. Space remains separate from time via Galilean transformations. The speed of light is still infinite according to the field equations. Newton's gravity law only changes time, not space, and again not consistent with data. Wrong, wrong, wrong.
The upgrade is interesting to me. I've been saying that like charges attract since I first learned of gravity. Now I cannot say that. Gravity is not about charges in upgraded Newtonian theory which is a good thing.
I can no longer write the Universal Law of Gravity as Newton did at the dawn of the modern scientific process without seeing the photon zero equals zero blunder. Wrong is wrong. Unless I am wrong about the upgrade to the oldest gravity law on the books.
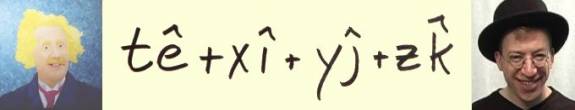




Comments